
De Pasterski–Strominger–Zhiboedov-driehoek (PSZ-driehoek), vernoemd naar de natuurkundigen Sabrina Gonzalez Pasterski, Andrew Strominger en Alexander Zhiboedov, is een drietal relaties tussen ideeën uit verschillende gebieden van de natuurkunde: deeltjesfysica, astrofysica en ‘formele’ relativiteitstheorie – de tak van de mathematische fysica die zich bezighoudt met de wiskunde van de algemene relativiteitstheorie. De relaties verbinden fenomenen die optreden bij lage energie, en de PSZ-driehoek wordt in natuurkundetaal dan ook de infrarooddriehoek genoemd. Infrarode golven hebben immers een relatief lange golflengte – in tegenstelling tot ultraviolette golven – en dus lage energie. Wat zijn de drie fenomenen in de infrarooddriehoek en hoe zijn ze aan elkaar gerelateerd?
Symmetrieën aan de rand van het universum
De eerste hoek van de PSZ-driehoek wordt gevormd door asymptotische symmetrieën. Zoals al vaker is besproken op de Quantum Universe-website (bijvoorbeeld in dit artikel), wordt met ‘symmetrie’ bedoeld dat de uitkomsten van natuurkundige experimenten gelijk blijven als we bepaalde transformaties op het systeem uitvoeren. Het maakt voor de uitkomsten bijvoorbeeld niet uit wáár we een experiment uitvoeren (translatiesymmetrie) of wannéér we het experiment uitvoeren (tijdtranslatiesymmetrie). Emmy Noether bewees dat iedere symmetrie samengaat met een behouden grootheid, een resultaat dat nu bekend staat als de Tweede Stelling van Noether. Translatiesymmetrie leidt bijvoorbeeld tot behoud van impuls, en tijdtranslatiesymmetrie resulteert in behoud van energie. Belangrijk om hierbij op te merken is dat Noethers stelling het dus mogelijk maakt een nette wiskundige definitie van grootheden als ‘impuls’ en ‘energie’ te geven, namelijk als de behouden grootheden die horen bij bepaalde symmetrieën.
In de algemene relativiteitstheorie blijven de symmetrieën die we kennen uit ons dagelijks leven niet overeind: ruimte en tijd, versmolten tot een ‘ruimtetijd’, worden vervormd door de aanwezigheid van objecten met massa. Hierdoor is er geen eenduidige definitie meer van ‘afstand’ en ‘tijd’, en is er dus al zeker geen translatie- of tijdtranslatiesymmetrie. Maar als er geen (tijd-)translatiesymmetrie meer is, hoe definieer je dan energie of impuls? Een mogelijke oplossing voor dit probleem is om deze grootheden te definiëren door de ruimtetijd heel ver weg van alle verstoringen – aan de ‘rand’ van het universum – te beschouwen, zodat het net lijkt alsof er helemaal geen verstoringen zijn. Denk bijvoorbeeld aan een grote trampoline met een persoon in het midden: in de buurt van de persoon zal het trampolinedoek weliswaar vervormen, maar aan de rand zal het doek er bijna hetzelfde uitzien als wanneer er geen bal was geweest.

De asymptotische symmetrieën zijn de symmetrieën van de ruimtetijd oneindig ver weg van alle massa’s. In de praktijk is het niet mogelijk om écht oneindig ver ergens vandaan te gaan, maar we kunnen wel dat wat er ‘heel ver weg’ gebeurt wiskundig extrapoleren naar wat er op oneindig grote afstand zou gebeuren. Op basis van het trampoline-voorbeeld verwacht je misschien dat de asymptotische symmetrieën gelijk zijn aan de symmetrieën van een lege ruimtetijd (de Poincaré-symmetrieën), en dat er dus in het bijzonder weer (tijd-)translatiesymmetrie is. In 1962 bewezen natuurkundigen Bondi, Metzner en Sachs (BMS) dat dit inderdaad het geval is, maar dat er daarnaast nog een extra verzameling van symmetrieën is. Deze BMS-symmetrieën worden ook wel – ietwat ongelukkig – supertranslaties genoemd: het voorvoegsel ‘super’ slaat op het feit dat de Poincaré-symmetrieën bevat zijn in de verzameling van BMS-symmetrieën, maar heeft niets te maken met de veelbesproken supersymmetrie.
Zachte stellingen
De tweede van de drie fenomenen in de PSZ-driehoek heeft te maken met botsingen van elementaire deeltjes. Zo’n botsing zorgt ervoor dat deeltjes van richting veranderen of zelfs dat de oorspronkelijke deeltjes transformeren in nieuwe deeltjes. Deze verschijnselen worden verstrooiing genoemd. De term ‘botsing’ is ietwat misleidend, omdat de deeltjes elkaar niet aan hoeven te raken om invloed op elkaar uit te kunnen oefenen. Een bekend voorbeeld van een botsing is de onderlinge afstoting van twee elektronen: wanneer twee elektronen bij elkaar in de buurt komen, zorgen hun elektrische velden ervoor dat ze weer uit elkaar worden geduwd.
Wanneer een aantal deeltjes op elkaar botst, zijn er in het algemeen verschillende resultaten mogelijk. Om de kans op één specifiek resultaat te berekenen, wordt gebruik gemaakt van verstrooiingsamplitudes. In wiskundige termen zijn dit complexe getallen die je kunt uitrekenen als je de eigenschappen van de inkomende en de uitgaande deeltjes van de botsing weet. De kans op een specifieke uitkomst, gegeven de inkomende deeltjes, is gelijk aan de grootte van de verstrooiingsamplitude in het kwadraat. Het berekenen van steeds ingewikkeldere verstrooiingsamplitudes is een belangrijk onderdeel van de deeltjesfysica. Je kunt je waarschijnlijk wel voorstellen dat het moeilijker wordt om een verstrooiingsamplitude uit te rekenen als er meer deeltjes betrokken zijn bij de verstrooiing. Om de berekeningen te vereenvoudigen wordt gebruik gemaakt van verschillende technieken, waaronder zachte stellingen. Deze zachte stellingen geven relaties tussen de verstrooiingsamplitudes van bepaalde processen en de verstrooiingsamplitudes van processen die er heel erg op lijken, maar met een aantal deeltjes minder. De term ‘zacht’ verwijst hierbij naar de energie van de weggelaten deeltjes, die veel lager moet zijn dan de energie van de deeltjes die overblijven.
Een belangrijk voorbeeld van een zachte stelling die natuurkundigen veel gebruiken is de zachtegravitonstelling. Deze stelling beschrijft verstrooiingsamplitudes van botsingen waarbij gravitonen – de deeltjes die zwaartekracht overbrengen – betrokken zijn. Stel dat een bepaalde botsing van n inkomende deeltjes resulteert in m uitgaande deeltjes, en dat dit proces beschreven wordt door een verstrooiingsamplitude met waarde A. Als we nu hetzelfde proces bekijken, maar mét een extra graviton met lage energie, dat wordt opgenomen of uitgezonden door een van de inkomende of uitgaande deeltjes, dan zegt de zachtegravitonstelling dat de verstrooiingsamplitude A’ van dit nieuwe proces gerelateerd is aan de verstrooiingsamplitude A van het oorspronkelijke proces. Om preciezer te zijn is de amplitude A’ (met graviton) gelijk aan de amplitude A (zonder graviton), vermenigvuldigd met een factor die alleen afhangt van de impuls van het graviton en het deeltje waar het een interactie mee heeft. Dit technische verhaal is geïllustreerd in onderstaande afbeelding.
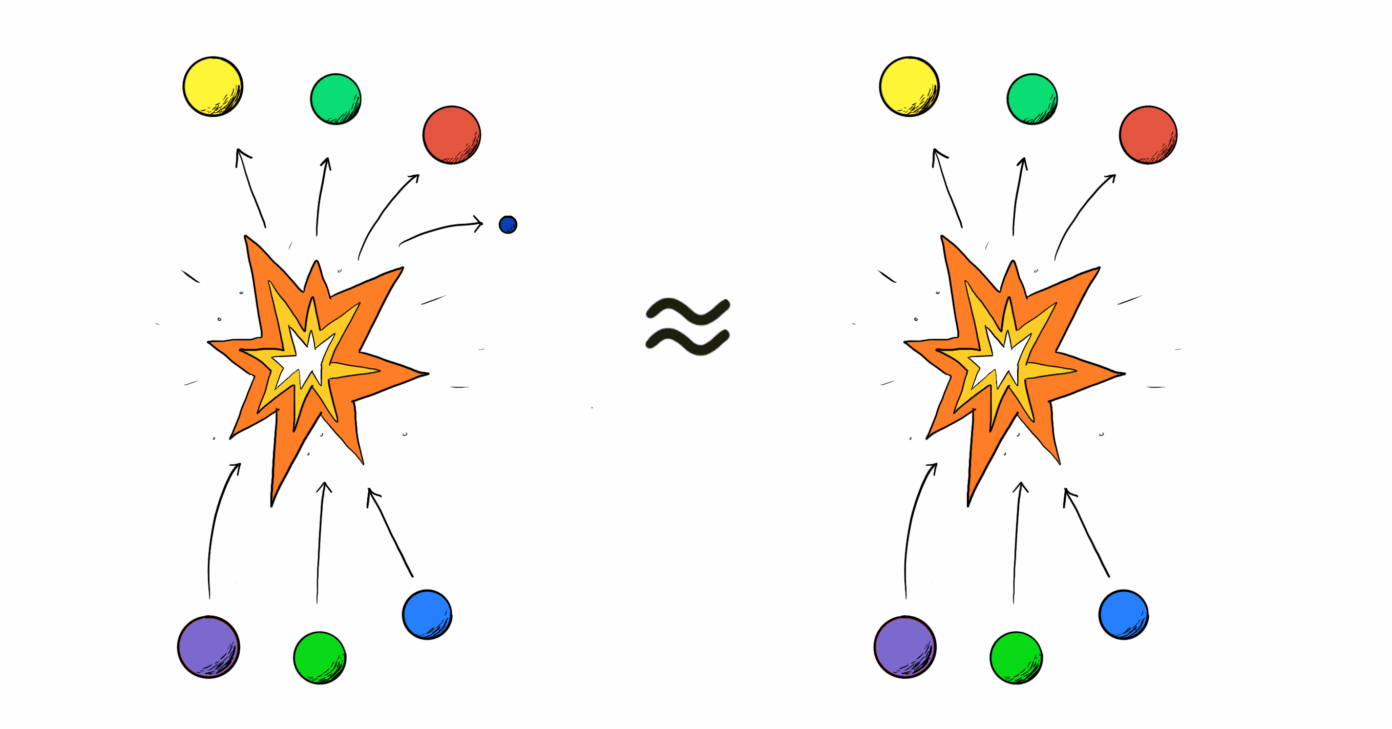
De zachtegravitonstelling is dus een hulpmiddel dat het makkelijker maakt om verstrooiingsamplitudes uit te rekenen van botsingen waarbij een graviton met lage energie betrokken is. Naast de zachtegravitonstelling bestaat ook de zachtefotonstelling, die hetzelfde werkt als hierboven beschreven, maar dan met een foton – een lichtdeeltje – in plaats van een graviton als extra deeltje. Daarnaast wordt er onderzoek gedaan naar, onder andere, zachte stellingen voor botsingen waarbij twee of meer deeltjes met lage energie betrokken zijn, zachte stellingen in theorieën met supersymmetrie en zachte stellingen in de snaartheorie.
Het geheugeneffect
Het derde en laatste fenomeen uit de PSZ-driehoek is het geheugeneffect. Dit fenomeen heeft te maken met zwaartekrachtsgolven, rimpelingen van de ruimtetijd die veroorzaakt worden doordat bewegende massa’s van snelheid of richting veranderen. De algemene relativiteitstheorie voorspelt dat de zwaartekrachtsgolven een blijvende vervorming van de ruimtetijd veroorzaken, bijvoorbeeld in de vorm van een permanente verplaatsing van objecten – het verschuivingsgeheugeneffect. In het bijzonder zou het geheugeneffect zich kunnen uiten in een permanente verplaatsing van de spiegels in een zwaartekrachtsgolvendetector zoals LIGO. Zoals ik eerder al uitlegde in dit artikel, is het geheugeneffect nog niet waargenomen, maar is er goede hoop dat dit in de toekomst wel gaat gebeuren met de LISA-detector.
Drie hoeken maken nog geen driehoek
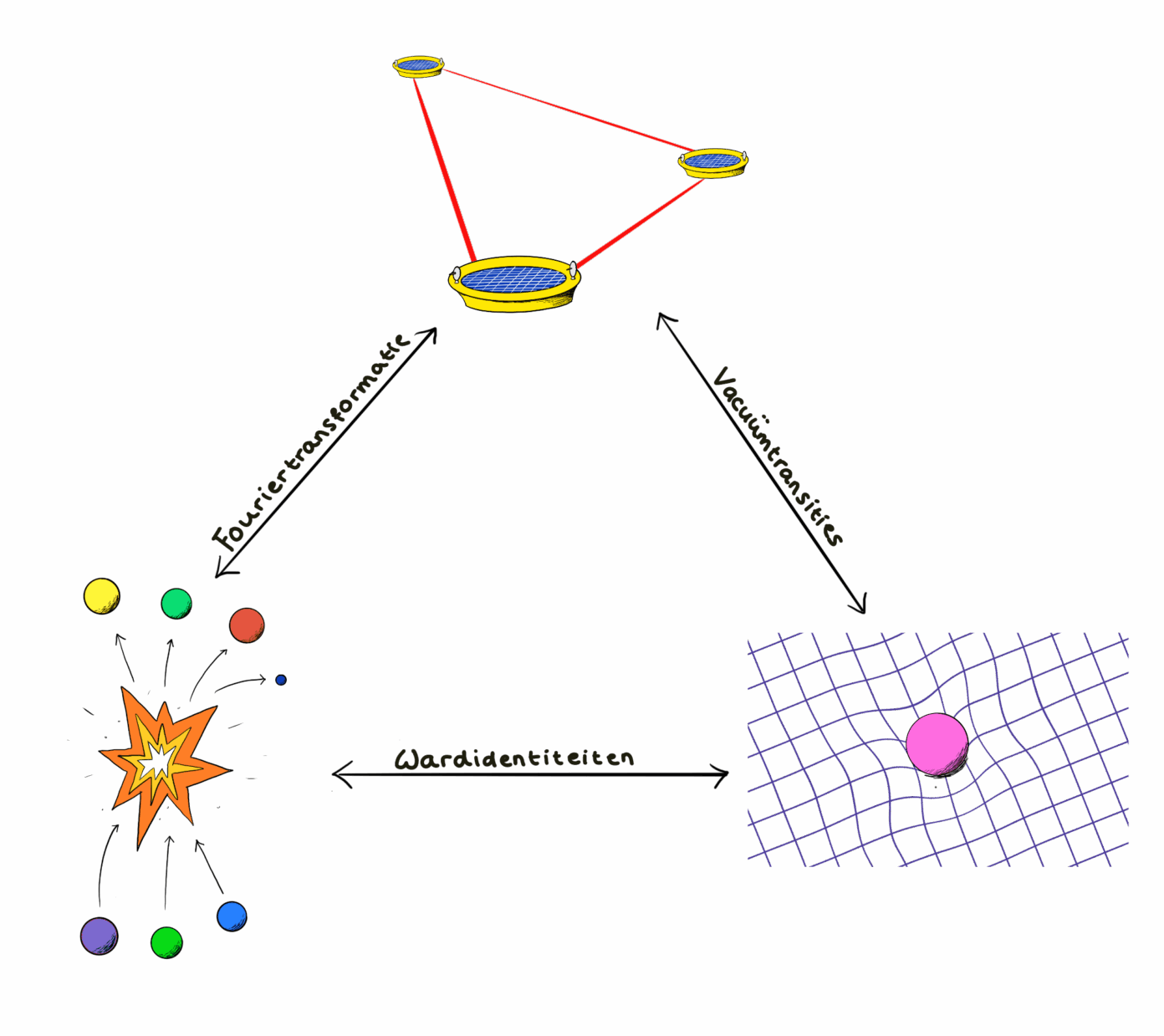
Op dit punt begin je je misschien af te vragen wat de hierboven besproken onderwerpen met elkaar te maken hebben. Zo’n tien jaar geleden bewezen Andrew Strominger en zijn collega’s dat de fenomenen met elkaar verbonden zijn door een drietal wiskundige relaties. Misschien wel de eenvoudigste (maar nog steeds vrij abstracte) van de drie relaties is die tussen zachte stellingen en het geheugeneffect. Deze fenomenen zijn aan elkaar gerelateerd door middel van een wiskundige operatie die bekend staat als de Fouriertransformatie. We zagen eerder in dit artikel dat de verstrooiingsamplitudes in zachte stellingen aan elkaar gerelateerd zijn door vermenigvuldiging met een factor die afhangt van de impulsen van de betrokken deeltjes. Voor de zachtegravitonstelling blijkt dat de Fouriertransformatie van deze factor gelijk is aan een functie die een verschuiving van de posities van de betrokken deeltjes beschrijft. Dit is precies in overeenstemming met de verschuiving van objecten die optreedt in het verschuivingsgeheugeneffect.
De zachte stellingen zijn ook gerelateerd aan asymptotische symmetrieën, en wel door een soort quantummechanische versie van de Tweede Stelling van Noether. Zoals eerder in dit artikel al aangestipt, vertelt Noethers stelling ons dat er voor elke symmetrie een behouden grootheid is. Dit resultaat is correct op klassieke (alledaagse) schaal, maar in de quantummechanica wordt de natuur beschreven in termen van kansprocessen, en dus zijn er enkele kleine aanpassingen van de stelling nodig. Deze aanpassingen, waarvan de wiskundige ingrediënten bekend staan als de Wardidentiteiten, zeggen grofweg dat de kans op bepaalde gebeurtenissen zó is dat het in overeenstemming is met behoud van grootheden zoals voorspeld door de stelling van Noether. Je kunt hierbij bijvoorbeeld denken aan de kansen op bepaalde verstrooiingsprocessen van elementaire deeltjes, die zodanig zijn dat ze in overeenstemming zijn met behoud van elektrische lading. We zagen eerder dat zulke kansen beschreven worden door de verstrooiingsamplitudes. Het blijkt dat de zachtegravitonstellingen voor verstrooiingsamplitudes precies gelijk zijn aan de Wardidentiteiten die horen bij de asymptotische symmetrieën van Bondi, Metzner en Sachs.
De driehoek wordt afgemaakt door de relatie tussen asymptotische symmetrieën en het geheugeneffect. Om deze relatie te kunnen begrijpen, moeten we weten wat er met ‘vacuüm’ bedoeld wordt in natuurkunde. Misschien denk je bij het woord vacuüm aan een volkomen lege ruimte. In de quantummechanica is dat beeld echter onjuist: ook de meest ‘lege’ ruimte is nog altijd gevuld met allerlei velden. Bovendien is er geen toestand waarin alle velden zich in volledige rust bevinden en voor altijd in die toestand blijven: er is altijd een kans dat een veld ineens een trilling vertoont. In de quantummechanica bestaat er dus geen volkomen lege toestand, en met ‘vacuüm’ wordt daarom een toestand bedoeld die zo leeg mogelijk is. Opmerkelijk genoeg kan er meer dan één zo’n vacuümtoestand bestaan; het kunnen er zelfs oneindig veel zijn! De verschillende vacua in een natuurkundige theorie zijn aan elkaar gerelateerd door symmetrietransformaties. In het bijzonder veranderen de supertranslaties van Bondi, Metzner en Sachs de vacuümtoestand van het universum. Na zo’n vacuümtransitie keert het universum echter niet exact terug naar zijn oorspronkelijke toestand: er blijft een klein meetbaar verschil over – het geheugeneffect!
Heel veel infrarooddriehoeken
De infrarooddriehoek vertelt ons dus dat het verschuivingsgeheugeneffect, de zachtegravitonstelling en de BMS-symmetrieën wiskundig gezien exact hetzelfde zijn. Dit is een krachtig resultaat, omdat het helpt om de drie afzonderlijke onderwerpen beter te begrijpen. Aspecten die goed worden begrepen voor één van de drie hoeken, kunnen met behulp van de hierboven beschreven relaties vertaald worden naar aspecten van de andere twee hoeken, en helpen zo om ook die beter te begrijpen. (Zie ook dit artikel over dualiteiten – de infrarooddriehoek kan in deze taal een ‘trialiteit’ worden genoemd.)

Wat misschien nog wel veel spannender is, is dat er na de ontdekking van de eerste infrarooddriehoek een scala aan andere infrarooddriehoeken is ontdekt. Zo zijn er driehoeken die andere zachte stellingen bevatten (zoals de zachtefotonstelling of zachtegluonstelling), andere geheugeneffecten (zoals een verandering van de spin van elementaire deeltjes), en andere verzamelingen van symmetrieën (zoals de Virasoro-symmetrieën, die opduiken in de snaartheorie). In sommige gevallen is de driehoek compleet, maar er zijn ook driehoeken waarvan op dit moment slechts één of twee hoeken bekend zijn. Sinds de ontdekking van de PSZ-driehoek houdt een flinke groep natuurkundigen zich bezig met het verder uitbreiden van de verzameling van infrarooddriehoeken. De verwachte driehoeksstructuur maakt het mogelijk om gericht op zoek te gaan, waardoor ontdekkingen in dit gebied elkaar in rap tempo blijven opvolgen. De kans is dus groot dat je in de toekomst nog wel meer over dit onderwerp zal lezen op deze site.
QU is sinds kort weer actief op Instagram! Volg ons voor nieuws en aankondigingen van nieuwe artikelen: https://www.instagram.com/quantumuniverse.nl/