
De klassieke thermodynamica gaat over grootheden zoals entropie, temperatuur, energie, en druk. Deze grootheden waren al ver voor de ontdekking van de quantummechanica bekend. Nu we al meer dan 100 jaar de vreemde wereld van de quantummechanica kennen, is een natuurlijke vraag: kun je dezelfde thermodynamische grootheden toekennen aan een quantumsysteem? Stel dat zich binnen in een hete quantumcomputer bijvoorbeeld 10 qubits bevinden, kun je dan zeggen dat die qubits ‘opwarmen’? Het verrassende antwoord is dat veel van de gebruikelijke wetten van de thermodynamica blijven gelden, mits het quantumsysteem sterk verstrengeld is met zijn omgeving.
Entropie en verstrengeling
Van Ludwig Boltzmann hebben we al in de 19e eeuw geleerd dat de klassieke thermodynamica een geheel is van statistische wetmatigheden over willekeurig bewegende deeltjes, zoals moleculen in een gas. Een centrale grootheid in de zogenoemde statistische fysica is de entropie S, in een formule beschreven als
\( S = -k_B \sum_n p_n \log p_n \).
Hier is \( k_B \) de constante van Boltzmann, en \( p_n \) de kans dat het systeem in de n-de microscopische toestand is. De som van de kansen is gelijk aan 1. Als elke microscopische toestand (uit bijvoorbeeld W toestanden) even waarschijnlijk is, \( p_n = 1/W \), dan is
\( S = k_B \log W \).
Grofweg telt de entropie het aantal microscopische toestanden W met dezelfde macroscopische beschrijving. In het voorbeeld van een gas wordt een microscopische toestand beschreven door de positie en snelheid van alle gasmoleculen, terwijl de macroscopische toestand van het gas alleen afhangt van de temperatuur en de druk. In een gas dat in thermisch evenwicht is, zijn er erg veel manieren waarop de gasmoleculen kunnen rondbewegen op zo’n manier dat de gemiddelde temperatuur en druk hetzelfde blijven — het gas heeft dus een hoge entropie. Sterker nog: wanneer een systeem A in contact wordt gebracht met een ‘bad’ B (bijvoorbeeld een kop koffie die in contact staat met de lucht in de kamer), dan wordt thermisch evenwicht bereikt precies wanneer de entropie van het systeem A (en B) maximaal is.[1]
Hetzelfde principe geldt voor de quantum-statistische fysica. Daar wordt thermisch evenwicht ook gedefinieerd als de quantumtoestand met de hoogste entropie. In dit geval is de entropie echter niet een gewone entropie, maar de zogeheten Von Neumann-entropie of verstrengelingsentropie. Dit is een maat voor de hoeveelheid verstrengeling tussen twee quantumsystemen A en B. Net als in de vorige paragraaf nemen we aan dat systeem A het systeem is waarvan we de thermodynamische eigenschappen willen beschrijven, en B een ‘bad’ van veel quantumdeeltjes waarmee A verstrengeld is. De mate van verstrengeling wordt uitgedrukt door de verstrengelingsentropie:
\( S_{VN} = \, – \sum_n \lambda_n \log \lambda_n \).
In deze formule zijn \( \lambda_1 \) tot en met \( \lambda_N \) de eigenwaarden van de gereduceerde dichtheidsmatrix \( \rho_A \) die een toestand in systeem A beschrijft. Je hoeft om dit artikel te begrijpen niet precies te snappen wat een dichtheidsmatrix is of wat eigenwaarden zijn: het is voldoende om op te merken dat de formule hierboven voor de verstrengelingsentropie sterk lijkt op de eerste formule voor de klassieke entropie. De toestand met energie E waarvoor de verstrengelingsentropie maximaal is, noemen we de thermische toestand. De thermische toestand heeft een temperatuur die bepaald wordt door de energie E via een gebruikelijke thermodynamische relatie: \( 1/(k_B T) = S’(E) \) (de afgeleide van de entropie). Ook alle andere gebruikelijke thermodynamische wetten zijn van toepassing op deze thermische toestand. Kortom: we zien dat klassieke thermodynamische wetmatigheden ook gelden voor quantumtoestanden met maximale verstrengeling tussen systeem A en B.
Nu zou je kunnen denken dat een maximaal verstrengelde toestand een wel heel speciale toestand moet zijn, waardoor de vraag blijft: waarom vertonen algemene quantumtoestanden überhaupt thermisch gedrag? Er bestaat in de quantumfysica geen wet zoals in de klassieke thermodynamica die zegt dat entropie altijd groeit en die dus natuurlijkerwijs tot een maximaal entropische toestand zou leiden. Dit komt doordat de Von Neumann-entropie hetzelfde is voor een toestand \( \rho_A(0) \) op tijdstip t=0 als voor de toestand \( \rho_A(t) \) een tijdseenheid t later. Met andere woorden, de maximaal verstrengelde toestand is niet een ‘eindstadium’ waar quantumsystemen in de tijd naartoe groeien. Waarom is het dan toch zo dat quantumsystemen die in contact staan met een bad B in thermisch evenwicht komen? Het antwoord is: het had niet anders kunnen zijn. Een maximaal verstrengelde toestand is namelijk helemaal niet zo speciaal als we misschien dachten, het is zelfs de typische toestand. Preciezer gezegd: wanneer systeem A plus systeem B zich in een willekeurige toestand bevinden, is de kans overweldigend groot dat die toestand bijna maximaal verstrengeld is. De kans om in thermisch evenwicht te zijn is dus simpelweg zo groot doordat de meeste mogelijke quantumtoestanden in A bijna volledig verstrengeld zijn met B. Dit feit wil ik in de volgende sectie verklaren aan de hand van een puur meetkundige eigenschap van de ruimte van mogelijke quantumtoestanden.
Intermezzo: de ruimte van quantumtoestanden
Een handige manier om quantumtoestanden wiskundig te beschrijven is als punten op een boloppervlak. Deze ruimte van toestanden is niet de gewone ruimte waarin wij leven, maar een abstracte ruimte die de mogelijke toestanden van een quantumsysteem beschrijft. Voor een qubit heet dit boloppervlak de Blochsfeer[2] (zie afbeelding 2); je kunt daar hier meer over lezen.
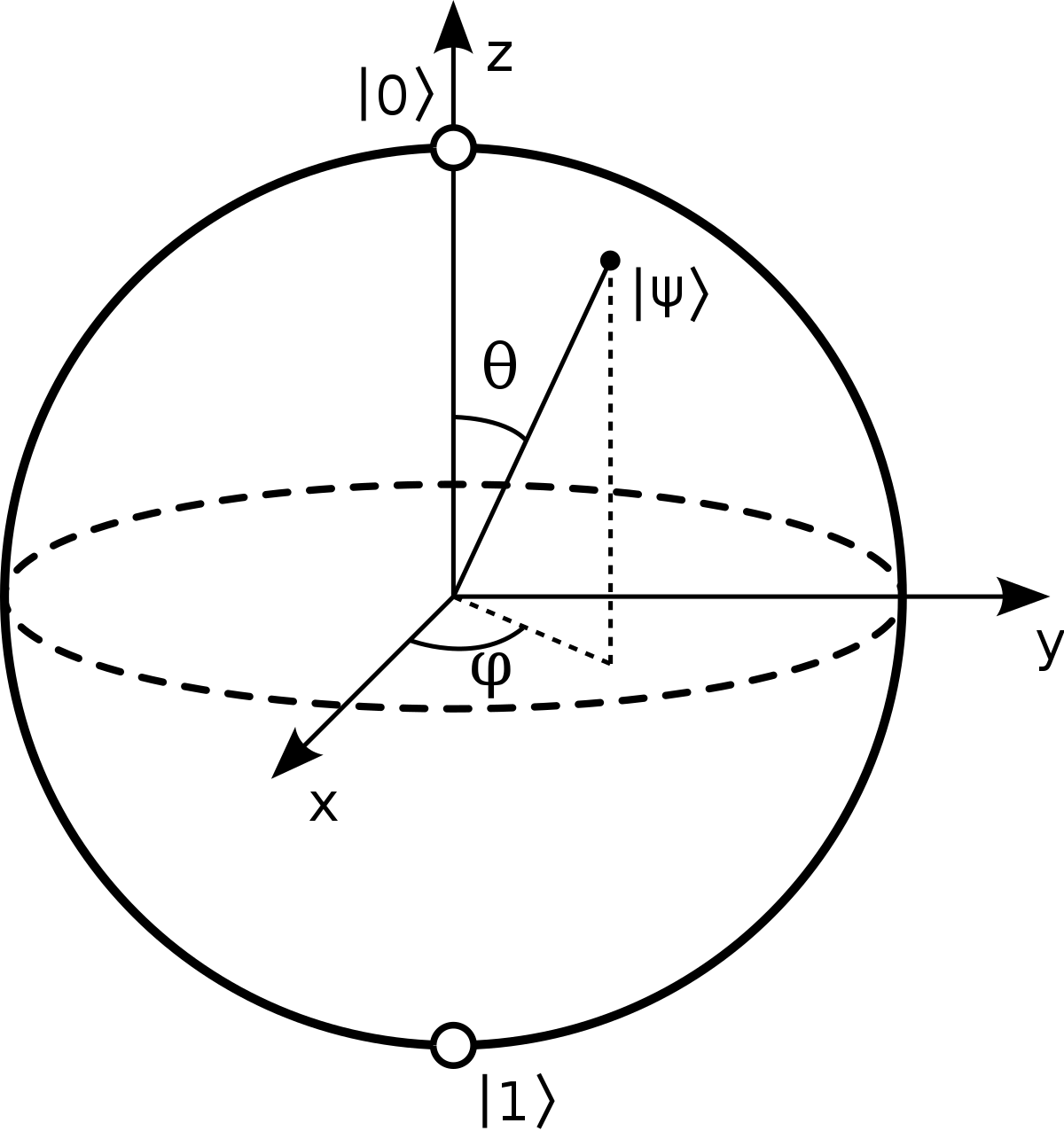
De systemen die ik hierboven beschreef bestaan niet uit een enkele qubit, maar uit veel meer quantumdeeltjes, dus de ruimte van mogelijke toestanden waarin het geheel zich kan bevinden is ook veel groter. De precieze definitie van ‘groter’ is dat de toestanden worden beschreven door het oppervlak van een hoog-dimensionale bol. Zo’n oppervlak wordt ook wel een ‘sfeer’ genoemd – maar wat is een hoger-dimensionale sfeer? Een 1-sfeer is een cirkel, die wordt beschreven door de vergelijking
\( x^2 + y^2 = 1 \).
Een 2-sfeer is het boloppervlak van een bol in drie dimensies, zoals een voetbal, en wordt beschreven door de vergelijking
\( x^2 + y^2 + z^2 = 1 \).
De 3-sfeer is het oppervlak van een vierdimensionale bol; die kunnen we ons al niet meer helemaal voorstellen. (Bijvoorbeeld: de ‘evenaar’ van de 3-sfeer is zelf weer een 2-sfeer). Ga zo verder naar de N-sfeer en het wordt steeds ingewikkelder om er een voorstelling van te maken. Wiskundig gezien is de N-sfeer echter een simpele veralgemenisering van de vergelijkingen hierboven:
\( x_0^2 + x_1^2 + … + x_N^2 =1 \).
Het blijkt dat een quantumsysteem dat bestaat uit systeem A (met dimensie \( D_A \)) plus systeem B (met dimensie \( D_B \)) wordt beschreven door een N-sfeer waarbij \( N = 2 D_A D_B – 1 \). Wanneer het systeem B (het ‘bad’) veel vrijheidsgraden heeft (\( D_B \) is dus groot) dan is de ruimte van toestanden dus het oppervlak van een zeer hoog-dimensionale bol!
Nu blijkt dat hoger-dimensionale bollen heel eigenaardige eigenschappen hebben, die sterk afwijken van onze dagelijkse intuïtie van bollen in drie dimensies. De eigenschap die voor dit artikel van belang is, is de volgende cryptisch klinkende uitspraak: bijna al het oppervlak van een hoog-dimensionale bol is geconcentreerd rond de evenaar. Dit fenomeen heet ‘concentratie van maat’, in het Engels concentration of measure. Voor onze welbekende 2-sfeer heb ik in een vorig artikel op deze website laten zien dat het oppervlak van een strook rond de evenaar even groot als is als dat van een strook in de buurt van de noord- of zuidpool, zolang de twee stroken maar dezelfde hoogte hebben.

In afbeelding 3 zien we dit afgebeeld: de rode strook links heeft hetzelfde oppervlak als de strook in het rechter plaatje. Zoals ik in het vorige artikel uitlegde is dit een gevolg van een balans tussen twee processen: wanneer je vanaf de evenaar naar de polen beweegt, wordt de omtrek van de bol kleiner, maar tegelijk wordt het oppervlak meer gekanteld. Deze twee effecten heffen elkaar op, waardoor het oppervlak van de strook gelijk blijft. Maar: dit is speciaal aan de 2-sfeer: voor een N-sfeer heffen deze processen elkaar niet op! De straal r van de dunne strook en de mate van kanteling blijven gelijk, maar de ‘omtrek’ neemt nu af als een hogere macht van de straal, namelijk \( r^{N-1} \). Voor een strook dicht bij de polen is r klein, waardoor \( r^{N-1} \) onevenredig veel kleiner is. Om een voorbeeld te geven: stel dat r = 0,1, en N = 100, dan is \( r^{N-1} \) gelijk aan 0,00…0001, met 99 decimalen na de komma — extreem klein, dus. Oftewel: een strook dichtbij de polen heeft een véél kleiner oppervlak dan een strook dichtbij de evenaar, doordat de verhouding van omtrekken schaalt met een hogere macht van de straal.
Waarom quantumsystemen in thermisch evenwicht zijn
Voor ons betekent de bijzondere eigenschap van bollen het volgende. Als je een willekeurige quantumtoestand kiest voor systeem A+B, dus een punt op het oppervlak van de N-sfeer, dan is de kans heel groot dat dit punt dicht in de buurt van de evenaar ligt, simpelweg omdat daar het ‘meeste’ oppervlak is. Het blijkt dat juist de quantumtoestanden die ‘in de buurt van de evenaar’ liggen allemaal bijna maximaal verstrengeld zijn. Oftewel: als N maar groot genoeg is (dus in het bijzonder: als het bad B bestaat uit veel deeltjes), dan is met overweldigende waarschijnlijkheid bijna elke willekeurige quantumtoestand ongeveer maximaal verstrengeld. Anders gezegd: de deelruimte van quantumtoestanden die bijna maximaal verstrengeld zijn, bestrijkt vrijwel de gehele ruimte van mogelijke quantumtoestanden. Dit verklaart waarom systemen die in contact staan met een bad B met veel deeltjes thermisch gedrag vertonen!
Voor wie geïnteresseerd is eindig ik dit artikel door de bovenstaande beweringen wiskundig wat preciezer te maken. Het fenomeen van concentratie van maat op de N-sfeer wordt uitgedrukt door de volgende stelling. Neem een functie die een punt x op het boloppervlak stuurt naar de functiewaarde f(x), en stel dat deze functie niet al te snel varieert. Noem het gemiddelde van de functie over de bol E[f]. Dan is voor een willekeurige x de kans dat het verschil tussen f(x) en zijn gemiddelde, E[f], groter is dan \( \epsilon \) altijd strikt kleiner dan
\( e^{-C N \epsilon^2} \).
Hierin is C een constante waarvan de precieze waarde niet van belang is. Wat er wel toe doet is dat, wanneer je \( \epsilon \) groter maakt (dus hoeveel de functiewaarde verschilt van zijn gemiddelde), de kans om de bijbehorende functiewaarden te vinden exponentieel afneemt. En hoe groter N is, hoe sterker de exponentiële afname wordt. Simpel gezegd is de functie f(x) met grote zekerheid ongeveer constant wanneer N maar groot genoeg is. Toegepast op ons onderwerp van quantumverstrengeling kunnen we voor de functie f daarom de verstrengelingsentropie nemen: de vergelijking
\( S_{VN} = \, – \sum_n \lambda_n \log \lambda_n \).
die we eerder zagen is namelijk precies een functie die aan een punt op een bol (een quantumtoestand) een functiewaarde toekent (de entropie). De gemiddelde entropie, E[f] in onze notatie van zojuist, ligt vlak bij de maximale verstrengeling.[3] Passen we de bovenstaande stelling toe, dan zien we dat de kans dat een willekeurige quantumtoestand x een verstrengelingsentropie heeft die sterk afwijkt van het gemiddelde, dus exponentieel klein is. Dit maakt de bewering precies dat een willekeurige quantumtoestand van een systeem dat in contact staat met een bad met grote waarschijnlijkheid bijna maximaal verstrengeld is, en dus de thermische eigenschappen heeft die we uit ons dagelijks leven kennen. Iemand toevallig zin in een kopje quantumkoffie?
Bronnen
- Patrick Hayden, Entanglement in random subspaces, https://arxiv.org/pdf/quant-ph/0409157.pdf
- Popescu et al, The foundations of statistical mechanics from entanglement, https://arxiv.org/pdf/quant-ph/0511225.pdf
- Goldstein et al, Canonical typicality, https://arxiv.org/pdf/cond-mat/0511091.pdf.
[1]Een technische aanname hier is dat de totale energie van systeem plus bad constant blijft.
[2] Overigens wordt de Blochsfeer ook vaak de Blochbol genoemd. Onthoud bij die laatste naam wel dat het alleen gaat om het oppervlak van de bol!
[3] De maximale verstrengelingsentropie is de logaritme van N. De gemiddelde verstrengelingsentropie voor een uniforme kansverdeling op de sfeer is log(N) – 1/2. Maar voor grote N is de –1/2 verwaarloosbaar klein.