Graph theory is a relatively modern branch of mathematics with many fascinating applications. The main objects of study in this field are graphs, i.e., structures that consist of points (also called vertices or nodes) that are connected by lines called edges or links. An important feature of graphs is that they do not really care about the exact geometric positions or distances between the nodes. Instead, they focus on relationships and connectivity. In this sense, graphs are abstract representations of how things are connected, not where exactly they are. Because of this, graph theory is closely related to ideas that are central in modern mathematics and physics, such as topology and knot theory.
This makes graph theory extremely useful in areas like computer science and data science. For example, it is often used to study social networks. A well-known case is the analysis of platforms like Twitter (now called “X”). In a study by Grandjean (2016), the network structure was modelled using graph theory: users were represented as nodes, and a link was added between two users if they followed each other. Users who were not connected had no edge between them. In this way, the researchers could represent “who-follows-who” relationships and apply mathematical reasoning to visualize large amounts of data, identify clusters of sub-communities, and find especially influential users.
Another striking example for the power of graph theory comes from physics: Feynman diagrams in quantum field theory. These are graphical representations of extremely complicated mathematical calculations that describe how elementary particles interact and decay. Even though they look like simple drawings, each element in a Feynman graph has a precise mathematical meaning. Thus, a single diagram – that is: a single graph – can summarize a long and complex computation in a visual and intuitive way.
While these modern applications are fascinating, in this article we will go back in time to learn about what is often called the first theorem in graph theory. This first theorem is known as the Königsberg bridge problem and was solved (or more precisely, shown to be unsolvable) by the famous mathematician Leonhard Euler in 1736. You can even read Euler’s original proof, written in Latin, in his paper Solutio problematis ad geometriam situs pertinensis. Or click on this link for an English translation, “Solution of a problem in the geometry of position”.
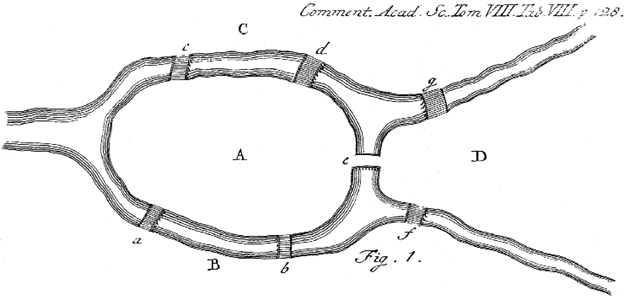
During Euler’s time, the Prussian city of Königsberg (today called Kaliningrad, in Russia) was built on both sides of the river Pregel and included two islands, called Lomse and Kneiphof. These islands were connected to the mainland areas on each side of the river, Altstadt and Vorstadt, and to each other by seven bridges (see figure 1).
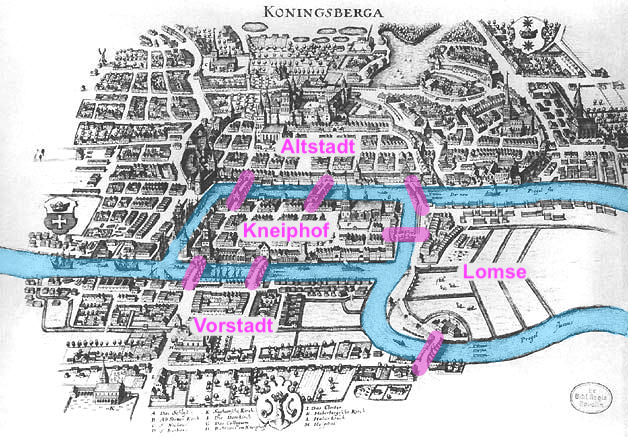
The statement of the problem was rather simple: Can you find a walk through the city that reaches each landmass while crossing each of the seven bridges exactly once? To clarify the rules: you may only move between land areas using bridges – swimming and long jumping are forbidden! Moreover, once you have stepped onto a bridge, you must cross it completely. You are not allowed to turn around halfway and backtrack on your path.
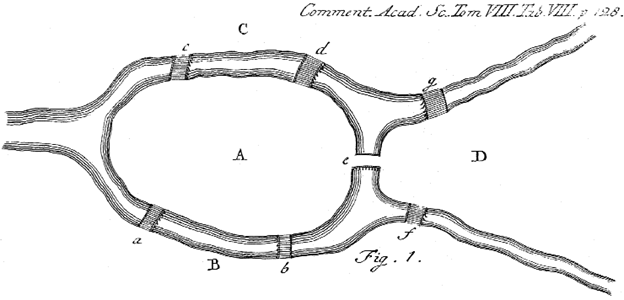
Many people tried to solve this as a puzzle. But Euler took a completely new and revolutionary approach by abstracting the problem. In fact, he realised that a complicated real-world problem could be simplified by focusing only on the essential elements. In the case of the seven-bridge problem, the exact paths you take within each land area do not actually matter. To assess whether a path of the desired sort exists, the only truly important thing is the order in which you cross the bridges. Thus, Euler realised that he could reduce (or abstract) the entire city layout to four land masses (labelled A, B, C, D in figure 2) and seven bridges connecting them (labelled a, b, c, d, e, f, g in figure 2).
In a further step of abstraction, he represented each land mass as a node (vertex) and each bridge as an edge (link) between nodes. In this way, he translated the layout of the city of Königsberg into an abstract graph. (See figure 3.)
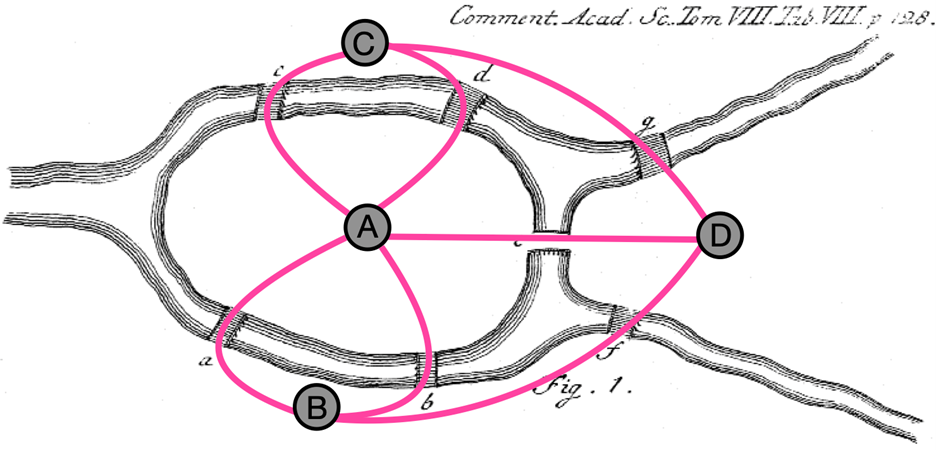
This graph-representation turned the original walking problem into a new question: Can you draw all the edges of this graph in one continuous stroke, without lifting your pen and without re-tracing any edge once you have drawn it? If this is possible, the graph is said to have an Eulerian path. Euler also realized that the exact shape of the graph does not matter, only the connectivity does. You can move the nodes around or bend the edges, as long as you do not cut or glue any connections. These ideas are early precursors of topology, the modern branch of mathematics where shapes are considered equivalent if they can be smoothly deformed into each other. (The famous example is that a coffee mug and a doughnut are topologically the same because they both have one hole and can therefore be deformed into one another.)
Upon studying the problem in its graph representation, Euler then made a crucial observation: In any walk through the graph, whenever you enter a node you must also leave it again (except possibly at the start or end). That means that, for most nodes, edges come in pairs: one to enter and another one to leave. From this Euler concluded that, in order for a graph to have an Eulerian path, most nodes must have an even number of edges touching them. The number of edges connected to a node is also called its degree. In fact, to find an Eulerian path, at most two nodes in any graph are allowed to have an odd degree: one for the start of the path and one for its end. And if the path is a closed loop that starts and ends at the same node, also known as Eulerian cycle, then none of the nodes may have odd degree.
Looking at the Königsberg graph in figure 3, you can see that all four land masses are connected to an odd number of bridges. One has five bridges, and the other three each have three bridges. That means there are four nodes with odd degree, which makes an Eulerian path or cycle impossible. In this way, Euler proved that the seven-bridge problem has no solution. No matter how cleverly you try, you cannot reach every land mass by crossing all seven bridges exactly once.
Euler in fact did a bit more: he also showed that once the condition on the number of edges is satisfied, a walk through the graph with the given conditions does exist. In modern mathematical language, Euler showed that a connected graph has an Eulerian path if and only if it has exactly zero or two nodes of odd degree. Since the Königsberg graph has four nodes of odd degree, the problem as it was stated (“Find a path such that…”) is unsolvable.
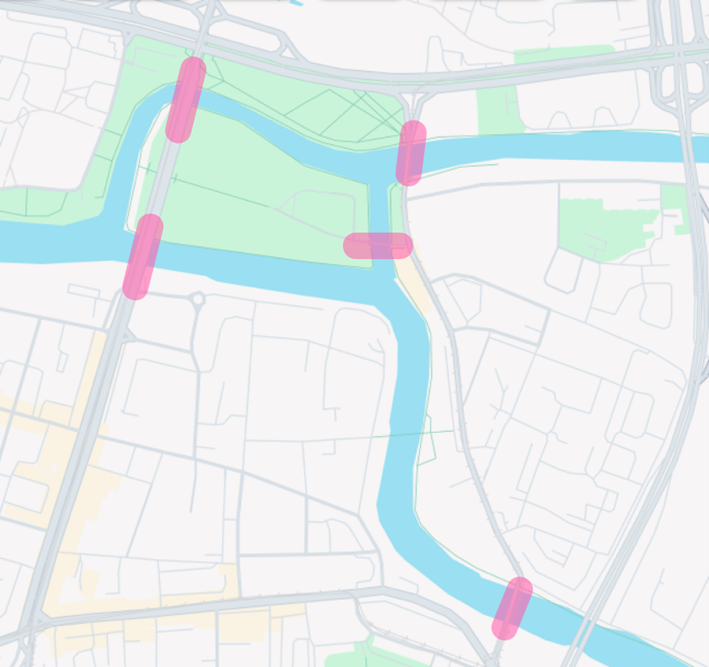
As a fun fact, the layout of the bridges in Königsberg (nowadays Kaliningrad) has changed over time. Today, only five bridges remain (see figure 4) to connect the four land masses. This means that the modern version of the problem is different from the one Euler studied. As a challenge, can you translate the modern city map into a graph with nodes and edges, just like Euler did? Can you then work out whether the modern “Kaliningrad bridge problem” is solvable or not? I may tell you the answer in a follow-up article!
References
Grandjean, Martin. “A social network analysis of Twitter: Mapping the digital humanities community” Cogent arts & humanities1 (2016): 1171458.
Euler, Leonhard. “Solution of a problem in the geometry of position”. Commentarii Academiae Scientarum Imperialis Petropolitanae 8 (1736)