
Figure 1. Don’t Panic?During the COVID-19 crisis there have been multiple countries with a toilet paper shortage. Using game theory, we can get some insights into this phenomenon. Image: Jasmin Sessler.
Imagine you just heard the news that there is going to be a national lockdown due to the coronavirus pandemic. You don’t know for how long this will last, but you do know that you will still need access to supplies, such as food, cleaning products… and toilet paper! You could run to the supermarket and try to hoard as much as possible, in which case other people might not be able to get anything from the supermarket after you. Or you could just do your groceries as usual and assume you will be able to come back and do your next grocery run. In choosing this option however, you might be left with nothing when other people do decide to hoard. What would you do?
Game theory
It turns out that this “toilet paper dilemma” can be studied using what’s known as game theory. Broadly speaking, this is the science of strategic and logical decision-making among individuals. The dilemma described above can be expressed as a mathematical model – a ‘game’ – in which you and the rest of the people are the players [1].
Much of the groundwork of game theory was laid down, starting in 1928, by John von Neumann: mathematician, physicist, computer scientist, and engineer. Another important figure in the development of the field was the mathematician John Nash, who has been described as “one of the most original minds of the twentieth century” [2] and even got his own biographical movie while still alive: A Beautiful Mind. Nowadays, game theory is used in a broad range of both natural and social sciences, being especially important in economics, logic and computer science. However, the applications don’t end there! While we won’t delve into this now, there is even such a thing as quantum game theory which makes a direct link to quantum physics. Here, we will use game theory to understand why, in times of lockdown, you see people with more toilet paper packs than their bicycles can carry, even though collectively everyone would be better off by just buying the usual amount.

Figure 2. A beautiful mind.John Nash, one of the most notable contributors to game theory, got his own biographical film in 2001.
The rules of the game
To model the scenario we need the following assumptions:
- The players in the game are “you” and “everyone else”. Or ‘players 1 and 2,’ for convenience.
- The game starts when the lockdown is announced. All players receive the announcement at the same time.
- Players want to have access to toilet paper (TP) for as long as possible. We define access by either having it at home or being able to buy it from the supermarket, and we assume that players do not start with a stash of TP at home.
- The key assumption is that the supermarket only has stock for people buying the usual amount. Therefore, if someone buys more than usual the others won’t have enough access.
- Once the game starts, the players must make a choice between two options:
(1) Go and buy as much TP as possible and hoard it at home (we will call this action H for Hoarding),
(2) Just buy the usual amount, assuming they will be able to go back to the supermarket at some point to get more (we will call this action N for ‘Not hoarding’).
The players have no means of communication once the lockdown is announced. This means neither of the players knows what decision the other one is going to take before deciding what to do themselves.

Figure 3. To hoard or not to hoard, that is the question.Image: PXFuel.
Players’ preferences determine the outcome
Now we know the rules of the game, but what types of players do we have? Different kinds of players may assign different values to the possible outcomes of the game, depending on their personal preferences (natural hoarders do exist!), and what they expect the other player to do. This is where mathematics enters the game: by knowing how players value all possible outcomes, we will be able to figure out the logical outcome.
To understand how this works, let’s try playing the game with two players who are selfish, in the sense that they prioritise their own access to TP over the well-being of the other player. Motivated by the fear of others hoarding, leaving them with no access to TP, and wanting to ensure their own TP stash is doomsday-proof, these players will rationally conclude that it is best for them to hoard.
Their reasoning can be explained as follows. If you know other people are not hoarding, good for you! You get all the TP you want. If you know everyone else will hoard, you should also run and hoard to get as much as possible. This means that regardless of what the other player decides to do, both players prefer to hoard. We can represent this mathematically by using so-called action profiles. Action profiles are a way of representing the actions of both players. An action profile is written as (1, 2), with the actions of player 1 and player 2 filled in. For example, the action profile (H, N) means that player 1 intends to Hoard, while player 2 intends to Not hoard.
In the example above, we can express the preferences of player 1 (you) by writing which action profiles you prefer as
(H,N) > (N,N) and (H,H) > (N,H)
Because this is a symmetric game in which both players have the same order of preference, player 2 will have the exact same reasoning.
Finally, we will assume our players are ‘moderate hoarders’, meaning that they prefer both players buying the usual amount of TP over both of them hoarding. Being instinctively conflict-avoiding, they prefer not to fight over the finite amount of TP. In other words, they prefer to share:
(N,N) > (H,H)
This gives us the complete ordering for player 1’s preferences:
(H,N) > (N,N) > (H,H) > (N,H)
From a game to a matrix
Thinking about the complete preference order of possible outcomes, you can argue that these players will prefer to hoard, as we did in words above. Game theoreticians have a more insightful way of representing these preferences, in what’s called a payoff matrix. Given the preference order, we can write down a table where the rows correspond to the two possible actions of player 1 and the columns to those of player 2. The numbers in each box are the players’ payoffs (i.e. how much they benefit) from the actions taken by both players, with the outcome for player 1 listed first. It isn’t important which specific values we assign to the payoffs, as long as the preference order is correct. For our current game, we would for example obtain table 1, shown below.
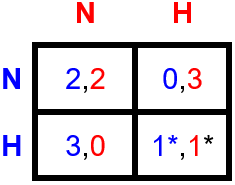
Table 1. Two moderate hoarders.Preference matrix for the toilet paper dilemma between two moderate hoarders. Rows correspond to the decisions of player 1 (blue), columns to those of player 2 (red). The first entry of each cell corresponds to the results for player 1, and so on. Denoted with a * is the best response for each player in equilibrium. (This convention will be used in the following examples.)
How much players benefit from each possible set of choices made by the two players can now be directly read off from the table. If for example you choose H and the others choose N we have to look at the bottom-left cell in which you have a payoff of 3 and the others have a payoff of 0. When both players try to maximize their own outcome, they end up in the bottom-right cell, each hoarding, each with an outcome of 1.
Nash equilibrium
At this point, you might wonder how two rationally thinking players would prefer to end up with a payoff of 1 (from the outcome (H,H)), while they would both benefit more if neither would hoard, because (N,N)>(H,H). Sadly, given that they both prefer to be the only ones hoarding, they always have an incentive to choose H, and even if the other one chooses H they will still have a better payoff than in the case in which they chose N (for example, (N,H) is worse than (H,H) for player 1). This incentive eliminates the possibility that the mutually desirable outcome (N,N) occurs. Cooperating or choosing N is, from a self-interested perspective, irrational.
In this example, (H,H) is what is called a Nash equilibrium, named after John Nash mentioned earlier. In a Nash equilibrium no player can do better by changing their own action unilaterally. This means that the final outcome is the action profile for which every player’s action is a best response to the other players’ actions. More than just a mathematical curiosity, such a Nash equilibrium embodies a stable “social norm”, namely: if everyone else is hoarding, why shouldn’t you try to hoard? With this reasoning, no single person wishes to change the norm even if in the end it is not the most beneficial outcome for anyone [3].
Then again, here we have assumed that our players don’t value the well-being of their neighbours. We also assumed that everyone has the same order of preferences. Considering other types of players, our game might give us a different, and perhaps more positive outlook on society.
Not all hoarders are the same
We could for example think of extreme hoarders, who are players with preferences based on the idea that the best thing to do is always to hoard as much as possible, even if that means fighting over it. Of course, they also still prefer having access from the supermarket over not having access at all. The payoff matrix for two extreme hoarders playing against each other is presented in table 2. There is no dilemma here: the Nash equilibrium corresponds to (H,H) and in this case the players even prefer this over (N,N). So it is straightforward to see that under this mindset, the best option is to always choose H.
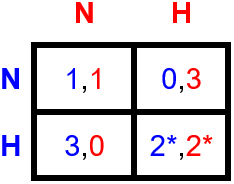
Table 2. Two extreme hoarders.Payoff matrix for two extreme hoarders with preference (H,N) > (H,H) > (N,N) > (N,H).
Compare this to players who prefer not having their houses overflowing with supplies while still having access from the supermarket. We will call such players non-hoarders. They do still prefer having the supplies in their houses over having no access to them at all. And they prefer being the only ones hoarding over both hoarding, since then their access to supplies would be shorter. With these preferences we obtain the following payoff matrix for two non-hoarders:
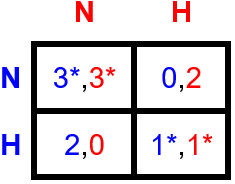
Table 3. Two non-hoarders.Payoff matrix for two non-hoarders with preference (N,N) > (H,N) > (H,H) > (N,H).
From this we can tell that there are two Nash equilibria, namely (N,N) and (H,H). In both of these cases, changing your own decision while the other player does not change leads to a worse outcome, so neither player will want to change. This example is useful to see that a Nash equilibrium doesn’t necessarily mean that the action a player takes is a best response against every possible action of the other player. For example in this case N is the best response if you expect the other player to play N, and similarly H is the best response if you expect the other player to go for H. This is different from the moderate hoarder’s dilemma that we considered before, where H was the best response to any action taken by the other player.
The theory of Nash equilibria does not predict which equilibrium out of the two will emerge as a steady-state any time you play. There might be other features not modeled in the game that steer the decisions made by the players by drawing their attention to one specific equilibrium.
This would explain why even if the two players are non-hoarders, the emerging outcome could be (H,H) regardless of (N,N) being the perfect outcome for both of them. The players might be influenced by their knowledge of the two previous games studied (moderate and extreme hoarder cases). Because (H,H) is the only Nash equilibrium in those two games, it may attract the attention of the non-hoarder players, or perhaps they read in the news about how other countries ran out of supplies and assume that the same will happen to them. In such cases (H,H) may be the natural outcome even if everyone is a non-hoarder. However, regardless of (H,H) becoming a focal point, (N,N) remains a better outcome for everyone! So if you know that you are playing against another non-hoarder and therefore believe they have indeed reasons to choose N, the best option would be to cooperate.
Non-symmetric games
Until now we have been dealing with games in which both players have the same preferences, but what happens if you have a non-hoarder playing with a hoarder? Everything in the structure of the games is the same except for the payoff functions, so it is easy to combine the different preferences in a new payoff matrix.
The case of a non-hoarder playing with an extreme hoarder results in the following payoff matrix:
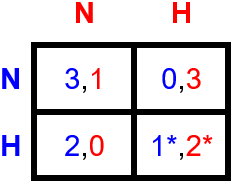
Table 4. An asymmetric game.Player 1 (blue) is a non-hoarder, player 2 (red) an extreme hoarder.
From this we can see that from the two Nash equilibria available to a pair of non-hoarders there is only one left, corresponding to (H,H). This also gives us an explanation to why non-hoarders might choose it as a focal point when playing, since they might not trust the identity of the other player and fear they are playing against an extreme hoarder.
Another interesting thing to notice is that an equilibrium does not necessarily give the same payoff to both players. Player 2 will be better off when in equilibrium than Player 1, but neither can improve upon their current situation by single-handedly changing their action.
Hoarders on a spectrum
As we previously saw we can incorporate different types of players by changing their preferences. Actually these preferences can be modeled by mathematical functions representing their altruism (how much they care about the wellbeing of others) as well as some kind of intrinsic hoarding behaviour, which could be motivated by fear of repeatedly going to the supermarket or by how frowned upon hoarding is by society.
For example, if we want to tune from a moderate hoarder to a non-hoarder, we would increase the parameter corresponding to how much incentive there is to not hoard. If we want to reach the extreme hoarding case we only need to decrease their altruism, which shows us that behaving like an extreme hoarder is effectively equivalent to preferring a bad outcome for your neighbours.
Repeated games and conclusion
In most of the studied cases, we have seen why hoarding tends to be the only logical outcome even though people might benefit from cooperation in the majority of circumstances. There still is hope for optimists, however. In practice, it turns out we have had the possibility to go to the supermarket more than once since the corona-virus outbreak was announced, at least in the Netherlands, and therefore we are constantly repeating the game. More importantly, we can constantly check if everyone else is hoarding or not.

Figure 4. Cooperation.Cooperation can result in a better outcome for everyone by increasing the ‘punishment’ assigned to hoarding. This could mean how frowned upon hoarding is by society or how much the others will retaliate when playing repeatedly.
It was proven in a computer tournament that when you play a game of this type iteratively, the winning strategy is actually to be nice until other players start to misbehave [4]. This strategy is known as tit-for-tat. Basically, you choose to cooperate or not hoard until the other one decides to hoard, after which you continue hoarding unless the other one decides to cooperate again. Therefore, if everyone decides not to hoard in the first round, you could keep going like that without ever having to compete with your neighbours! And if they do hoard at first but stop hoarding, tit-for-tat is a forgiving strategy. You may want to consider that game theoretic option next time you’re in a supermarket deciding how many rolls of toilet paper to buy.
Notes
[1] This game is usually known as the prisoner’s dilemma and it is presented by a different story which involves two convicts deciding whether to betray their partner to receive a shorter sentence. Hopefully, you are more familiar with the hoarding situation than with the convicts scenario.
[2] Kuhn, H. “Introduction”, Duke Mathematical Journal 81, i-v, 1996.
[3] Osborne, M. An Introduction to Game Theory. Oxford University Press, New York, 2009.
[4] Axelrod, R. The Evolution of Cooperation. Basic Books, New York, 1984.