Waar komt massa vandaan? IJktheorieën

Laat ik eerst de belangrijkste lessen van het eerste artikel in dit tweeluik dat geen tweeluik zal blijven kort herhalen. In dat artikel hebben we geleerd dat symmetrieën zoals rotatiesymmetrie of een symmetrie onder verplaatsing heel krachtig zijn in de natuurkunde. Ze impliceren namelijk dat er een behouden grootheid is: ruimtelijke verplaatsingssymmetrie impliceert behoud van impuls; symmetrie onder verplaatsing in de tijd impliceert behoud van energie, en rotatiesymmetrie impliceert behoud van impulsmoment. Dit volgt uit de zogenaamde stelling van Noether.

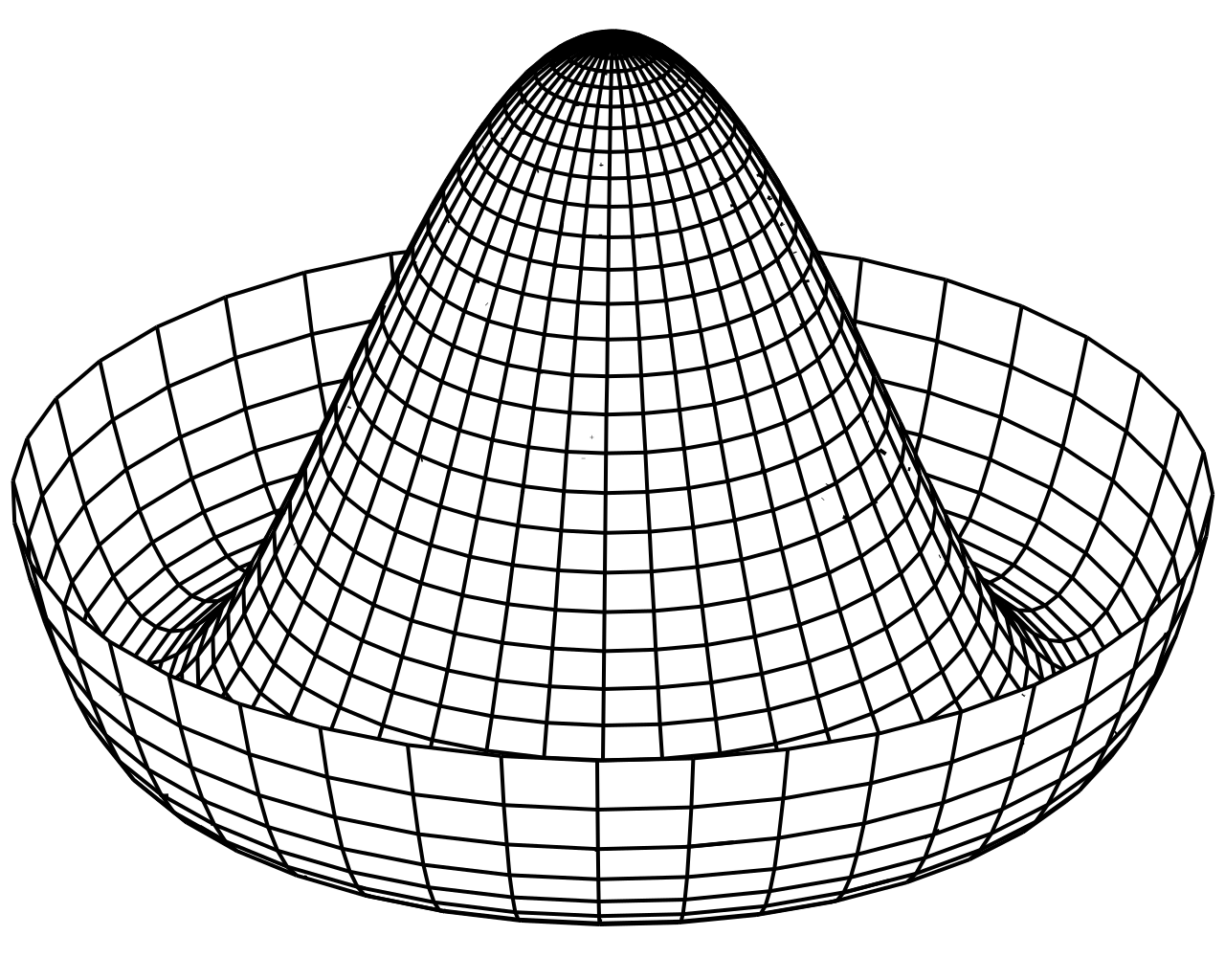
Het komt echter vaak voor dat de meest symmetrische toestand van een systeem niet de toestand met de laagste energie is. Wat er dan kan gebeuren is dat er spontane symmetriebreking plaatsvindt: het systeem valt spontaan naar een lagere energietoestand, die minder symmetrie heeft dan de initiële toestand. Een belangrijk gevolg hiervan is het zogenaamde Nambu-Goldstone-effect. Dat stelt dat als een continue symmetrie breekt  –  zoals bijvoorbeeld de rotatiesymmetrie van een cirkel – er een of meer massaloze deeltjes ontstaan, die we Nambu-Goldstonebosonen noemen. Die Nambu-Goldstonebosonen zijn geen fundamentele deeltjes maar zogeheten quasi-deeltjes. We hebben in het eerste artikel gezien hoe dit werkt voor een simpel geval met een potentiaal in de vorm van een Mexicaanse hoed – zie afbeelding 2.

Om een fysisch voorbeeld te geven: wanneer een vloeistof bevriest breekt de continue verplaatsingssymmetrie tot de discrete symmetrie van een kristalrooster. Er ontstaan dan ook Nambu-Goldstone bosonen, die we in dit geval fononen noemen. Deze fononen beschrijven de voortplanting van geluid door de vaste stof!

IJksymmetrie

Tot zover de lessen uit het vorige artikel – sla het er vooral nog even op na voor de precieze details. Wat we graag willen doen, is het bovenstaande verhaal toepassen op zogenaamde ijksymmetrieën, wat, zoals ik in het vorige artikel al vertelde, helemaal geen symmetrieën zijn. Deze transformaties worden daarom ook wel vaak ijkvrijheden genoemd. Ze beschrijven een bepaalde overbodigheid in de theorie die je gebruikt om een bepaald fenomeen te beschrijven. Je hebt dan de vrijheid om iets in je beschrijving aan te passen, zonder dat de fysische situatie daarmee verandert. Dit staat in sterk contrast met de eerdergenoemde echte symmetrieën, waar je wel degelijk fysisch iets verandert, maar bepaalde aspecten van je systeem onder die verandering invariant zijn. Bij een ijksymmetrie verander je niets wezenlijks, je verandert alleen de wiskundige beschrijving van de situatie.

Hoewel ijksymmetrie een van de meest subtiele concepten uit de natuurkunde is, ben je iets vergelijkbaars in je natuurkundeles op de middelbare school zo goed als zeker tegengekomen, ook al wist je dat waarschijnlijk niet. Iedereen weet bijvoorbeeld dat hoogspanningsmasten levensgevaarlijk kunnen zijn: als je vanaf de grond contact maakt met de kabels, zal er een enorme stroom door je lichaam lopen vanwege het spanningsverschil. Hoe komt het dan dat er vaak allerlei vogels gewoon vrolijk op die spanningslijnen zitten en hen niets overkomt, zoals in afbeelding 1? Hebben ze rubberen pootjes? Het antwoord is dat de stroom alleen gaat lopen ten gevolge van een spanningsverschil. Als de spanning op de grond 0 volt is, en de spanning op de draad zo’n 100 kilovolt, dan gaat er dus een grote hoeveelheid stroom lopen als je de twee verbindt met een voorwerp dat makkelijk elektriciteit geleidt, oftewel: een lage weerstand heeft. Dit is simpelweg de wet van Ohm. Het spanningsverschil tussen het ene pootje van de vogel dat de spanningslijn aanraakt en het andere pootje is 0 volt, aangezien beide dezelfde spanningslijn aanraken. De rest van het lichaam van de vogel is in contact met de lucht, die geen stroom geleidt. Er is dus ook geen reden dat er stroom zou gaan lopen door het lichaam van de vogel. Het enige wat ertoe doet is het verschil in spanning: ik kan ook kiezen om het nulpunt van spanning op te schuiven. Ik tel simpelweg een miljoen volt op bij zowel de spanning van de grond als de spanning van de hoogspanningslijn, maar het verschil, en dus elke fysische gebeurtenis, is onafhankelijk van mijn keuze. We zeggen dat we een ander ijkpunt voor de spanning hebben gekozen – vandaar ook de naam “ijkvrijheid” voor dit soort verschijnselen.

Een vergelijkbare situatie ben je misschien tegengekomen als je ooit de potentiële energie van een kleine massa in het zwaartekrachtsveld van de aarde hebt moeten opschrijven:

\( E_{pot} = mgh~, \)

waar \( m \) die massa is, \( g \approx 9{,}8 m s^{-2} \) de valversnelling op aarde en \( h \) de hoogte van die massa ten opzichte van een bepaald nulpunt. Ook hier maakt het niet uit waar ik dat nulpunt kies: de kracht die op de massa uitgeoefend zal worden, is alleen afhankelijk van verschillen in deze potentiële energie op verschillende hoogtes.

Elektromagnetisme

Het simpelste voorbeeld van een ijktheorie – een theorie met ijksymmetrie – is elektromagnetisme. Vorige week is daar op deze site al een artikel over verschenen van redacteur Sarah Jansen: over de Maxwellvergelijkingen. Waar in dat artikel al op gewezen wordt, is dat elektriciteit en magnetisme eigenlijk twee zijden van dezelfde munt zijn: een verandering in het magnetische veld in de loop van de tijd veroorzaakt een rotatie in het elektrische veld (de wet van Faraday), en de rotatie van het magnetische veld is weer afhankelijk van de verandering van het elektrische veld in de loop van tijd, en van een elektrische stroomdichtheid (de wet van Ampère en Maxwell).

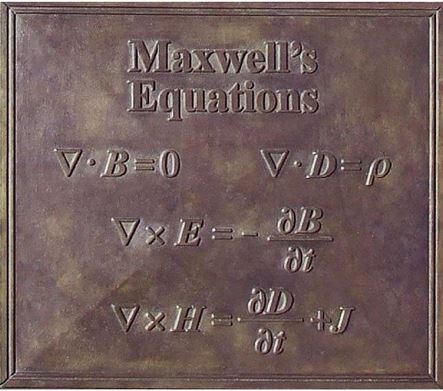
Als je alle verbanden tussen elektriciteit en magnetisme die uit de Maxwellvergelijking volgen meeneemt, blijkt dat je zowel het elektrische als het magnetische veld kan schrijven in termen van dezelfde viervector-potentiaal. Ook dit is een vectorveld – een uitstekende uitleg daarvan kan je terugvinden in het artikel van Sarah. In het kort: een veld is iets wat op elke plek in de ruimte en elk moment in de tijd een waarde heeft – denk aan bijvoorbeeld een temperatuurveld, dat aangeeft wat overal en op elk moment de temperatuur is. Met andere woorden: een veld is een functie die afhangt van ruimte- en tijdcoördinaten. Een vectorveld heeft daarnaast ook op elke plek en tijd een bepaalde richting: denk aan een stromingsdiagram dat luchtstromen in een ruimte aangeeft op verschillende tijden.

Je kan de viervector-potentiaal voor het elektromagnetisme opschrijven als een lijst van vier functies – één tijdcomponent en drie ruimtelijke componenten – die samen aangeven dat het vectorveld op die tijd en plaats in de betreffende richting wijst. De tijdscomponent, die we \( \phi \) noemen, heet de elektrische potentiaal, en de ruimtelijke componenten noemen we samen \( \textbf{A} \): de magnetische potentiaal. De dikgedrukte letter geeft aan dat het veld drie ruimtelijke componenten bevat.

De belangrijkste les uit het bovenstaande is dat je nu de elektrische en magnetische velden kan afleiden uit de viervector-potentiaal. Het magnetische veld wordt simpelweg gegeven door de rotatie van de magnetische potentiaal (zie wederom het artikel van Sarah):

\( \textbf{B} = \nabla \times \textbf{A}~ \)

waar je \( \nabla \times \) kan lezen als ‘rotatie van’ – denk aan de lijnen in een stroomdiagram die roteren, zoals water dat rondom een putje cirkelt voordat het wegloopt. Het elektrische veld wordt daarentegen gegeven door

\( \textbf{E} = -\nabla \phi – \frac{1}{c}\frac{\partial \textbf{A}}{\partial t}~, \)

waar \( c \) de lichtsnelheid is, en \( \nabla \phi \) de gradiënt van \( \phi \) aangeeft: een nieuwe vector met als componenten de ruimtelijke afgeleiden van \( \phi \). Dat wil zeggen: de richtingen van het hiermee ontstane vectorveld geven aan in welke richting \( \phi \) het meest verandert.

De wiskundige beschrijving hierboven is vrij technisch, en als het niet allemaal helemaal duidelijk is, is dat niet erg: de rest van dit artikel is ook te volgen zonder de wiskunde helemaal te begrijpen. Het belangrijke is zoals gezegd dat de elektrische en magnetische velden allebei uit de genoemde potentialen afgeleid kunnen worden. Er is daarbij echter een bepaalde vrijheid: we kunnen de potentialen ook anders kiezen, zonder de resulterende elektrische en magnetische velden te veranderen. Er is dus een ijksymmetrie!

Voor wie ook hier de wiskundige details wil weten: de transformaties die de definitie van de elektromagnetische velden ongedeerd laten zijn

\( \phi \rightarrow \phi – \frac{\partial \lambda}{\partial t} \)

voor de elektrische potentiaal, waarbij \( \lambda \) een functie is van de tijd- en ruimtecoördinaten, en

\( \textbf{A} \rightarrow \textbf{A} + \nabla \lambda \)

voor de magnetische potentiaal, waar \( \nabla \lambda \) wederom een gradiënt aangeeft: die van dezelfde functie \( \lambda \). De gecombineerde transformatie van allebei noemen we een ijktransformatie. Deze transformatie verandert zoals gezegd de elektromagnetische velden niet: als je de wiskunde netjes doorrekent zie je dat de transformaties van de verschillende termen in de gegeven definities van het elektrische en het magnetische veld elkaar precies opheffen.

Je vraagt je misschien af waarom we deze overbodigheden niet uit onze beschrijvingen halen. Waarom doen we zo veel moeite om deze ijksymmetrie te behouden? Kunnen we niet werken met een wiskundige beschrijving die alleen fysisch waarneembare grootheden bevat? Om te beginnen is het hebben van ijksymmetrie vaak erg handig. Je kan vaak wisselen tussen verschillende ‘ijkpunten’, waarbij bepaalde aspecten van een systeem, zoals een symmetrie, duidelijker zijn in één ijk, en andere aspecten duidelijker in de andere.

Bovendien blijkt dat ijksymmetrie je een heel eenvoudige manier geeft om allerlei dingen af te leiden die wél fysisch zijn: waarom bepaalde deeltjes massa hebben (het Higgs-mechanisme), het behoud van elektrische lading, of waarom fotonen massaloos zijn. Ook blijkt dat ijktheorieën wiskundig gezien extreem interessante objecten zijn. Behoud van lading bespreek ik hieronder; ik zal de andere onderdelen in vervolgartikelen beschrijven, die dit tweeluik in een serie zullen veranderen.

Koppelen aan een scalair veld en behoud van lading

Stel dat we naast de elektromagnetische velden ook een scalair veld \( \psi \) introduceren. Een “scalair veld” is wederom een functie van plaats en tijd, die overal een bepaalde waarde aanneemt maar niet, zoals een vectorveld, ook een richting. (Technisch gezien is het veld dat we nodig hebben een complex scalair veld, dat op elk punt de waarde van een complex getal geeft.) Als je de wiskundige beschrijving van al deze velden samen kiest op de eenvoudigste manier waarbij dit scalaire veld met de elektromagnetische velden een interactie heeft (de zogenaamde minimale koppeling) dan moet je om ijksymmetrie te behouden niet alleen de bovenstaande transformaties uitvoeren, maar ook de transformatie op het scalaire veld

\( \psi \rightarrow e^{-i q \lambda}\psi \)

waar \( q \) de elektrische lading is van dit veld. (Ook hier zijn technisch gezien weer complexe getallen nodig; dat zie je aan het getal \( i \) dat hier verschijnt.) Fysisch gezien betekent deze transformatie dat je de definitie van de eenheid van elektrische lading op elk punt op een andere manier verandert, omdat \( \lambda \) zoals we hebben gezien een functie van de locatie en tijd is. Dit noemen we een lokale transformatie. IJksymmetrie betekent hier dus dat je lokaal de definitie van lading mag aanpassen, zolang je maar een elektrische en magnetische potentiaal introduceert die op hetzelfde moment transformeren op de hierboven beschreven wijze. Deze potentialen houden dan als het ware bij hoe je de definitie van lading overal hebt veranderd en compenseren de wiskundige beschrijving daarvoor.

Als \( \lambda \) echter een constante functie van tijd en ruimte is, noemen we dat een globale transformatie. Zo’n globale ijksymmetrie vertelt ons dat er ook een bijbehorende “echte” symmetrie is: we kunnen ook in de fysische toestand dan alle ladingen aanpassen zonder dat er iets waarneembaars verandert. Echte symmetrieën zijn dus wel gerelateerd aan ijksymmetrieën! We kunnen hier in het bijzonder ook Noethers stelling toepassen: de invariantie van het systeem onder de bovenstaande transformaties in het globale geval leidt tot behoud van lading!

Dit is nog maar het topje van de ijsberg. In volgende artikelen zal ik bijvoorbeeld de gevolgen van zogenaamde asymptotische symmetrieën beschrijven. Dit zijn symmetrieën onder lokale transformaties zoals hierboven, maar waarbij de functie \( \lambda \) heel snel naar nul gaat wanneer je ruimtetijdcoördinaten groot maakt. Zoals we zullen zien zijn ook dit wel degelijk fysische transformaties. Ook zal ik de oorspronkelijke vraag van deze serie beantwoorden, namelijk waarom sommige deeltjes massa hebben en andere niet: een gevolg van het Higgsmechanisme. Ten slotte hoop ik nog eens een artikel te schrijven over de rijke connectie tussen ijktheorieën en topologie.

In de zomermaanden verschijnt op de QU-site wekelijks een artikel op vrijdag. Vanaf september publiceren we weer op elke dinsdag en vrijdag een artikel.