
1 What about photons?
Everybody knows the famous slogan: ”E equals m c squared”, or written in more mathematical form:
\( E = m c^2 \),
where E and m are the energy and mass of some object and c is the speed of light, which is an enormous number: c = 299792458 meters per second. On the one hand, this relationship between mass and energy is baffling, because it states that any object with a tiny amount of mass has a large energy content (because c is so big). On the other hand it is perhaps even more perplexing that this equation would mean that massless objects, like light, would have no energy at all.
That seems rather strange, because we all know that after a long sunbath on a hot summer day we get burned and this is certainly because the photons1 have deposited some energy on our skin.
So what happened here? Where is our mistake? Well, it’s simple – at least it was for Einstein…: we don’t have the full picture! We have forgotten a crucial part of the above equation, namely the part taking into account what happens to moving objects. As we all know, photons don’t like to stay long at parties. Usually when talking about movement we refer to the momentum p of an object. Including that, Einstein presented us with the full equation:
\( E^2 = (mc^2)^2 + (pc)^2 \).
Now we see that if something is not moving (meaning p = 0) we can take the square root and get back our ‘slogan’, but for objects without mass (m = 0) and with a nonzero momentum we get a new expression, which explains why sunbathing for long hours hurts: there is now a nonzero energy E = pc.
Take-home message: photons have energy even though they are massless. And even more importantly: put on sunscreen because of it.
2 Geometry of Einstein’s formula
The complete formula above is too long for a catchy slogan: ”E squared equals m times c squared all squared…bla bla”, but still there is a beautiful geometric structure in the formula itself, even if it is difficult to crunch into a slogan. The problem lies in all the squares. But we have seen such a formula in school before, just in a different light: it is the Pythagorean formula for right-angled triangles:
\( c^2 = a^2 + b^2 \),
where we can substitute c → E (hypotenuse), a → mc2 (opposite side) and b → pc (adjacent side) to get back Einstein’s complete formula!
Is there something behind this apparent structure and can we extract some physics from it? Indeed there is and (to copy the 44th President of the United States Barack Obama): yes we can! First we need to do something that is always helpful: make a drawing. Since we have seen that our old friend Pythagoras is hidden behind Einstein’s formula we may draw a triangle and label all sides as mentioned above:
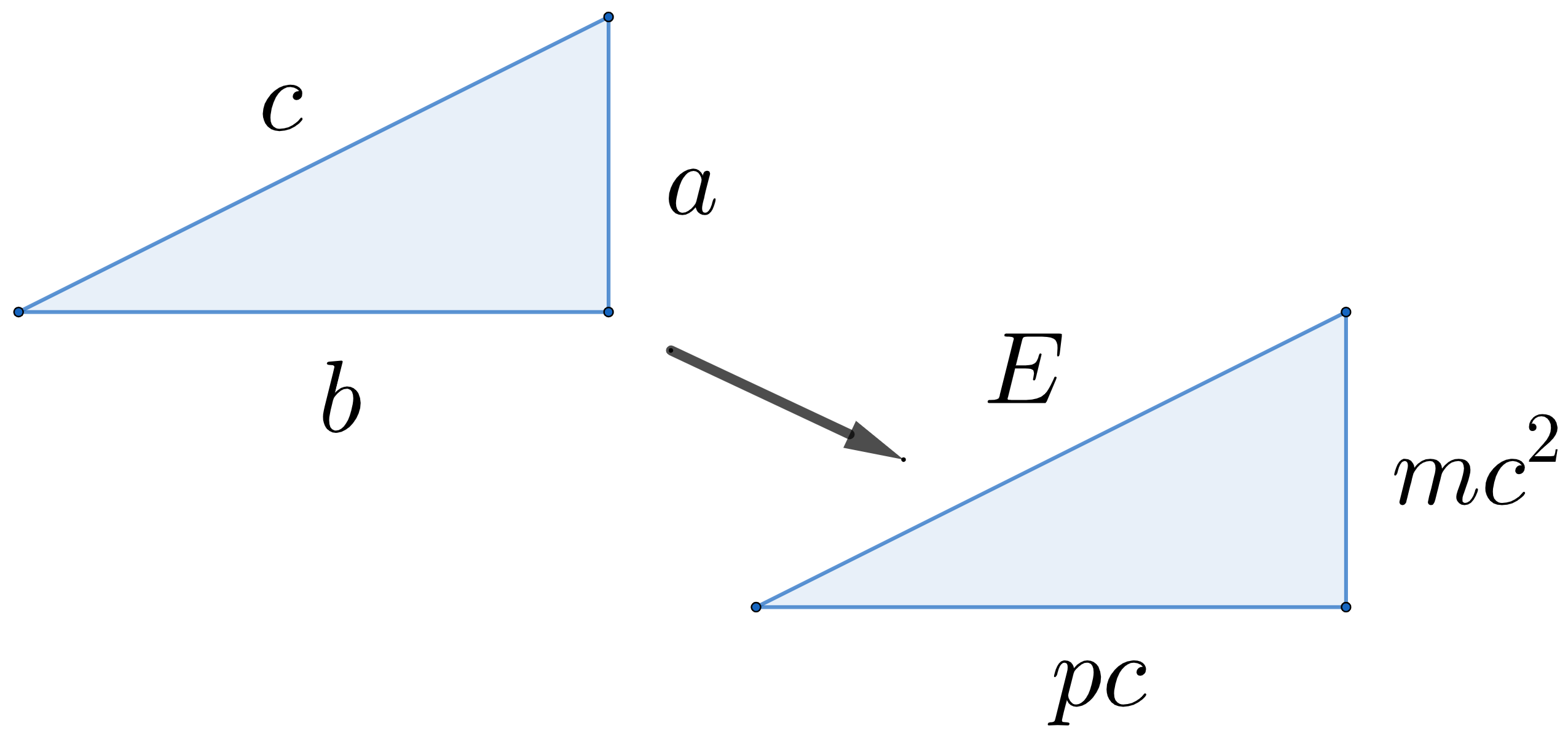
This representation helps us understand Einstein’s equation in all its facets. For example, in the cases where the momentum is zero or where the mass is zero, we just ”squeeze” the triangle into a line, where one then interpretsthe resulting blue line as an equality (”=”) between the hypotenuse and the adjacent or the opposite side.
Incredibly we get back our two friends from before: the famous slogan E = mc2 and the ‘sunbathing equation’ E = pc!
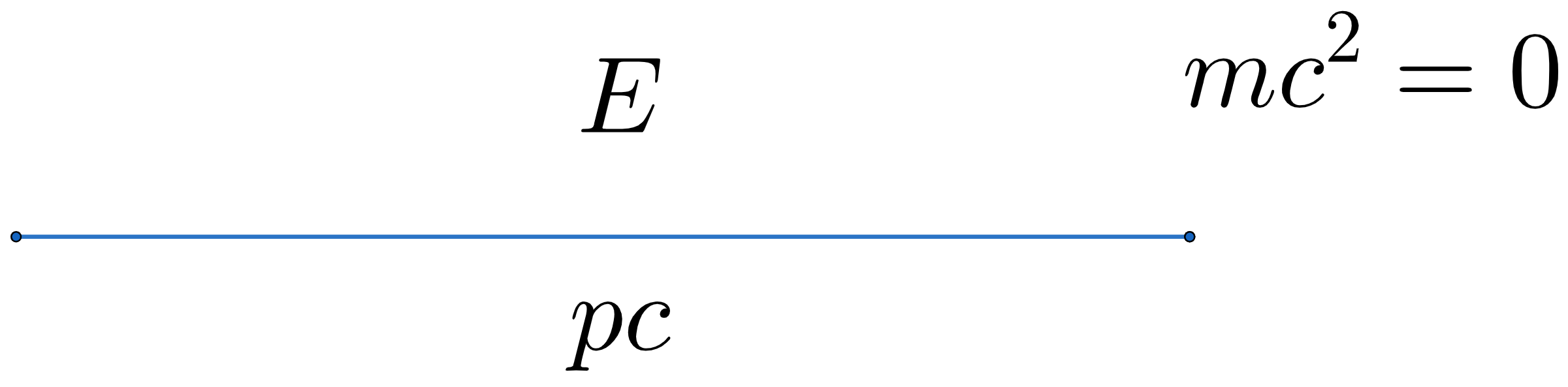
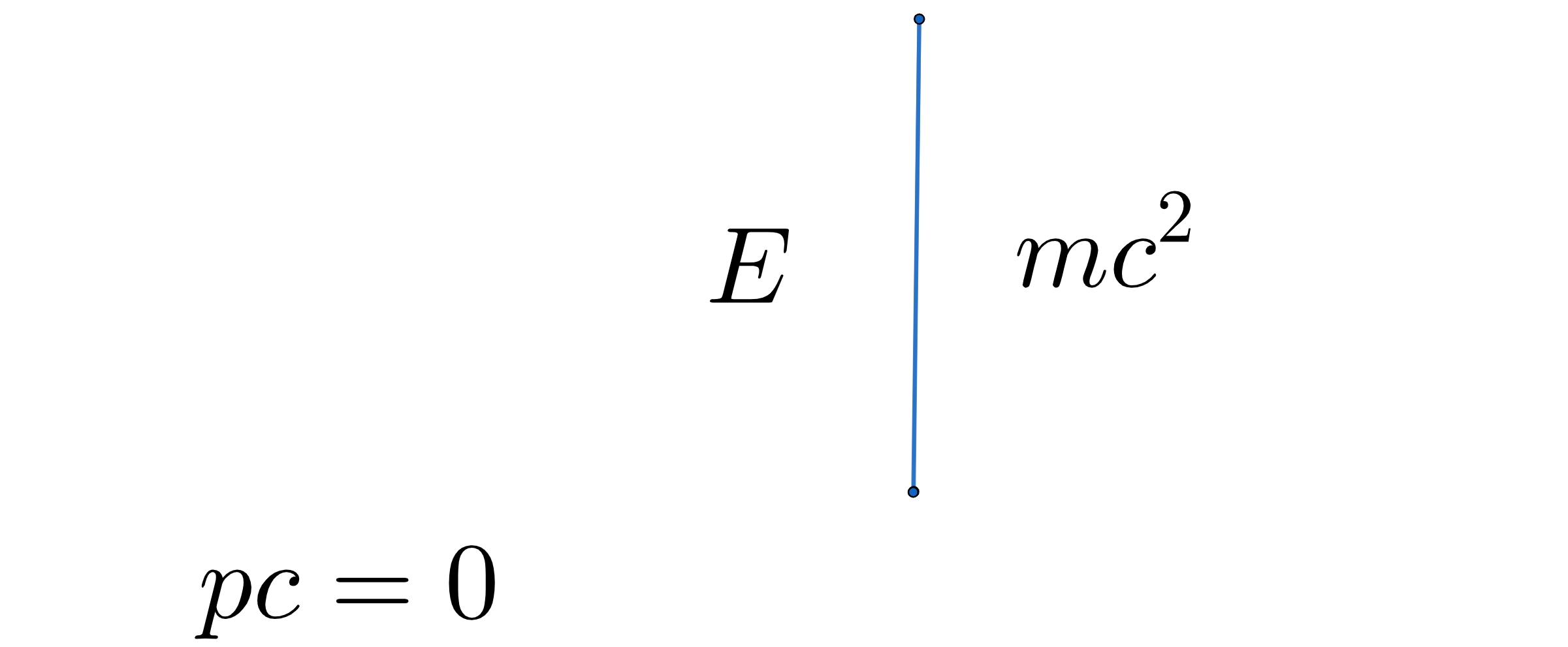
3 The universal speed sign: c
Now that we have established this representation to be appropriate for the description of Einstein’s formula we may want to see what else it illustrates. Let’s try to see what happens if we try to squeeze the hypotenuse into a horizontal line but without fully doing so. We would get something like the following:

You can see that as the two sides approach each other, the moving object that our equation describes will behave more and more like light, but not exactly, as there will always be a small little piece of mc2 hanging around at the other side.
What can we now extract from this? Well, we can see why nothing moves faster than the speed of light, which we denoted as c. It is exactly because the behaviour of anything with mass will never truly be the same as light, as seen by the triangle diagram! Let me explain this in a bit more detail.
In a more mathematical framework one can write the speed of an object in terms of the momentum and energy as follows 2
\( v = c \frac{pc}{E} \).
As the hypotenuse (E) is always bigger than the adjacent (pc), no matter how much it approaches the behaviour of light, it will result in pc/E < 1 (for massive particles) and hence
\( v < c \),
for objects with mass. In spite of everything you try to do, you will never exceed this cosmic speed limit set by the speed of light.
4 Recap
So here is what we have learned:
- We have seen that E = mc2 is not the full formula, because we forgot about the movement part of the equation leading us to Einstein’s formula: E2 = (mc2)2 + (pc)2
- Additionally we identified this equation with that of a triangle with hypotenuse E, adjacent side pc and opposite side mc2
- We have seen that squeezing that triangle depicts why massive objects cannot reach the speed of light c
Now that you have uncovered the secret behind the incompleteness of E = mc2 you have become a real physicist!
[1] Photons are the quantum particles of light.
[2] Just trust me on this one. Or if you are sceptical (which is good) look it up in any textbook covering Special Relativity. Keywords: ”relativistic energy”, ”relativistic momentum”.