
Het eenvoudigste model om zulke afhankelijke kansprocessen te beschrijven, is een markovketen, vernoemd naar de Russische wiskundige Andrey Markov, die in 1906 het eerste artikel hierover publiceerde. Kort samengevat beschrijft een markovketen een reeks van gebeurtenissen, waarbij de kans op een toekomstige gebeurtenis alleen afhangt van de huidige toestand van het systeem, en niet van het verdere verleden. Ondanks deze versimpelende aanname zijn markovketens krachtige wiskundige modellen met brede toepassingen in onder andere biologie, informatietheorie en natuurkunde. Hoe werkt zo’n markovketen precies?
Niets zo veranderlijk als het weer
Deze en volgende week ben ik in Zuid-Duitsland voor een PhD-zomerschool. Zondag hebben we een vrije dag, dus als het weer het toelaat, wil ik graag een stuk gaan wandelen. Uiteraard check ik verscheidene weersvoorspellingen, die allemaal gebruik maken van uitgebreide, en voor mij onbegrijpelijke, wiskundige modellen. Toch kan ik ook met een relatief eenvoudig model al een leuk inzicht krijgen in de weersverwachting. Voor het gemak neem ik aan dat er slechts drie weertypes bestaan: ‘zonnig’, ‘bewolkt’ en ‘regenachtig’. Uiteraard wordt mijn model nauwkeuriger als ik meer weertypes toevoeg, zoals ‘halfbewolkt’ en ‘sneeuw’, en rekening houd met verschillende windrichtingen en temperaturen, of met het feit dat één dag niet altijd maar één type weer heeft, maar het onderliggende idee van het model blijft hetzelfde.
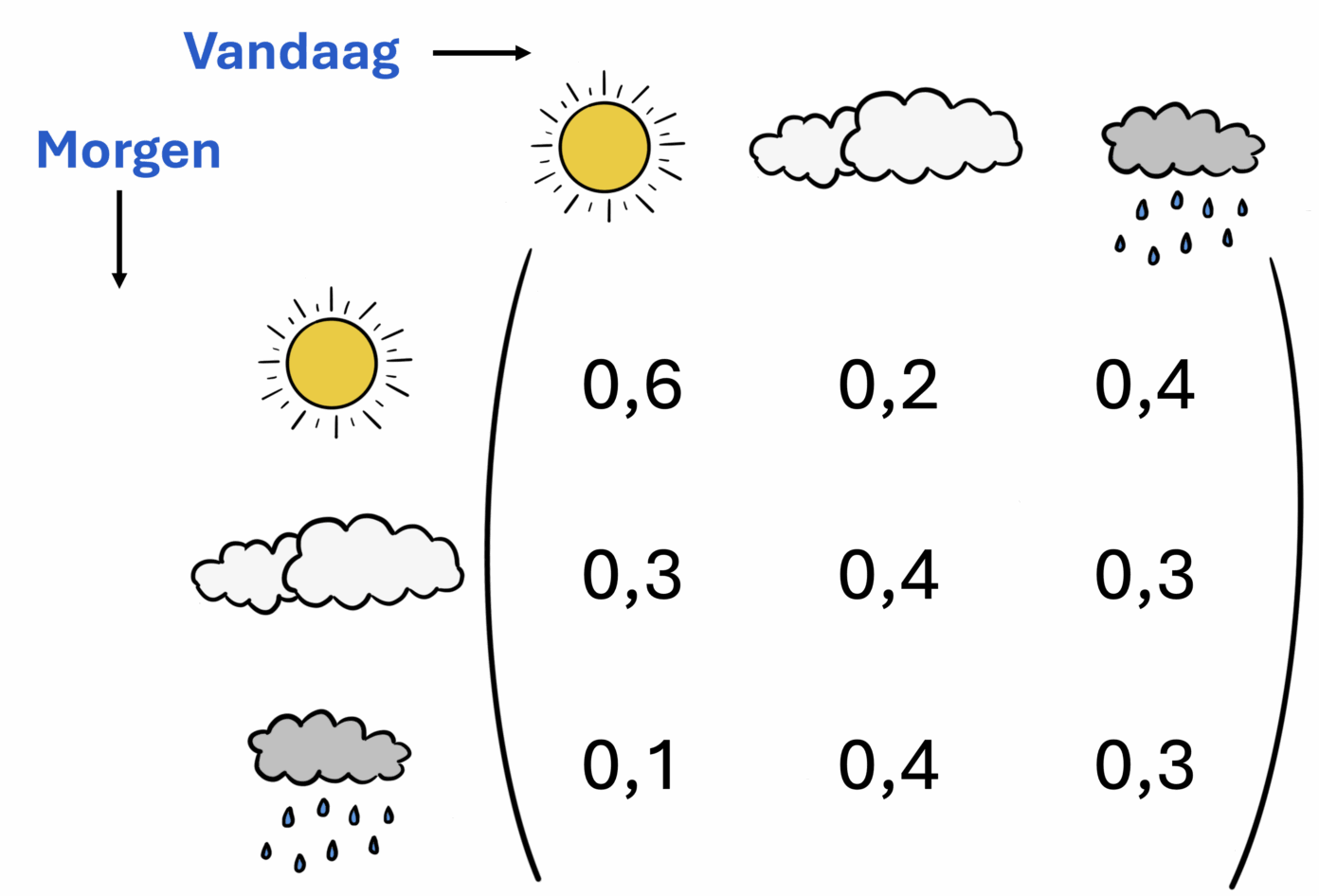
Als het vandaag zonnig is, is er een redelijke kans dat het morgen weer zonnig is, maar het kan ook bewolkt zijn of regenen. Als het vandaag regent, is er een vrij grote kans dat het morgen droog is. Een inschatting van de kans dat na een zonnige dag een bepaald weertype optreedt, kan worden gemaakt door te kijken naar weergegevens uit het verleden. Zo zou je hypothetisch gezien kunnen afleiden dat er na een zonnige dag 60 procent kans is dat het morgen zonnig is, 30 procent kans dat het morgen bewolkt is, en 10 procent kans dat het morgen regent. Op vergelijkbare wijze kun je de kansen afleiden voor het weer van morgen, gegeven dat het vandaag bewolkt dan wel regenachtig is. Het resultaat is een markovketen. Zo’n keten kan schematisch worden weergegeven zoals hieronder:

Vanuit de collegebanken zie ik dat het vandaag zonnig is, en vraag ik me af hoe groot de kans is dat het over twee dagen ook zonnig is en ik lekker kan gaan wandelen. En wat is de kans dat het volgende week vrijdag – terwijl ik in de trein naar huis zit – regent? Je kunt proberen om deze vragen te beantwoorden met behulp van het bovenstaande diagram, maar zult waarschijnlijk merken dat de berekeningen al snel erg onoverzichtelijk worden. ‘Over twee dagen zonnig’ zegt nog niets over het weer van morgen. Het kan drie dagen op rij zonnig zijn, maar het kan morgen ook bewolkt zijn of regenen, en overmorgen tóch weer zonnig zijn. Om de kans op een zonnige zondag te berekenen, moeten we met al deze mogelijkheden rekening houden. Voor twee dagen is dit misschien nog wel te doen, maar het aantal mogelijkheden neemt snel toe. Zo zijn er voor het weer van over een week al 37=2187 mogelijke reeksen van weertypes die we mee moeten nemen in de berekening!
Om al deze mogelijkheden op efficiënte wijze mee te nemen in de berekening, kun je gebruikmaken van een van de meest gebruikte gereedschappen in de wiskunde: een matrix. Een matrix is eigenlijk niets anders dan een tabel met getallen. De markovketen van afbeelding 1 kan beschreven worden met een matrix met 3 kolommen voor het weer van vandaag en 3 rijen voor het weer van morgen. De getallen in de matrix zijn de overgangskansen uit afbeelding 1. Het resultaat is hieronder weergegeven in afbeelding 2. Wat deze beschrijving in termen van matrices zo nuttig maakt, is dat matrices met elkaar – en met vectoren (matrices met één kolom) – kunnen worden vermenigvuldigd. Hoe dit precies in zijn werk gaat, is voor nu niet belangrijk. Het belangrijkste is dat het kán, en dat computers er heel goed in zijn.
De observatie dat het vandaag zonnig is, kan worden weergegeven met een vector met een één bovenaan en daaronder twee nullen: er is 100 procent kans op zon vandaag. Ik heb immers al vastgesteld dat de zon schijnt! Volgens onze versimpelde aanname dat er op een dag maar één weertype voorkomt is er bovendien vandaag dus 0 procent kans op bewolking of regen. Om de kansen voor het weer van morgen te bepalen, vermenigvuldig ik deze vector met mijn Markovmatrix. Het resultaat, de vector (0,6 , 0,3 , 0,1), wisten we natuurlijk al: dit zijn precies de kansen op zonnig, bewolkt en regenachtig weer, als het vandaag zonnig is. Om de kansen voor het weer van overmorgen bepalen, hoef ik nu alleen maar deze nieuwe vector nóg een keer te vermenigvuldigen met de markovmatrix, een klusje dat met de computer zo gepiept is. Het resultaat is dat er 46 procent kans op zon is, 33 procent kans op bewolking en 21 procent kans op regen. Niet slecht, al weet ik nog niet zeker of ik mijn regenjas thuis durf te laten!
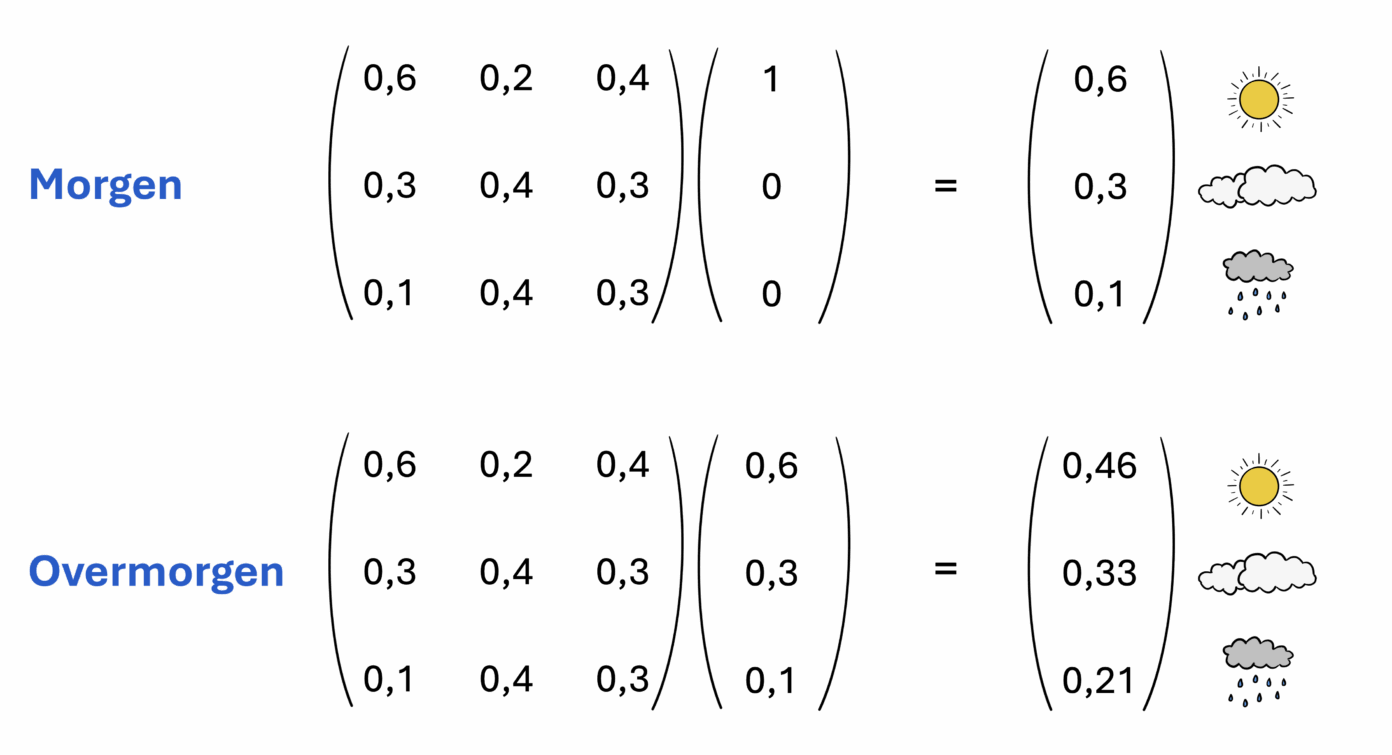
Voor het weer van volgende week, volgende maand, of zelfs volgend jaar, hoef ik alleen maar dezelfde vermenigvuldiging nog een aantal keer te herhalen. Het resultaat is een kansverdeling voor het weer in de toekomst. Als je ver genoeg in de toekomst kijkt, komt hier in veel gevallen een stabiele verdeling uit die niet afhangt van de toestand waarmee je begonnen bent (‘vandaag zonnig’) en die niet meer verandert als je nog een keer met de markovmatrix vermenigvuldigt (de voorspelling voor volgend jaar is hetzelfde als de voorspelling voor volgend jaar plus één dag). Voor de markovmatrix uit afbeelding 2 zegt deze stabiele verdeling dat op een dag ver in de toekomst er 42 procent kans is op zonnig weer, 33 procent op bewolking en 25 procent op regen.
Met dit eenvoudige weermodel kun je natuurlijk niet met zekerheid het weer in de toekomst voorspellen. Dat is een eigenschap die voor de meeste markovketens geldt. In veel toepassingen zijn het dan ook juist de statistische eigenschappen van de keten die belangrijk zijn.
De wiskunde van de atoombom
Een van de eerste grote toepassingen van markovketens was in het Manhattanproject, de destijds zeer geheime samenwerking tussen wetenschappers in de Tweede Wereldoorlog om de eerste atoombom te ontwikkelen. De werking van een atoombom is gebaseerd op kernsplijting: het uiteenvallen van een grote atoomkern in twee of meer kleinere atoomkernen en losse neutronen. Deze kernsplijting treedt bijvoorbeeld op wanneer een uranium-235-atoomkern – een uraniumkern met in totaal 235 protonen en neutronen – een extra neutron absorbeert. Hierdoor ontstaat een uranium-236-kern, die zeer onstabiel is, en snel vervalt in twee kleinere atoomkernen. Bij dit verval komen ook één of meer neutronen vrij. De vrijgekomen neutronen kunnen op hun beurt weer geabsorbeerd worden door andere uranium-235-kernen, en zo nieuwe kernsplijtingen in gang zetten. Wanneer iedere kernsplijting gemiddeld meer dan één nieuwe kernsplijting veroorzaakt, ontstaat een steeds groter wordende kettingreactie waarbij veel energie vrijkomt: een atoombom.
Een belangrijke vraag in de ontwikkeling van de atoombom was hoeveel uranium er nodig is om een bom te maken. Om deze vraag te beantwoorden probeerden wetenschappers het gedrag van de neutronen in de bom te begrijpen. Dit was een erg moeilijk probleem: een ‘gemiddelde’ atoombom bevat meer dan een quadriljoen uraniumkernen – een één met 24 nullen erachter – die bij splijting allemaal weer neutronen vrijlaten en zo nieuwe splijtingen kunnen veroorzaken. Het aantal mogelijke uitkomsten van de kernreacties is dus gigantisch, en het is onmogelijk om al die uitkomsten door te rekenen.
De oplossing voor dit probleem kwam van Stanisław Ulam. De Pools-Amerikaanse wiskundige lag niet lang voordat hij de oplossing bedacht een tijd in het ziekenhuis door een hersenontsteking. Tijdens zijn herstel speelde Ulam vele potjes patience, en hij begon zich af te vragen hoe groot de kans is dat een willekeurig geschud patiencespel kan worden gewonnen. Hoewel het spel patience relatief eenvoudig is, bleek al snel dat deze vraag heel moeilijk te beantwoorden is. Iedere volgorde van de kaarten levert namelijk weer een ander spel op. In plaats van een exacte berekening bedacht Ulam daarom een andere tactiek: hij speelde honderden spellen patience en hield bij hoe veel van die spellen hij won. Dit gaf hem een benadering van de kans dat een patiencespel kan worden gewonnen.
Terug aan het werk realiseerde Ulam zich dat de neutronen in een atoombom misschien op vergelijkbare manier benaderd konden worden door willekeurige uitkomsten te genereren. Collega-wiskundige John von Neumann zag onmiddellijk de potentie in dit idee, maar realiseerde zich ook dat er een belangrijk obstakel is: in tegenstelling tot de verschillende patiencespellen zijn de neutronen in een atoombom niet onafhankelijk. De beweging van een neutron hangt af van waar het zich bevindt en waar de andere deeltjes zich bevinden. Oftewel: het gedrag van het neutron wordt beïnvloed door wat er eerder is gebeurd. In plaats van willekeurige uitkomsten moest er dus een hele keten van gebeurtenissen worden gesimuleerd, waarin iedere stap de volgende stap beïnvloedt. Inderdaad, er was een markovketen nodig.
Markovketen-Monte Carlo
In vereenvoudigde vorm ziet de markovketen van Ulam en collega’s er als volgt uit. De reactie begint met een neutron dat zich vrij voortbeweegt. Het neutron kan vier mogelijke gebeurtenissen ondergaan. Als eerste kan het neutron botsen op een ander deeltje, afgestoten worden en verder reizen. In dit geval blijft het neutron zich dus vrij voortbewegen. Het neutron kan ook verdwijnen uit het systeem, ofwel doordat het geabsorbeerd wordt door een kern die niet splijt, ofwel doordat het simpelweg in een andere richting beweegt, weg van de atoomkernen. Ten slotte kan het neutron worden opgenomen door een uraniumkern die splijt en daarbij twee of drie nieuwe neutronen uitzendt. De nieuwe neutronen ondergaan vervolgens hun eigen keten aan gebeurtenissen. Schematisch ziet dit proces er als volgt uit.
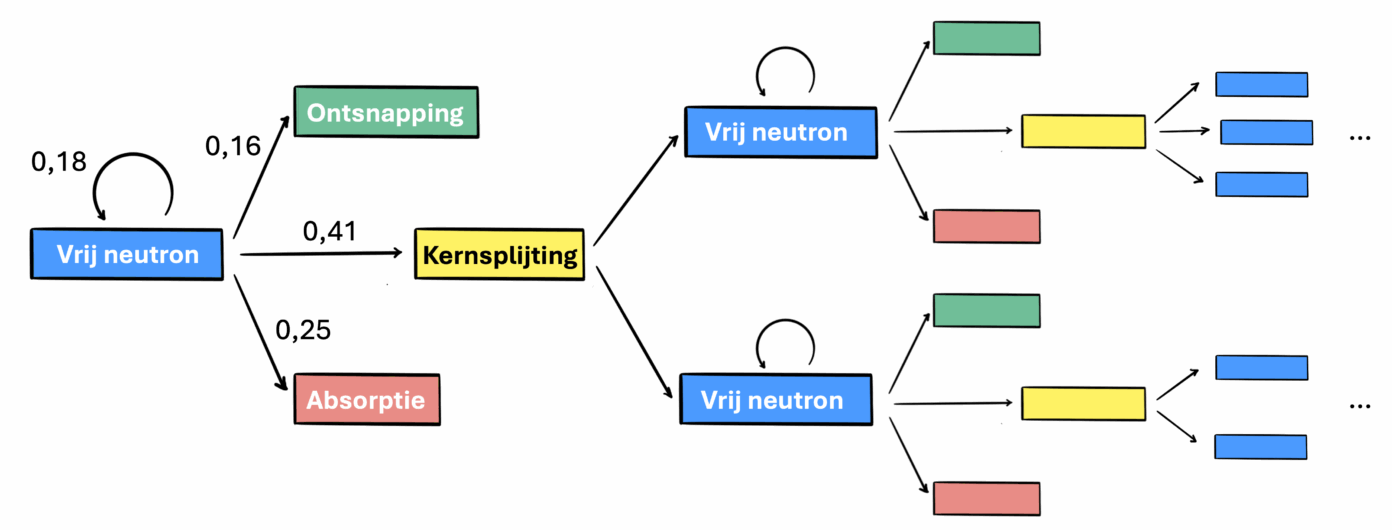
In tegenstelling tot het eenvoudige weermodel dat ik eerder besprak, liggen de overgangskansen in de neutronenketen niet vast, maar hangen ze af van bijvoorbeeld de positie en snelheid van de neutronen en van de hoeveelheid uranium die aanwezig is. De wetenschappers simuleerden de keten op de ENIAC, een van de eerste elektronische computers. Hiervoor lieten ze de computer een willekeurig neutron voor het begin van de keten generen. Vervolgens hielden ze in elke ronde bij hoeveel neutronen er bijkwamen en per keten (van een vast aantal stappen) bepaalden ze de vermenigvuldigingsfactor: het gemiddelde aantal nieuwe neutronen dat één neutron produceert. Door deze simulatie vele malen te herhalen, werd een statische verdeling van de uitkomst verkregen, vergelijkbaar met Ulams patience-uitkomsten en mijn weersvoorspelling voor de lange termijn. Als in de meeste simulaties de vermenigvuldigingsfactor kleiner is dan één, dan dooft de kettingreactie uit. Als de vermenigvuldigingsfactor groter is dan één, dan groeit de reactie steeds verder en heb je een bom.
Met deze methode kon dus een benadering worden gegeven van het aantal neutronen dat vrijkomt en het verloop van de kettingreactie, zonder exacte berekeningen te doen. De methode wordt de (markovketen) Monte Carlo-methode genoemd, naar het Monte Carlo-casino in Monaco. Het verhaal gaat dat Ulams oom daar pas was geweest, en dat Ulam het daar vaak over had tijdens zijn werk, omdat het probabilistische karakter van de methode hem deed denken aan het casino.
De wiskunde die bijna alles voorspelt
Ook vandaag de dag worden markovketens en Monte Carlo-methodes nog volop gebruikt. Ze helpen natuurkundigen om het gezamenlijke gedrag van vele deeltjes te bestuderen, scheikundigen om chemische reacties te begrijpen, biologen om populatiegroei te beschrijven en economen om financiële risico’s in te schatten. Ook jij maakt waarschijnlijk dagelijks gebruik van technologie die op deze wiskundige ideeën gebaseerd is, zoals zoekmachines en programma’s voor tekstvoorspelling. Wat ooit begon als een abstract idee, is nu een hulpmiddel dat ongemerkt in allerlei vakgebieden meedraait.
Wil je meer weten over het ontstaan van de markovketens en Monte Carlo-methodes of over hun hedendaagse toepassingen? Kijk dan vooral onderstaande video van Veritasium: