- Quantumzwaartekracht en oneindigheden
- Een niet-renormaliseerbare theorie
- Een formule voor de sterke kernkracht
- Van sterke kernkracht naar snaren

Afbeelding 1. Een snaar.Het idee achter de snaartheorie is dat de elementaire deeltjes in de natuur, wanneer we er voldoende sterk op inzoomen, minuscuul kleine, trillende snaartjes zijn.
Quantumzwaartekracht en oneindigheden
Snaartheorie is een theorie voor de quantumzwaartekracht. Wat houdt dat precies in, en wat is nu eigenlijk het probleem dat de snaartheorie oplost?
De quantummechanica is een theorie die drie van de vier natuurkrachten – de elektromagnetische kracht, de sterke kernkracht en de zwakke kernkracht – op de allerkleinste schaal met grote precisie beschrijft. Het wiskundige formalisme waarmee de theorie dit doet is nogal complex, maar de resultaten zijn dan ook indrukwekkend. De voorspellingen die de quantumfysica doet, komen tot op een groot aantal decimalen overeen met de experimentele waarnemingen. Het vervelende is dat datzelfde absoluut niet geldt voor de vierde natuurkracht: de zwaartekracht. Als we het wiskundige formalisme van de quantumfysica op de zwaartekracht loslaten, doet de theorie onzinnige voorspellingen. Vrijwel alle berekeningen aan experimenten rond de quantumzwaartekracht voorspellen oneindig grote meetwaarden!
Het probleem waar de quantumzwaartekracht mee kampt staat in vaktermen bekend als een UV-divergentie. De term ‘divergentie’ houdt in dat berekeningen een oneindige uitkomst krijgen; het voorvoegsel ‘UV’ zegt dat de problemen zich voordoen op heel kleine afstanden. Dit naar analogie van UV-licht: licht met heel korte golflengtes.
Er doet zich dus in de quantumzwaartekrachtberekeningen een oneindigheid voor die op heel korte afstanden ontstaat. Het zou te ver voeren om hier uit te leggen hoe die oneindigheid precies uit de wiskunde voortkomt, maar iedereen is bekend met een veel eenvoudiger voorbeeld waarin het gebruik van heel kleine getallen tot oneindig grote uitkomsten leidt: het door elkaar delen van twee getallen. Denk aan de bekende basisschoolwijsheid ‘delen door een breuk is vermenigvuldigen met het omgekeerde’. Een getal delen door 0,01 (1/100) is hetzelfde als het getal vermenigvuldigen met 100. Een getal delen door 0,001 (1/1000) is hetzelfde als het getal vermenigvuldigen met 1000, enzovoort. Hoe kleiner we het getal maken waardoor we delen, hoe groter de einduitkomst wordt. Vandaar ook de andere basisschoolwijsheid ‘delen door nul is flauwekul’: als we zouden proberen door 0 zelf te delen, zou de uitkomst oneindig groot worden.
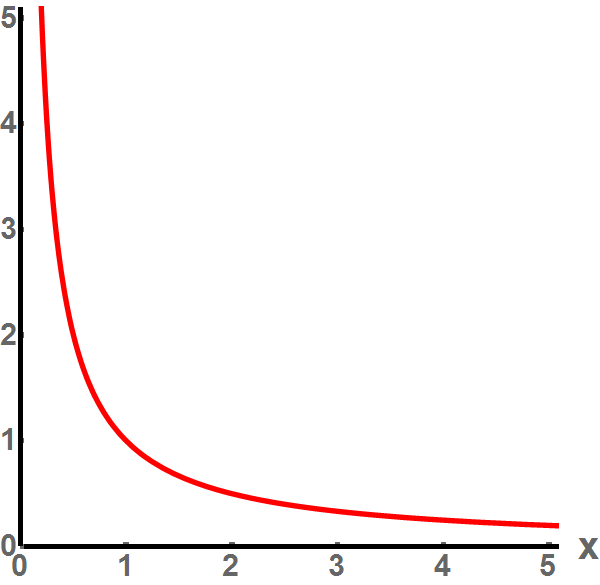
Afbeelding 2. Delen door nul is flauwekul.We zien de grafiek van de functie 1/x. Horizontaal staat de waarde van x uitgezet; verticaal de waarde van 1/x. Hoe dichter het getal x bij nul komt, hoe groter de waarde van 1/x wordt. Wanneer we door nul proberen te delen wordt het resultaat oneindig groot.
Het rekenprobleem in de quantumzwaartekracht is een gecompliceerdere versie van dit voorbeeld. Ook in quantumtheorieën komen kleine getallen voor: de deeltjes waarmee we rekenen zijn puntvormige deeltjes, die dus een grootte van 0 meter hebben. Dat wordt met name duidelijk als we in een diagram een quantummechanisch proces uitbeelden: zie afbeelding 3. (Een dergelijk diagram heet een Feynmandiagram – veel meer over zulke diagrammen valt te lezen in dit artikel.) We zien in het diagram de weg die een puntvormig deeltje zoals een elektron (rood) aflegt, terwijl het een ander puntvormig deeltje zoals een graviton (het deeltje dat de zwaartekracht overbrengt, blauw) uitzendt. De interactie tussen deze twee deeltjes vindt plaats in een punt, met grootte 0. Het is deze 0 die uiteindelijk in de quantumzwaartekrachtberekeningen tot oneindigheden leidt.
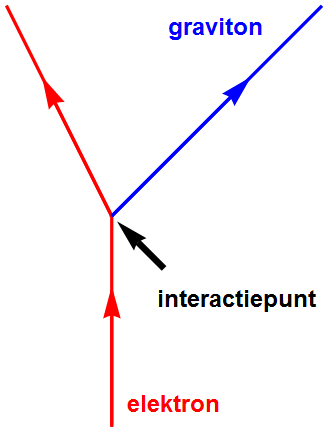
Afbeelding 3. Een eenvoudig Feynmandiagram.De rode lijn geeft de weg weer die een elektron aflegt. Op het interactiepunt zendt het elektron een graviton (zwaartekrachtsdeeltje) uit. Het interactiepunt heeft grootte nul.
Een niet-renormaliseerbare theorie
Overigens geldt wat we in de paragraaf hierboven hebben beschreven natuurlijk ook voor quantumtheorieën van andere puntdeeltjes. Ook daar komen interacties voor die plaatsvinden in een punt met grootte 0. Het verschil met de zwaartekracht is dat we voor de elektromagnetische kracht en de twee kernkrachten een andere wiskundige truc kunnen toepassen die het probleem verhelpt: de truc van renormalisatie. Ook over dit onderwerp is in een eerder dossier een uitgebreid artikel verschenen. Na het toepassen van deze truc blijken de oneindigheden als sneeuw voor de zon verdwenen, en geeft de theorie de genoemde uitkomsten die tot op grote precisie met de meetwaarden overeenkomen. Helaas werkt de truc van renormalisatie alleen niet voor de quantumzwaartekracht. Een quantumzwaartekrachtstheorie van puntvormige deeltjes leidt dus tot een groot wiskundig probleem, en dit is het probleem waar natuurkundigen nu al ruim een halve eeuw mee worstelen.

Afbeelding 4. Martinus Veltman en Gerard ’t Hooft.De Nederlandse natuurkundigen ’t Hooft en Veltman wonnen de Nobelprijs voor hun bijdrage aan de renormalisatie van de kernkrachten. Helaas werkt dezelfde renormalisatieprocedure niet voor een quantumtheorie van de zwaartekracht.
Uit de opbouw van ons verhaal hierboven lijkt een oplossing van het probleem voor de hand te liggen. We zouden de theorie van de quantumzwaartekracht zo willen aanpassen dat de interacties tussen deeltjes niet meer in een punt plaatsvinden. Daarvan uitgaande lijkt het idee van snaren in plaats van puntdeeltjes voor de hand te liggen, maar dat is natuurlijk achteraf geredeneerd. Historisch gezien werd het idee van snaren, zoals we hieronder zullen zien, pas na diverse toevalligheden en zijstappen ontdekt.
Een formule voor de sterke kernkracht
De geschiedenis van de snaartheorie begon in 1968, toen de Italiaanse natuurkundige Gabriele Veneziano een artikel publiceerde in het natuurkundetijdschrift Nuovo Cimento. Het onderwerp van dit artikel had niets te maken met de quantumzwaartekracht: Veneziano beschreef in zijn artikel een formule die gold voor de interactie tussen hadronen, deeltjes zoals het proton en het neutron die met elkaar wisselwerken door middel van de sterke kernkracht. De formule van Veneziano was puur empirisch: hij leidde die niet af uit dieper liggende grondbeginselen, maar schreef de formule alleen op omdat die de sterkte van de interactie tussen de verschillende hadronen goed leek te beschrijven.

Afbeelding 5. Gabriele Veneziano.Foto: CERN.
Veneziano’s formule sloeg niet erg aan in de theoretsiche-natuurkundewereld. De belangrijkste reden daarvoor was dat rond dezelfde tijd een andere theorie opkwam die de sterke kernkracht beschreef: de quantumchromodynamica, of kortweg QCD. Deze laatste theorie bleek de sterke kernkracht met erg veel precisie te beschrijven, waardoor een empirische formule zoals die van Veneziano niet meer nodig was.
Van sterke kernkracht naar snaren
De formule die Veneziano had ontdekt, verdween niet direct in de prullenbak. De reden daarvoor was dat er twee jaar na het artikel van Veneziano een vervolgartikel verscheen van de natuurkundigen Yoichiro Nambu, Leonard Susskind en Holger Nielsen. Waar Veneziano zijn formule op puur empirische gronden had opgeschreven, gaven Nambu, Susskind en Nielsen een afleiding van de formule uit dieper liggende grondbeginselen. Ze lieten zien dat de formule van Veneziano de interactie beschreef tussen deeltjes die op het microscopische niveau niet puntvormig waren, maar de vorm hadden van kleine ééndimensionale snaartjes: mini-elastiekjes in de vorm van kleine, gesloten lusjes.
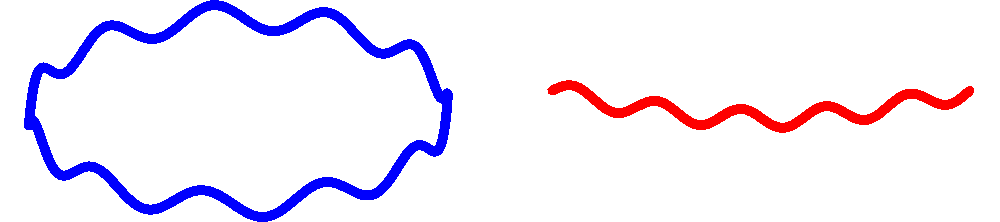
Afbeelding 6. Gesloten en open snaren.Snaren kunnen twee vormen hebben: gesloten (links) of open (rechts). De formule van Veneziano bleek gesloten snaren te beschrijven. We zullen in de komende twee artikelen zien welke rol open snaren spelen in de snaartheorie.
Daarmee was de vreemde situatie ontstaan dat er een formule was waarvan duidelijk was wat die beschreef, maar niet of en hoe die in de natuurkunde toegepast kon worden. Het zou nog een decennium duren voordat de formule van Veneziano in verband werd gebracht met de quantumzwaartekracht. Meer daarover valt te lezen in het volgende artikel in dit dossier.
In het vierde artikel in dit dossier zien we hoe de snaartheorie uiteindelijk een theorie van de quantumzwaartekracht werd.