Snaren en holografie (7): Compactificatie

In dit artikel:

• Tien dimensies
• Compactificatie
• D-branes of compactificatie?
• Een bug, of een feature?

Afbeelding 1. Een Calabi-Yauvariëteit.In dit artikel zullen we zien dat vormen zoals deze een belangrijke rol spelen in het vierdimensionaal maken van tiendimensionale snaartheorieën.

Tien dimensies

In het tweede artikel in dit dossier hebben we het uitgebreid gehad over dimensies. Onze natuur is driedimensionaal: om ergens te kunnen komen moeten we vooruit/achteruit, naar links/rechts en naar boven/beneden kunnen bewegen. Uit de relativiteitstheorie van Albert Einstein blijkt bovendien dat het nuttig is om ook de tijd als een dimensie te zien. We beschrijven de natuur dan niet meer aan de hand van ‘plaatsen’ met een x, y, en z-coördinaat, maar aan de hand van ‘gebeurtenissen’ met een x, y, z, en t-coördinaat. Op die manier bekeken is onze natuur dus vierdimensionaal. Om de speciale rol van de tijd in de notatie aan te geven, wordt ook wel gezegd dat onze natuur ‘(3+1)-dimensionaal’ is.

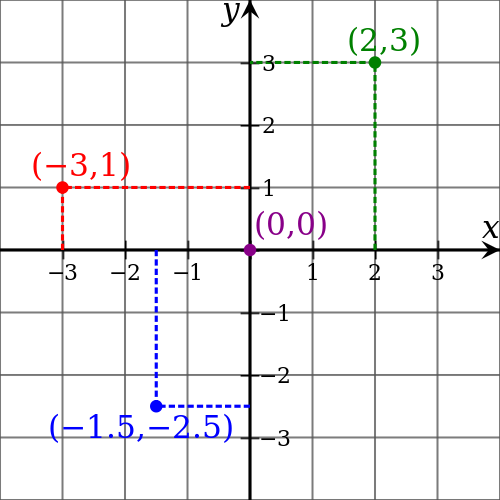
Afbeelding 2. Dimensies en coördinaten.Het aantal dimensies van een object of een ruimte is het aantal coördinaten dat we nodig hebben om een punt erin te beschrijven. Hierboven zien we een tweedimensionaal vlak, met een x– en een y-coördinaat. Om gebeurtenissen in onze natuur te beschrijven hebben we nog een derde ruimtecoördinaat en een tijdcoördinaat nodig.

De meeste natuurkundige modellen kunnen we in een willekeurig aantal dimensies gebruiken. Denk aan de mechanica van Newton: daarmee kunnen we even goed de beweging van biljartbalen over een tweedimensionaal laken, als de beweging van planeten in drie ruimtedimensies beschrijven. Er zijn echter ook natuurkundige modellen die alleen in een bepaald aantal dimensies werken. Met name in quantummechanische modellen is dat het geval. De reden daarvoor kwamen we in een eerder artikel al tegen: het bestaan van anomalieën. In quantummechanische theorieën is het begrip symmetrie erg belangrijk, en sommige quantumtheorieën leveren wiskundig onzinnige antwoorden op als bepaalde symmetrieën niet exact in de theorie aanwezig zijn. Dat levert vaak beperkingen op op het aantal dimensies waarin een model zijn werk doet: zo zijn er bijvoorbeeld natuurkundige modellen voor op het elektromagnetisme lijkende krachten die alleen in een even aantal ruimtetijddimensies blijken te werken.

In de snaartheorie blijken de beperkingen op het aantal dimensies nog sterker te zijn. Al vroeg in het onderzoek naar snaarmodellen werd duidelijk dat het alleen mogelijk is om een wiskundig consistente snaartheorie met alle vereiste symmetrieën op te stellen als die theorie een tiendimensionale ruimte beschrijft. Hierbij wordt de tijd weer meegeteld: we hebben het dus eigenlijk over een (9+1)-dimensionale ruimtetijd. Overigens werd oorspronkelijk ook een tweede mogelijkheid onderzocht: een theorie in (25+1) dimensies. Deze theorie bevat echter geen fermionische deeltjes (“harde” deeltjes zoals elektronen en quarks) en blijkt allerlei andere problemen met zich mee te brengen. Uiteindelijk waren het daarom alleen de vijf al genoemde, tiendimensionale snaartheorieën die alle selectiecriteria overleefden.

Naar boven

Compactificatie

Daarmee lijkt de snaartheorie in één klap volkomen nutteloos geworden voor het beschrijven van onze natuur. De natuur is immers (3+1)-dimensionaal in plaats van (9+1)-dimensionaal – we hebben maar liefst 6 dimensies te veel in onze theorie! Hoe kunnen die 6 dimensies er zijn als we ze niet zien?

Het antwoord blijkt in de vraag verscholen te liggen. Kunnen we niet op de één of andere manier ervoor zorgen dat we de overtollige 6 dimensies in de snaartheorie niet zien? Om iets te kunnen ‘zien’ (of meten) moet het groot genoeg zijn. Kunnen we dus niet 6 van de dimensies heel erg klein maken?

Afbeelding 3. Van twee dimensies naar één.Een tweedimensionaal kokertje gaat, als we het steeds strakker oprollen, steeds meer op een ééndimensionale lijn lijken.

Kijk bijvoorbeeld eens naar afbeelding 3. Bovenin de afbeelding zien we een kokertje – een tweedimensionaal vel papier dat is opgerold tot een buisje. Het buisje is nog steeds tweedimensionaal: een mier kan er in de lengterichting overheen lopen, maar kan ook rondjes om de cirkel lopen. Wanneer we nu echter het vel papier heel strak oprollen (of, wat bijna hetzelfde is, van enorm grote afstand naar het kokertje kijken) zien we dat het buisje steeds meer op een lijn gaat lijken. Effectief zien we dan dus een ééndimensionaal object. De tweede dimensie is wel aanwezig, maar is zo klein geworden dat we die niet zien.

Het op die manier ‘oprollen’ van dimensies in ons model wordt compactificatie genoemd. In het voorbeeld van het kokertje hebben we één dimensie opgerold tot een cirkel, maar we kunnen natuurlijk ook twee of meer dimensies compactificeren. Met meer dimensies kan dat bovendien op allerlei verschillende manieren. In afbeelding 4 zien we drie verschillende manieren om twee dimensies te compactificeren. Als we de figuren in die afbeelding heel klein maken, houden we een punt over: we hebben dan dus twee dimensies gecompactificeerd tot nul dimensies. Op soortgelijke manier kunnen we ook zes dimensies oprollen, en daarmee onze snaartheorie een natuur laten beschrijven die effectief vierdimensionaal is.

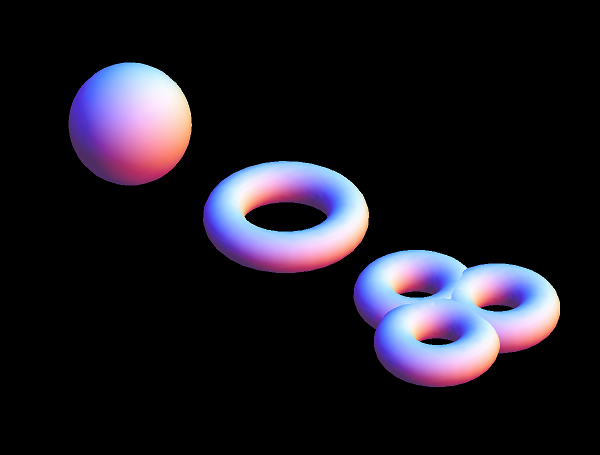
Afbeelding 4. Compactificatie van twee dimensies.Twee dimensies kunnen we op verschillende manieren ‘oprollen’: op een bol, een donut, of een vorm met meerdere ‘gaten’.

Naar boven

D-branes of compactificatie?

Wie het vorige artikel heeft gelezen, kan wellicht nog een tweede manier bedenken om met behulp van een tiendimensionale theorie een vierdimensionale wereld te beschrijven. In dat artikel zagen we dat er in een aantal snaartheorieën D-branes voorkomen: ‘membranen’ van een willekeurig aantal dimensies waarop de eindpunten van open snaren kunnen eindigen. We kunnen dus ook proberen om onze natuur in de (9+1)-dimensionale snaartheorie te beschrijven met behulp van een (3+1)-dimensionale D3-braan. We hebben gezien dat in de type IIB-snaartheorie inderdaad zo’n D3-braan kan voorkomen.

Dat dat idee nog niet zo gek is, zien we als we bedenken dat de open snaren die op een D3-braan eindigen inderdaad effectief maar in 3 dimensies kunnen bewegen. Ze kunnen weliswaar trillen in negen dimensies, maar doordat de eindpunten aan de D-braan vastzitten en de snaar zelf maar zo’n 10^-35 meter lang is, lijkt het op grote schaal alsof deze open snaren alleen maar langs de D3-braan kunnen bewegen. Dergelijke open snaren zouden dus prima de elementaire deeltjes in ons heelal kunnen beschrijven.

Afbeelding 5. Een snaar die op een D-brane eindigt.De snaar kan in alle ruimterichtingen trillen, maar kan alleen langs de D-braan over grote afstanden bewegen. Van grote afstand lijkt de snaar daarom op een puntdeeltje dat over de D-braan heen beweegt.

Een combinatie van de twee ideeën is natuurlijk ook mogelijk. Om een driedimensionaal heelal te beschrijven, kunnen we een D6-braan gebruiken (een object waarvan we gezien hebben dat het in de type IIA-snaartheorie voorkomt), en vervolgens nog 3 van de ruimtedimensies waarlangs deze D6-braan is uitgestrekt, oprollen. Ook dat levert weer open snaren op die op grote schaal gezien nog maar in 3 ruimterichtingen kunnen bewegen. Op minuscuul kleine schaal kunnen de snaren in al deze constructies echter nog steeds in 10 dimensies trillen, en dat blijkt voldoende te zijn om aan de consistentie-eisen die de wiskunde ons oplegt, te voldoen.

Naar boven

Een bug, of een feature?

Een interessante vraag is nu: op hoeveel verschillende manieren kunnen we zo uit een tiendimensionale snaartheorie een beschrijving van de vierdimensionale natuur maken? Dat aantal blijkt al snel gigantisch groot te zijn.

Laten we om te beginnen eens kijken naar het aantal manieren om zes dimensies op te rollen – dus nog zonder D-branen te gebruiken. Als we nog eens terugkijken naar afbeelding 4 zien we dat het oprollen van twee dimensies al op oneindig veel manieren kan: we kunnen van de twee dimensies een bolletje maken, of een donut-achtige vorm, of een vorm met drie ‘gaten’ – maar twee, vier of vijf gaten, enzovoort, kan natuurlijk ook. Dat levert al oneindig veel verschillende mogelijkheden, en we kunnen ons voorstellen dat de mogelijke variaties bij het oprollen van meer dan twee dimensies alleen maar toenemen.

Er blijkt een selectiemechanisme te zijn dat ons enigszins redt van deze oneindige keur aan compactificaties. We willen namelijk niet een willekeurig vierdimensionaal model uit de compactificatie krijgen, maar een model dat onze eigen natuur beschrijft. Ook hier speelt het begrip symmetrie weer een belangrijke rol: in onze vierdimensionale wereld zijn allerlei symmetrieën aanwezig, en we willen dat die symmetrieën ook gelden voor de gecompactificeerde snaartheorie. De belangrijkste symmetrie in dit opzicht is supersymmetrie: een symmetrie die, heel grofweg, zegt dat er in de natuur evenveel soorten bosonische als fermionische deeltjes zijn. Op alledaagse energieschalen zien we deze symmetrie niet, maar er zijn goede aanwijzingen voor het feit dat dat op de hoge energieschalen waar de snaartheorie een rol speelt, wel het geval is.

We willen de tiendimensionale theorie dus op zo’n manier compactificeren dat snaren uiteindelijk op evenveel manieren als bosonische deeltjes kunnen trillen, als als fermionische deeltjes. Dit blijkt een flinke beperking op te leggen aan de meetkundige ‘vormen’ die we kunnen gebruiken om de zes extra dimensies van de snaartheorie op te compacificeren. De vormen die aan deze eis voldoen heten Calabi-Yauvariëteiten, naar twee wiskundigen die deze vormen onderzochten. (‘Variëteit’ is het nette wiskundige woord voor wat we hier een ‘vorm’ hebben genoemd.)

Afbeelding 6. Een Calabi-Yauvariëteit.Het tekenen van zesdimensionale vormen is natuurlijk erg lastig; we zien hier een driedimensionale ‘doorsnede’ van een van de vele zesdimensionale Calabi-Yauvariëteiten. Zie afbeelding 1 voor een ander voorbeeld.

In hoeverre beperkt de eis van supersymmetrie bij hoge energieën de mogelijke manieren om snaartheorieën vierdimensionaal te maken? In zekere zin is de beperking gigantisch: van de oneindig veel mogelijkheden lijkt uiteindelijk nog maar een eindig aantal te voldoen. Aan de andere kant is het eindige aantal dat overblijft nog altijd gigantisch groot. Het precieze aantal is niet bekend, maar de snaartheoreet Michael Douglas heeft aangetoond dat een bepaalde klasse van compactificaties (inclusief D-branen) van de type IIB-snaartheorie leidt tot een aantal verschillende modellen met al tenminste 500 cijfers…

Aan de ene kant is deze veelvoud aan mogelijkheden erg positief: elke verschillende compactificatie van de snaartheorie leidt tot snaren die op andere manieren kunnen trillen, en daarmee uiteindelijk tot verschillende natuurwetten in vier dimensies. De kans is dus groot dat één van die vele mogelijkheden leidt tot een model waarmee we inderdaad onze natuur kunnen beschrijven.

Aan de andere kant kunnen we ons afvragen of een getal van tenminste 500 cijfers ons niet té veel mogelijkheden biedt. Als dat getal zo groot is dat we in feite elke ‘natuurkunde’ kunnen modelleren die we maar willen, verliest de snaartheorie volledig haar voorspellende waarde. Bijvoorbeeld: als uit metingen blijkt dat een bepaalde natuurconstante ongeveer de waarde 3,768 heeft, zijn er snaarmodellen die de waardes 3,7681, 3,7682, 3,7683, enzovoort voorspellen. We kunnen dus nooit uit de theorie bepalen wat het volgende cijfer in de waarde van de constante zal zijn, en daarmee kunnen we ook niet bepalen of een bepaald model dat we gekozen hebben daadwerkelijk onze natuur beschrijft.

Dit probleem staat bekend als het landscape problem (omdat er een bijna oneindig ‘landschap’ van verschillende modellen is om uit te kiezen) en het heeft geresulteerd in de nodige kritiek op de snaartheorie. Of die kritiek zal leiden tot het einde van snaarmodellen als beschrijving van onze natuur zal moeten blijken: het is niet uitgesloten dat er verdere consistentie-eisen zijn die het getal van 500 cijfers nog veel verder inperken, of dat bepaalde eigenschappen van onze natuur maar in een heel klein deel van de modellen blijken voor te komen.

Afbeelding 7. The trouble with physics.Het bestaan van een overdaad aan snaartheorie-compactificaties heeft geleid tot de nodige kritiek op de theorie. In het boek ‘The trouble with physics’ legt de natuurkundige Lee Smolin uit wat het probleem is, en waarom dat volgens hem betekent dat de snaartheorie nooit een volledige beschrijving van de natuur zal zijn.

Het bouwen van een zo goed mogelijk model van onze natuur aan de hand van de snaartheorie is een actief onderzoeksgebied waarin nog regelmatig vorderingen worden gemaakt. Dat onderwerp is echter niet waar we ons in de rest van dit dossier mee bezig zullen houden: voor ons is het voldoende om te weten dat al die snaarmodellen zowel de quantummechanica als de zwaartekracht omvatten. Los van de vraag of het met zo’n model lukt om de hele natuur te beschrijven, is het dus al heel interessant dat het de snaarmodellen überhaupt lukt om die twee tot voorheen zo tegenstrijdige theorieën samen te voegen. De vraag die ons in de rest van dit dossier zal bezighouden, is hoe dit kan, en welke algemene lessen we daaruit kunnen leren over de quantumzwaartekracht.

Een deel van de afbeeldingen uit dit artikel is eerder gepubliceerd in het boek ‘Snaartheorie‘ van de auteur.

In het achtste artikel in dit dossier zien we dat de vijf snaartheorieën gerelateerd zijn door diverse dualiteiten, en zo uiteindelijk allemaal dezelfde natuurkunde beschrijven.