Afbeelding 1. Wat is snaartheorie? Het vervangen van puntdeeltjes door snaren is slechts een eerste kleine stap op weg naar een interessante theorie van de natuur. In dit artikel bespreken we wat de volgende stappen zijn, en welke beperkingen we daarbij tegenkomen. Cartoon van Randall Munroe voor xkcd.com.
Wat is een snaartheorie?
Voor we ons bezighouden met de vraag of snaren ook open kunnen zijn, beantwoorden we eerst een algemenere vraag: wanneer is een theorie een ‘goede’ snaartheorie? Het idee om puntdeeltjes in onze beschrijving van de natuur te vervangen door kleine trillende elastiekjes lijkt in zekere zin nogal ad hoc. Waarom zouden we niet even goed kunnen aannemen dat de deeltjes in onze natuur kleine donuts, bananen of ruimteschepen zijn? Wat maakt een snaartheorie een goede kandidaat voor het beschrijven van de natuur? Een eerste antwoord op die vraag is het antwoord dat we in de vorige twee artikelen hebben beschreven: snaartheorie slaagt erin om de quantummechanica en de relativiteitstheorie aan elkaar te koppelen – een prestatie die vrijwel geen enkele andere theorie tot nu toe heeft weten te evenaren.
Daarmee zijn we er echter nog lang niet. Om te ontdekken of snaartheorie daadwerkelijk onze natuur beschrijft, moeten drie belangrijke stappen gezet worden. Allereerst is het gebruik van snaren als fundamentele deeltjes in zekere zin maar één ingrediënt: we moeten ook exact beschrijven hoe deze snaren met elkaar wisselwerken, welke soorten snaren er kunnen zijn (open, gesloten, en al dan niet voorzien van verdere eigenschappen), en op welke manier deze snaren kunnen trillen. Voor zo’n volledig ‘recept’ is dan de vraag: is een dergelijke snaartheorie wiskundig consistent? We hebben in de afgelopen artikelen al diverse voorbeelden gezien van manieren waarop een op het oog mooie natuurkundige theorie tot allerlei wiskundige problemen kan leiden. Zulke problemen uiten zich meestal in het verschijnen van de uitkomst ‘oneindig’ in berekeningen aan natuurkundige processen.
Lukt het om een dergelijke, wiskundig consistente theorie op te stellen, dan is de tweede vraag of we iets aan deze theorie hebben wanneer we onze natuur willen beschrijven. Beschrijft de theorie deeltjes die we, eventueel na het vastleggen van bepaalde vrije parameters in de theorie zoals de lengte van de snaren, kunnen interpreteren als de deeltjes die we in de wereld om ons heen aantreffen? Is het bovendien mogelijk om met de theorie de waargenomen interacties tussen die deeltjes te beschrijven?
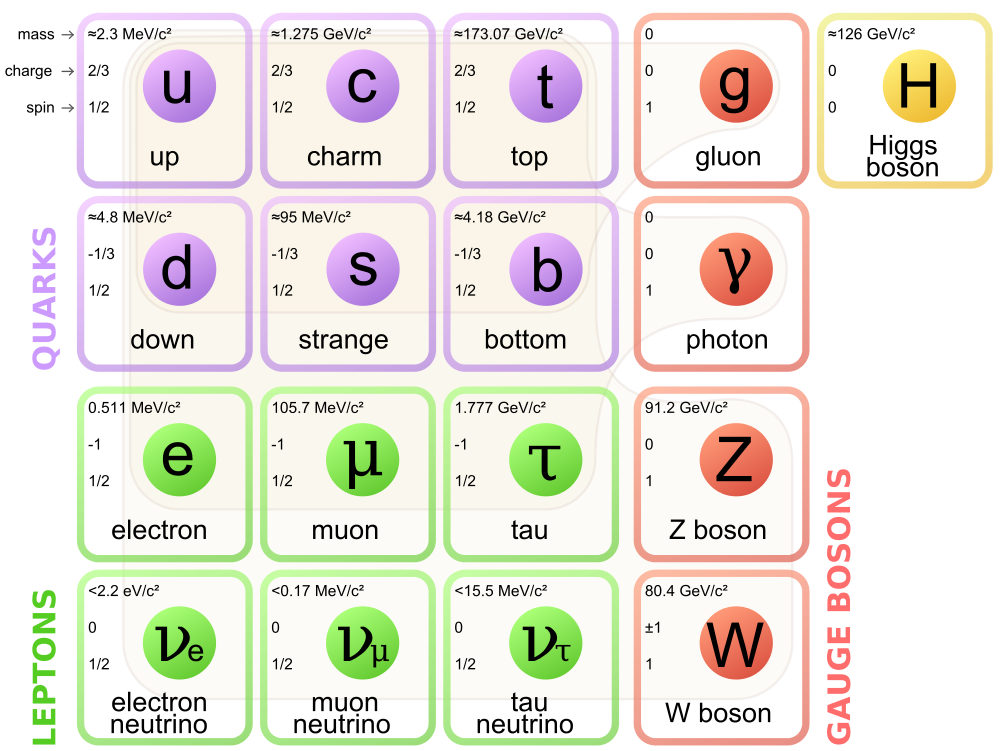
Afbeelding 2. Het standaardmodel van de elementaire deeltjes.Om een goede theorie van de natuur om ons heen te zijn, moet een snaartheorie in elk geval de verschillende deeltjes uit dit model en hun onderlinge wisselwerkingen kunnen beschrijven. (Zie ook het artikel over het standaardmodel uit ons dossier over quantumfysica.) Afbeelding: Wikipedia-gebruiker MissMJ.
Als blijkt dat onze kandidaat-snaartheorie inderdaad een kans maakt om onze natuur te beschrijven, is het tijd voor de derde en misschien wel belangrijkste stap: experimentele bevestiging. Voorspelt de theorie iets dat andere theorieën niet voorspellen, en kunnen we door middel van een experiment deze voorspelling testen? Pas als dat lukt, maakt een snaartheorie aanspraak op de titel ‘beschrijving van onze natuur’.
Van de drie hierboven beschreven stappen zullen we ons in dit artikel en het volgende met name met de eerste bezighouden: hoe kunnen we het idee van snaren gebruiken om wiskundig consistente theorieën van snaardeeltjes op te stellen? De tweede vraag – of die theorieën ook een kans maken om onze natuur te beschrijven – zal in de daaropvolgende artikelen nog volop aan bod komen. Wat de derde vraag, naar een experimentele verificatie van de snaartheorie, betreft: die vraag behandelen we maar kort, aan het eind van dit dossier. De eenvoudige reden daarvoor is dat de snaartheorie op dit moment nog niet ver genoeg is ontwikkeld om dergelijke experimentele voorspellingen te doen. Over de consistentie van snaarmodellen en de manier waarop we ze kunnen gebruiken om de natuur te beschrijven, valt echter veel meer te zeggen.
Vijf snaartheorieën
Laten we terugkeren naar de vraag waarmee we dit artikel begonnen. Het lijkt op het eerste gezicht voor de hand te liggen dat er twee soorten snaartheorieën opgesteld kunnen worden: een theorie van gesloten, lusvormige snaren, en een theorie van open, vetervormige snaren. Zoals we hierboven hebben besproken, is de werkelijke situatie echter veel ingewikkelder. We moeten ook vastleggen of het bijvoorbeeld mogelijk is om gesloten snaren open te breken tot open snaren, op welke manieren de snaren precies kunnen trillen, enzovoort.
Wat de eerste vraag betreft: het blijkt wel mogelijk te zijn om een theorie op te stellen van gesloten snaren die nooit ‘opengebroken’ kunnen worden, maar het omgekeerde is niet het geval. Een wiskundig consistente theorie waarin open snaren voorkomen, blijkt altijd de mogelijkheid te moeten bieden om de eindpunten van dergelijke snaren ‘aan elkaar te lijmen’ en zo gesloten snaren te vormen. Dat resultaat is niet heel verrassend: om interacties tussen open snaren te beschrijven (zie afbeelding 3) moeten we het eindpunt van één snaar vastplakken aan het beginpunt van een andere snaar. Maar hoe ‘weet’ het ene eindpunt dat het eindpunt dat het tegenkomt dat van een andere snaar is, en niet van zichzelf? Het blijkt onmogelijk deze kennis op een wiskundig consistente manier in de theorie in te bouwen, en dus kan elk eindpunt met elk beginpunt samensmelten – ook met het beginpunt van dezelfde snaar, waarbij dus een gesloten snaar wordt gevormd.
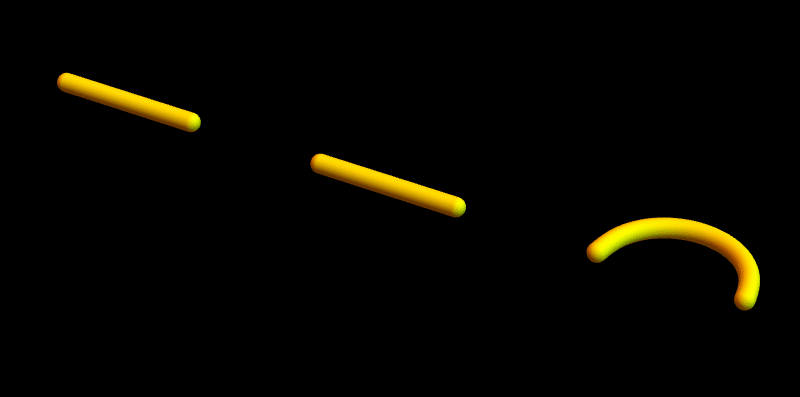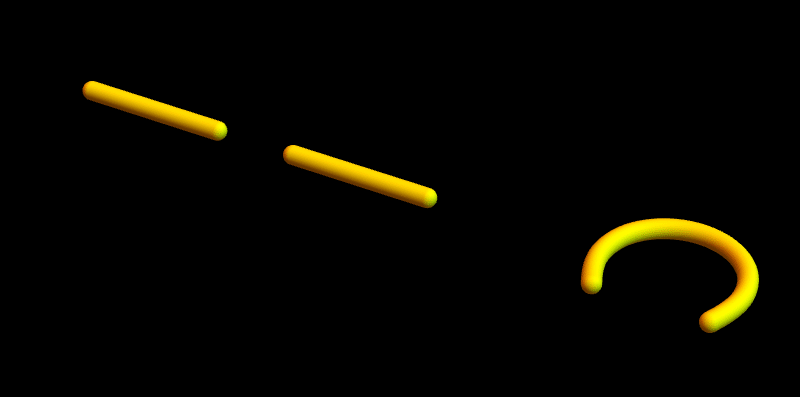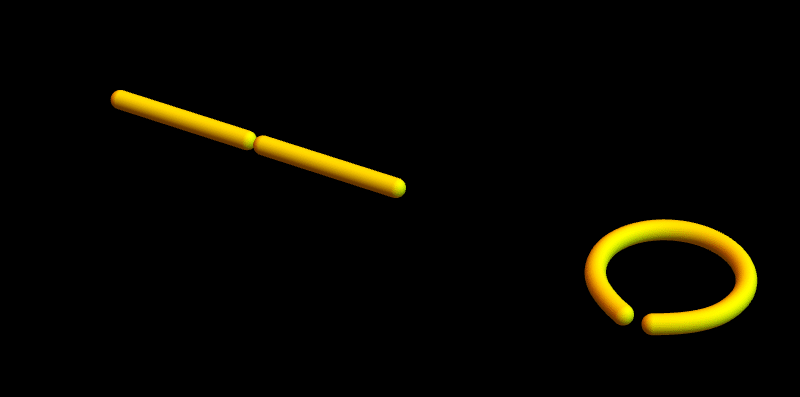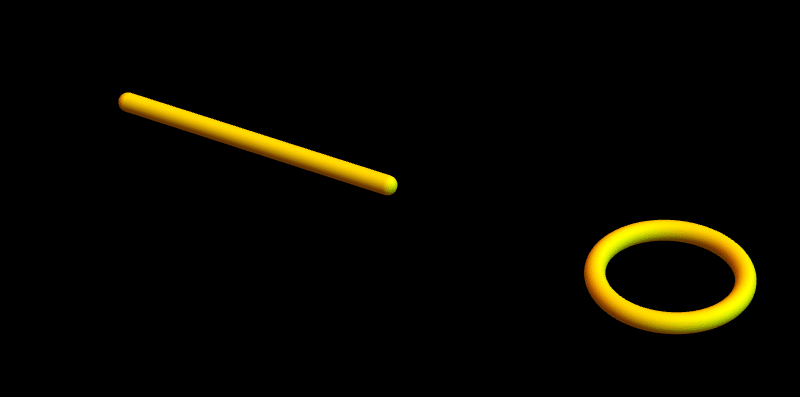
Afbeelding 3. Interacties tussen snaren.
Links zien we twee snaren die elkaar tegenkomen en samen één nieuwe snaar vormen. (Om de afbeelding eenvoudig te houden zijn de trillingen in de snaar niet getekend – de snaren zijn daarom rechte staafjes.) Rechts komt een eindpunt van een snaar het andere eindpunt van dezelfde snaar tegen. De eindpunten die elkaar tegenkomen ‘weten’ niet of ze tot dezelfde snaar behoren of niet; daarom moet de interactie rechts ook mogelijk zijn, en bevat een theorie van open snaren met interacties dus ook gesloten snaren.
Een aanvullende opmerking hierover: in de alinea hierboven spreken we van begin- en eindpunten, maar de vraag is natuurlijk of er een verschil is tussen die twee. Als we een schoenveter bestuderen, is er geen enkele reden om het ene uiteinde een beginpunt te noemen en het andere uiteinde een eindpunt: de twee zijn exact hetzelfde. Bestuderen we daarentegen een tuinslang waardoor water stroomt, dan is er een duidelijk beginpunt (waar het water de slang in komt) en een duidelijk eindpunt (waar het water de slang weer verlaat). Moeten we snaren vergelijken met schoenveters of met tuinslangen waarin water stroomt? Beide versies blijken mogelijk te zijn: er zijn geörienteerde snaren die een specifiek begin- en een specifiek eindpunt hebben, en ongeörienteerde snaren waarvan de twee uiteindes volkomen gelijkwaardig zijn. Ook gesloten snaren kunnen een oriëntatie hebben: we kunnen ons die orientatie voorstellen als een pijltje langs de snaar die een richting aangeeft.
Dan is er de vraag op welke manieren snaren precies kunnen trillen. Zoals we in het vorige artikel al beschreven, bepaalt het trillen van de snaar de eigenschappen van het deeltje dat we waarnemen. Een eenvoudig voorbeeld daarvan kwam in dat artikel al ter sprake: hoe meer een snaar trilt, hoe meer energie de snaar met zich meedraagt, en (dankzij Einsteins E=mc2) hoe zwaarder het snaardeeltje daardoor lijkt te zijn. De manier waarop de snaar trilt, blijkt echter nog veel meer eigenschappen van het deeltje te bepalen: bijvoorbeeld of een snaar een fermion of boson is. Ter herinnering: fermionen zijn de ‘harde’ deeltjes waaruit alle materie om ons heen is opgebouwd; bosonen zijn de ‘zachte’ boodschapperdeeltjes die zorgen voor het overbrengen van de verschillende natuurkrachten. Meer over bosonen en fermionen valt te lezen in dit artikel; voor nu volstaat de opmerking dat het hier gaat om twee heel verschillende types deeltjes, en dat de manier van trillen bepaalt of de snaar fermion of een boson is.
Uit de voorbeelden hierboven moge duidelijk zijn dat er veel meer mogelijkheden zijn voor het opstellen van een snaartheorie dan de eenvoudige keuze tussen open en gesloten snaren. Het aantal mogelijkheden lijkt misschien zelfs overweldigend groot, maar de vraag is natuurlijk: welke van deze mogelijkheden leiden tot een wiskundig consistente theorie? Die vraag was een belangrijke onderzoeksvraag voor snaartheoreten in de jaren ’80. Het antwoord dat uiteindelijk na veel studie gevonden werd, was verrassend: er bleken precies vijf wiskundig consistente snaartheorieën te zijn. De legio andere mogelijkheden die er bij het opstellen van de theorie zijn, leiden allemaal tot oneindigheden en andere wiskundige problemen; alleen deze vijf leken volledig waterdicht.
Eén eigenschap die alle vijf deze theorieën gemeen hebben, is dat ze allemaal supersymetrisch zijn – een kreet die grofweg inhoudt dat de snaar op precies evenveel manieren als fermion kan trillen, als als boson. (Deze beschrijving is erg kort door de bocht – over supersymmetrie valt veel meer te vertellen. Zie bijvoorbeeld de lezing van James Gates over dit onderwerp die we recent op deze website plaatsten.) Hoewel de details van de vijf consistente snaartheorieën in de rest van dit verhaal geen belangrijke rol spelen, geven we voor de volledigheid een overzicht. De vijf theorieën vallen uiteen in drie verschillende klassen, en kregen uiteindelijk de volgende, weinig inspirerende namen:
- Type I-snaartheorie. Een supersymmetrische theorie van ongeörienteerde, open (en gesloten) snaren.
- Type II-snaartheorie. Een supersymmetrische theorie die op het eerste gezicht (maar zie verderop!) alleen gesloten snaren leek te beschrijven. Deze snaren zijn georiënteerd. Er blijken twee varianten op deze theorie te zijn, die verschillen in de manier waarop de bosonische en fermionische trillingen met elkaar gematcht worden om een supersymmetrisch resultaat te krijgen. Om deze twee theorieën te onderscheiden spreken we van type IIA en type IIB.
- Heterotische snaartheorie. Zodra een snaar georiënteerd is, is het ook mogelijk om in de ene richting van de snaar andere trillingen te laten lopen dan in de andere. Het blijkt niet erg eenvoudig om dit te doen: de wiskunde achter de snaartheorie is erg gesteld op symmetrie, en zodra we proberen dergelijke asymmetrisch trillende snaren te construeren, leidt dat al snel tot inconsistenties en oneindigheden. Uiteindelijk bleken er slechts twee consistente mogelijkheden te zijn, waarin de trillingen die de ene kant op door de snaar lopen bosonisch en fermionisch zijn en voor beide theorieën exact hetzelfde, en de trillingen die de andere kant op door de snaar lopen alleen bosonisch en voor beide theorieën verschillend. De naam voor deze verschillende trillingen kwam voort uit hun wiskundige beschrijving, en leidde tot de namen van de twee snaartheorieën zelf: ze worden ‘SO(32)-heterotische snaren’ en ‘E8 × E8-heterotische snaren’ genoemd. Beide theorieën beschrijven alleen gesloten snaren.
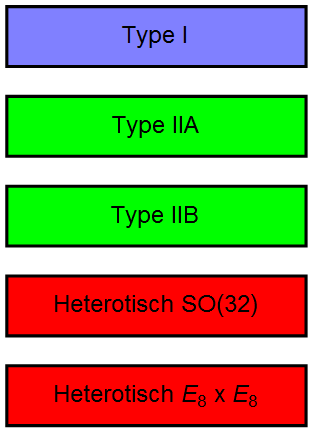
Afbeelding 4. Snaartheorieën.De vijf wiskundig consistente snaartheorieën.
Vier tegen één?
Het overzicht hierboven lijkt sterk in het voordeel van de gesloten snaren: alleen de type I-theorie bevat op het eerste gezicht open snaren. De andere vier theorieën beschrijven verschillend trillende gesloten snaren. Deze beschrijving blijkt echter wat te kort door de bocht: via een achterdeur is het toch mogelijk om ook in de twee type II-theorieën open snaren op te nemen. We zullen in het volgende artikel zien hoe dit mogelijk is, en waarom dat ook heel belangrijk blijkt te zijn: het zijn uiteindelijk namelijk de open snaren die zullen leiden tot het holografische principe!
Het zesde artikel in dit dossier gaat over de verrassende ontdekking dat er naast gesloten en open snaren nog heel andere objecten in de snaartheorie voorkomen: D-branen.
Afbeelding blokkenschema: Petr Kratochvil.