Voordat we het kunnen hebben over deze bijzondere oppervlakken, is het goed om even stil te staan bij wat een ‘oppervlak’ eigenlijk is. Misschien denk je bij dit woord aan het wateroppervlak of aan het oppervlak van de aardbol, of meer algemeen aan het buitenste of bovenste deel van iets. In de wiskunde zijn sommige oppervlakken inderdaad van deze vorm, maar wordt de term ‘oppervlak’ meer algemeen gebruikt voor alle vormen die, als je ver genoeg inzoomt, eruitzien als een plat vlak. Het aardoppervlak geeft een mooie illustratie van deze definitie: als je je op aarde bevindt, lijkt het net of het aardoppervlak plat is, maar in werkelijkheid is het grofweg de buitenkant van een bol, en dus in het bijzonder: gekromd. Of het oppervlak al dan niet de rand is van iets anders, zoals het aardoppervlak de rand is van de aarde, maakt wiskundig gezien niet uit: we zijn alleen geïnteresseerd in het tweedimensionale oppervlak zelf.
Een boloppervlak zoals ons aardoppervlak heeft een aantal fijne eigenschappen. Zo heeft het oppervlak geen rand: je kunt je in elke richting op het aardoppervlak bewegen, maar zult er (gelukkig) nooit vanaf vallen. Daarnaast is het een zogeheten oriënteerbaar oppervlak, wat betekent dat we op ieder punt een ‘oriëntatie’ kunnen definiëren op zo’n manier dat het consistent is over het hele oppervlak: op ieder punt kunnen we definiëren wat we bedoelen met ‘naar binnen’ en ‘naar buiten’. Concreet betekent dit dat, als je een rondje om de aarde zou reizen, er niets veranderd is als je weer terugkomt op de plek waar je begon. Je linkerhand zit nog steeds aan de linkerkant, en je staat ook niet ineens op z’n kop. Dat lijkt misschien heel vanzelfsprekend, maar we zullen snel zien dat dit niet voor alle oppervlakken geldt!
Een ander voorbeeld van een oppervlak dat wel ook deze eigenschappen bezit, is de torus: het oppervlak dat de buitenkant vormt van een donut. Hoewel de torus vaak wordt afgebeeld als het oppervlak van een driedimensionale donut, kunnen we hem ook tekenen als een soort bouwpakket in het platte vlak, namelijk als een rechthoek waarvan de overstaande zijden aan elkaar worden geplakt. Zo’n platte weergave is erg handig om meer ingewikkelde oppervlakken te kunnen bespreken. Voor de torus plakken we eerst twee tegenoverstaande zijden aan elkaar, zodat we een cilinder krijgen.
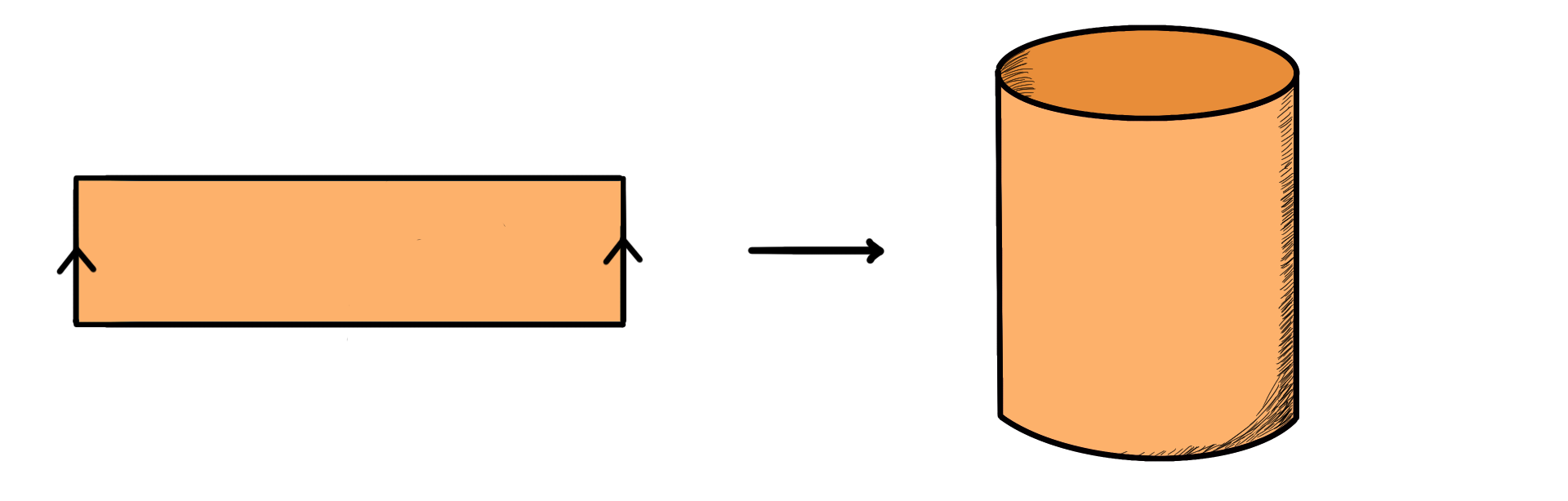
Als we nu de twee randen van de cilinder ook aan elkaar plakken, hebben we een torus.

Het boloppervlak, de torus en de cilinder zijn voorbeelden van oriënteerbare oppervlakken, maar zoals ik hierboven al liet doorschemeren bestaan er ook oppervlakken waarop we géén (consistente) oriëntatie kunnen definiëren. Het bekendste voorbeeld van zo’n niet-oriënteerbaar oppervlak is de Möbiusband, die in 1858 (onafhankelijk van elkaar) werd ontdekt door de Duitse wiskundigen Johann Bededict Listingen en August Ferdinand Möbius. Het bouwpakket van de Möbiusband lijkt erg op dat van de cilinder, maar nu plakken we de linker- en rechterzijde in tegenovergestelde richting aan elkaar – zie de afbeelding hieronder. In tegenstelling tot de cilinder heeft de Möbiusband maar één rand: als je met je vinger over de rand beweegt, kun je zonder je vinger op te tillen langs de hele rand gaan, en kom je dus ook langs de ‘overkant’ (Probeer dit gerust uit met een strook papier waarvan je de uiteindes aan elkaar plakt!) Daarnaast is het niet mogelijk om een consistente oriëntatie te definiëren op de Möbiusband: hoewel het lijkt alsof de band twee zijden heeft, is het niet mogelijk een ‘binnen-’ en ‘buitenkant’ aan te wijzen. Als je je vinger beweegt over wat je de ‘binnenkant’ zou willen noemen, kom je vanzelf ook langs de kant waarvan je dacht dat het de ‘buitenkant’ was. Een gevolg hiervan is ook dat je, als je één rondje over de Möbiusband zou lopen, als je spiegelbeeld terug zou komen bij het startpunt: op je kop, maar met ‘links’ en ‘rechts’ nog aan dezelfde kant! (Ook dit kun je eventueel zelf uitproberen door met een prikpen of naald poppetjes in een rondje over de Möbiusband te prikken.) Om ongespiegeld terug te komen op je startpunt, zou je twee rondjes over de Möbiusband moeten afleggen.

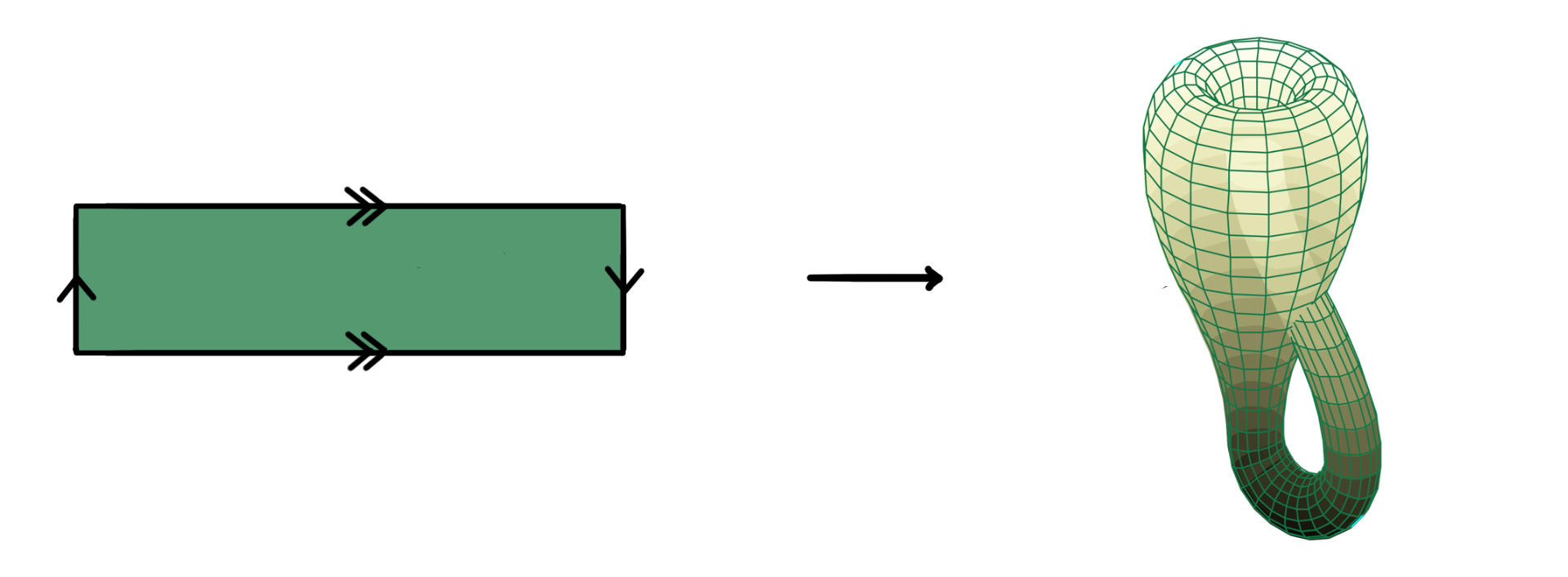
We kunnen een nog ingewikkelder oppervlak maken door het bouwpakket van de Möbiusband te nemen, en dan ook de boven- en onderkant in dezelfde richting aan elkaar te plakken, net als bij de torus. Het resultaat is de Kleinse fles, vernoemd naar de Duitse wiskundige Felix Klein. Als je de Kleinse fles probeert te maken van een strook papier, zul je er al snel achter komen dat dat niet lukt: de Kleinse fles kan niet worden gemaakt in onze driedimensionale wereld zonder zichzelf te doorsnijden. In een hypothetische vierdimensionale wereld zou dit wél mogelijk zijn. Net als de Möbiusband is de Kleinse fles niet-oriënteerbaar: de ogenschijnlijke ‘binnen-’ en ‘buitenkant’ gaan geleidelijk in elkaar over en vormen één doorlopend geheel. De Kleinse fles heeft bovendien geen rand.
Tot slot kunnen we ook de boven- en onderkant van ons bouwpakket in tegenovergestelde richting aan elkaar plakken, waardoor ieder punt op de rand aan zijn diagonaal tegenovergestelde punt wordt geplakt. Ook dit is niet mogelijk met een echte strook papier in onze driedimensionale wereld. Het wiskundige resultaat is een ander niet-oriënteerbaar en randloos oppervlak: het projectieve vlak.

Het nut van niet-oriënteerbare oppervlakken
Het moge duidelijk zijn dat er een scala aan wiskundige oppervlakken met bijzondere eigenschappen bestaat, maar wat is het nut van deze wiskundige constructies in de natuurkunde? Oriënteerbare oppervlakken, zoals het boloppervlak en de torus, duiken overal op in ons dagelijks leven, maar ook de Möbiusband heeft bepaalde praktische toepassingen. Zo werden in de vorige eeuw regelmatig lopende banden in de vorm van een Möbiusband gemaakt, omdat die gelijkmatig slijten over het hele oppervlak, en daardoor langer mee zouden gaan. Inmiddels wordt dit idee niet veel meer toegepast, omdat de twist van de Möbiusband ook voor spanning, en daardoor slijtage, zorgt, en de materialen waarvan lopende banden worden gemaakt zodanig zijn verbeterd dat de slijtage door wrijving veel minder is.
Een andere praktische toepassing is een elektrische weerstand in de vorm van een Möbiusband. Aan een gedetailleerde uitleg van deze weerstand kan een heel artikel worden gewijd, maar het resultaat is een weerstand met een lage zelfinductiecoëfficiënt. Met ‘zelfinductie’ wordt het verschijnsel bedoeld dat een object (zoals een weerstand of geleider) een verandering van elektrische stroom door dat object tegenwerkt. Wanneer de stroom die door een object loopt verandert, wordt een magnetisch veld opgewekt, en dit veld veroorzaakt een spanning die de verandering in stroom tegengaat. Hoe hoger de zelfinductiecoëfficiënt, hoe groter de spanning die wordt opgewekt, en hoe meer de stroomverandering wordt tegengewerkt. De Möbiusweerstand heeft een lage zelfinductiecoëfficiënt, wat dus betekent dat er weinig tegenwerkende spanning wordt geproduceerd, en veranderingen in stroom makkelijk worden toegelaten.
Ook in de wereld van metamaterialen – kunstmatig ontworpen structuren met bijzondere fysische eigenschappen – speelt niet-oriënteerbaarheid een verrassende rol. Zo heeft niet-oriënteerbaarheid een sterke invloed op de manier waarop een metamateriaal reageert op vervormingen, wat in de toekomst mogelijk gebruikt kan worden in robotica en voor quantumcomputers. In dit artikel lees je daar meer over.
In de theoretische natuurkunde duikt niet-oriënteerbaarheid op in de beschrijving van elementaire deeltjes, en in het bijzonder hun spin: een eigenschap waar je over na kunt denken als een soort impulsmoment (‘hoeveelheid draaiing’). Bosonen, zoals fotonen, hebben heeltallige spin (0, 1, 2, …), wat betekent dat ze na een rotatie over 360 graden weer terug zijn in hun begintoestand. Dit is in tegenstelling tot elektronen en andere fermionen, die halftallige spin (1/2, 3/2, 5/2, …) hebben: deze deeltjes moeten twee rondjes draaien (720 graden) voordat ze weer in hun begintoestand zijn. Deze tegenintuïtieve eigenschap wordt vaak uitgelegd aan de hand van de Möbiusstrip, want, zoals we gezien hebben, moeten ook daar twee rondjes worden afgelegd voordat we weer terug zijn in de begintoestand.
Niet-oriënteerbare oppervlakken en snaartheorie
Tot slot duiken niet-oriënteerbare oppervlakken op in mijn eigen onderzoek in quantumzwaartekracht en snaartheorie. Zoals in eerdere artikelen op deze website al beschreven, draait onderzoek naar quantumzwaartekracht erom een theorie te vinden die zwaartekracht in ons heelal (Einsteins relativiteitstheorie) en de natuurkunde op kleine schaal (de quantummechanica) met elkaar verenigt. Dat is verre van eenvoudig, dus wordt er veel onderzoek gedaan naar versimpelde modellen. Eén zo’n vereenvoudiging is om quantumzwaartekracht niet te bestuderen in de gebruikelijke vier dimensies (drie ruimtelijke dimensies en één tijddimensie), maar in minder dimensies. In het bijzonder wordt er onderzoek gedaan naar quantumzwaartekracht in twee dimensies: één ruimte- en één tijddimensie.
In dit vereenvoudigde tweedimensionale model neemt de ruimtetijd de vorm aan van een wiskundig oppervlak zoals ik die in dit artikel besproken heb. Zo’n oppervlak komt automatisch naar voren in de snaartheorie, waarin deeltjes niet als kleine puntjes, maar als trillingen van snaren worden beschreven. Als je het pad zou tekenen dat een lusvormige snaar aflegt in de ruimtetijd, vind je een vorm die eruitziet als een cilinder: de ene rand van de cilinder is waar de snaar begint, de andere rand is waar de snaar eindigt. Een van de vragen waar ik in mijn onderzoek naar kijk, is wat er gebeurt als we alle diagonaal tegenoverstaande punten van zo’n rand aan elkaar plakken, net als bij het projectieve vlak. Deze constructie wordt een crosscap genoemd, en verandert het pad van de snaar in een niet-oriënteerbaar oppervlak. Een motivatie om de crosscaps te bestuderen, is dat de uitkomsten van snaartheoretische berekeningen met die crosscaps in overeenstemming zijn met resultaten in tweedimensionale quantumzwaartekracht die via andere routes zijn gevonden. Over de fysische betekenis van het zo aan elkaar plakken van de ‘randen’ is echter nog veel onduidelijk; wie weet kom ik daar in de toekomst nog op terug!