
What if a tree out there on the street is actually not just the shape you see? As far as you know, that plant has many branches, leaves, roots — although most of them are deeply buried underground — and a trunk. If you cut off the bottom part of that trunk, then you will see the round cross section of the tree filled with multiple growth rings. In case you cut it on a bias, it will look more like an ellipse. In this way, the tree can look different in its cross sections. Now, let’s go in the other direction: what if there is some transcendental tree? Its shape — the branches, leaves, roots, and trunk — is just as familiar to you, but all of them together correspond to one single cross section of something even bigger. Does this sound feasible? Let me ask another, seemingly very different question: can you take out a ball from inside a closed box without opening it? These are not really absurd questions when it comes to dimensions.
The four-dimensional world

In Christopher Nolan’s 2014 film ‘Interstellar’, the main character Cooper swims around inside an object called tesseract. There, he observes his daughter’s bedroom from different angles. The exact scene will not be described here, to prevent any further spoilers in case you have not watched the film! Interested readers can refer to, for example, chapter 29 of the book ‘The Science of Interstellar’ by Kip Thorne. The book discusses what exactly happened to Cooper, the role of the tesseract in the movie, and also time which we will be ignorant of in this article. Instead, a question like ‘what is a tesseract?’ might have just popped into your head, and that we will discuss.
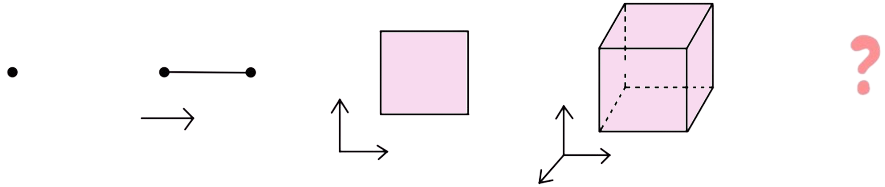
Let us pause for a second and first think about an object called a point. Mathematically, a point is considered a zero-dimensional object. Starting from there, you can allow the point to move in some direction or along an axis, as shown in figure 3. The trajectory of the point now forms a one-dimensional object, a line. Indeed, a line is considered to consist of infinitely many points. You might have started guessing what will come next; add one more direction perpendicular to the prior, move the line in that direction, and get a two-dimensional square. Moving the square in yet another perpendicular direction gives a three-dimensional cube. This is what you are familiar with in your everyday life; our universe is considered to be a four-dimensional world, including one time dimension and three spatial dimensions. Focusing on the spatial dimensions only, we humans are three-dimensional beings.
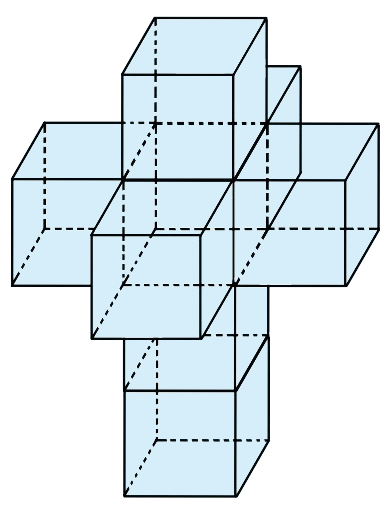
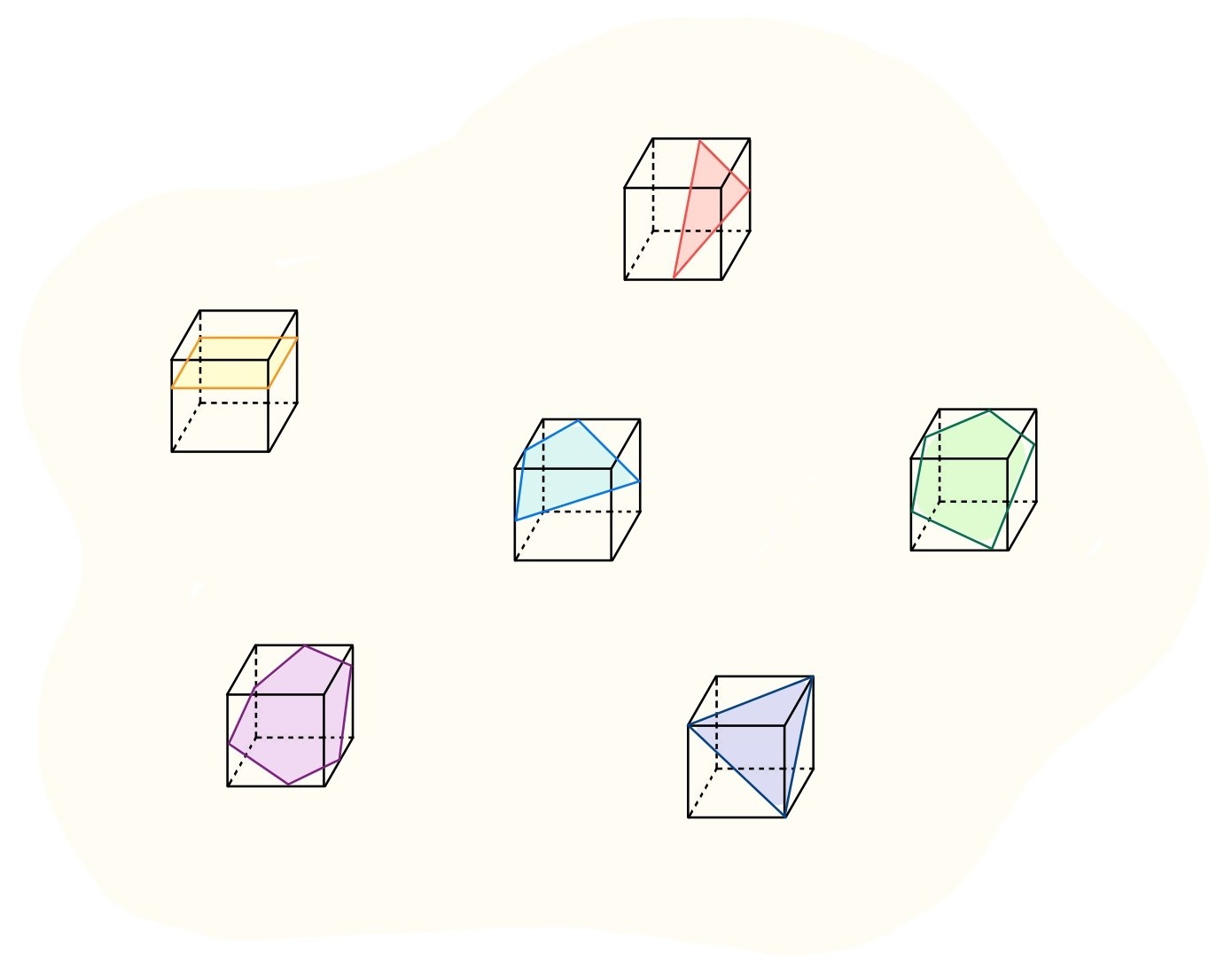
This is the right time to answer the question what a tesseract is. Following the logic we have developed above, another direction perpendicular to each of the three axes needed to describe a cube, let’s say: width, length, and height, can be introduced . The four-dimensional hypercube constructed in this way is called a tesseract. It is tremendously difficult to imagine the exact shape of a tesseract, for reasons that will be discussed later in this article. Instead, its so-called net, a ‘building instruction’ for the tesseract, is drawn in figure 4. As each side of a cube is a square, each side of a tesseract is a cube. The other way around, we can say that the cross sections of a tesseract are various different three-dimensional volumes just as those of a cube are two-dimensional polygons, see figure 5. Can you imagine what all those three-dimensional cross sections would look like? Or can you come up with a direction other than east-west, north-south, and up-down in the first place? Neither of those is easy, but now that we have built up the basic concept of dimensions, we can start considering what will happen to this world if there really exist some higher dimensional beings.
What if the entire world were different from what you perceive?
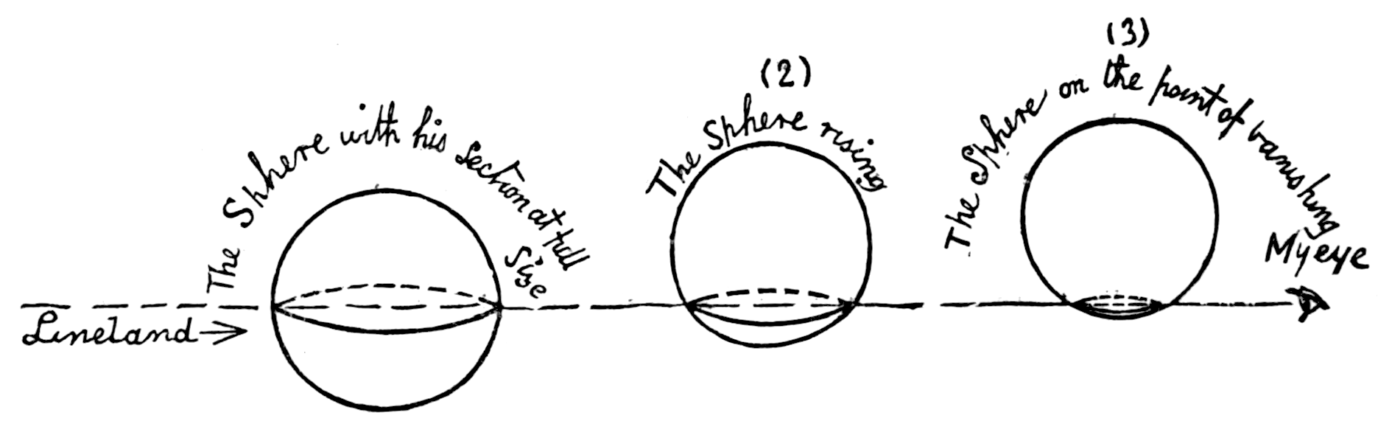
The animation ‘Flatland The Flim‘ (2007), based on the novel by Edwin A. Abbott published in 1884, intuitively explains the concept in the title above. In the film, a ‘Square’ living in Flatland travels to Lineland in a dream. Flying outside of Lineland, he soon recognizes that the line world consists of lines and also points, which may be thought of as cross sections of lines. However, the one-dimensional beings – Lines – living in Lineland do not see Square – until he actually enters their space they only hear his voice. Even after entering Lineland, the lines recognize the square only as a point, not as a two-dimensional plane. For them, the only spatial direction is just length. After waking up, Square comes back to his life in the flat plane world and meets ‘Sphere’, who only appears as a circle. Sphere freely changes its circumference and even disappears while moving in the third dimension outside Flatland. The space of a flat plane consists of length and width. The ‘circle’ tries to convince Square, who is in a state of panic, to understand the concept of one additional dimension, height. What will happen if Sphere meets someone from a four-dimensional world? He is a three-dimensional being just like us. Thus, the task of defining a 4D space will readily make him panic as much as Square from Flatland did.
Why is it difficult to imagine a four-dimensional space?
Now the question is: how can you see, feel, and distinguish a fourth dimension in space? It is tricky simply because we, as human beings, are confined to a three-dimensional space. The mechanism with which you can see an object is through the light which is emitted from the Sun, comes to the Earth, gets reflected on the object, and then is finally received by your eyes. The light passes through the eye lens and the image of the object is projected onto the retina. All these things, including the object of interest, eye lens, and retina are in three dimensions. Thus, even if the four-dimensional hypercube can be visualised as in the film ‘Interstellar’, the computer graphics, screens, and eventually the visualisation still remain those of a three-dimensional world. Maybe the situation is even worse, as the video is then projected on the 2D surface. So even if we are indeed embedded in a four-dimensional world, it is still tough to break the mold. Like Square, but one dimension higher, we will only be able to observe some 3D cross sections appearing from nowhere.
Apparently, our universe does not quite seem to be a cross section of a four- or higher dimensional space – at least, according to string theory. Instead, it might be a 3d membrane floating in a higher dimensional space called a bulk. Humans, trees, and other ordinary matters are confined to this membrane, but gravity is expected to travel through the bulk. The understanding of how the membrane or bulk behaves is outside the scope of this article. Still, if we can understand higher dimensions, what we see in our everyday lives such as a tree – if there exists a higher dimensional tree – might not be in the shape that we know!
What if we can play with higher dimensions?

Let us go back to the question asked in the very first part of this article: how can you take a ball out of a closed box? It seems quite challenging to even touch the ball without opening the box or using some magic tricks. Besides, it is not possible to see the ball unless the box is transparent. Being armed with the knowledge of dimensions, however, imagine drawing the whole system on a piece of paper. Now you can see a square and a circle in the plane. For a two-dimensional being this would seem like a square building and it would be impossible to see the circle in it. But if you are a three-dimensional being, you can look at it from above—from the third dimension—and simply lift the circle out of the building. The next step is to add one more dimension: remove a three-dimensional ball from a three-dimensional box, simply through a fourth dimension.
Already a long time ago, people made maps to see geographic features at a glance and easily find a route. Such a map is usually printed on the surface of a flat piece of paper. If you can freely play with dimensions, then you might also be able to make a map of a certain place printed on some volume of space. Then, you may again see the entire topography at a glance, just like you can see the system of a ball and a closed box drawn on a piece of paper. This way of thinking about more dimensions – whether they truly exist or not – will definitely allow us to find countlessly many routes to understand innumerous different things. What if teleportation technology could be realized in this way? What if we also consider the time dimension? In any case, the starting point is just a cross section.