
Van de klassieke wiskundige Archimedes wordt gezegd dat hij zijn meetkundige bewijzen met een stok in het zand tekende. Toen de Romeinen de stad Syracuse (op het huidige Sicilië) belegerden, schijnt Archimedes tegen een soldaat die zijn zandtekeningen kwam verpesten te hebben gesnauwd: ‘Noli turbare circulos meos!’, wat zoveel betekent als: laat mijn cirkels met rust! Een van de vraagstukken die Archimedes aan het Siciliaanse zand toevertrouwde was de volgende: stel je voor dat je een appel schilt, en neem voor het gemak aan dat de appel een perfecte bol is en dat je symmetrisch rond de as van de appel kunt schillen. Stel dat de straal van de appel \( R \) is en je een rond stuk schil afschilt met hoogte \( h \) , wat is dan het oppervlak van dat stukje schil? Zie in afbeelding 2 de geïdealiseerde appel en het stukje bolschil.
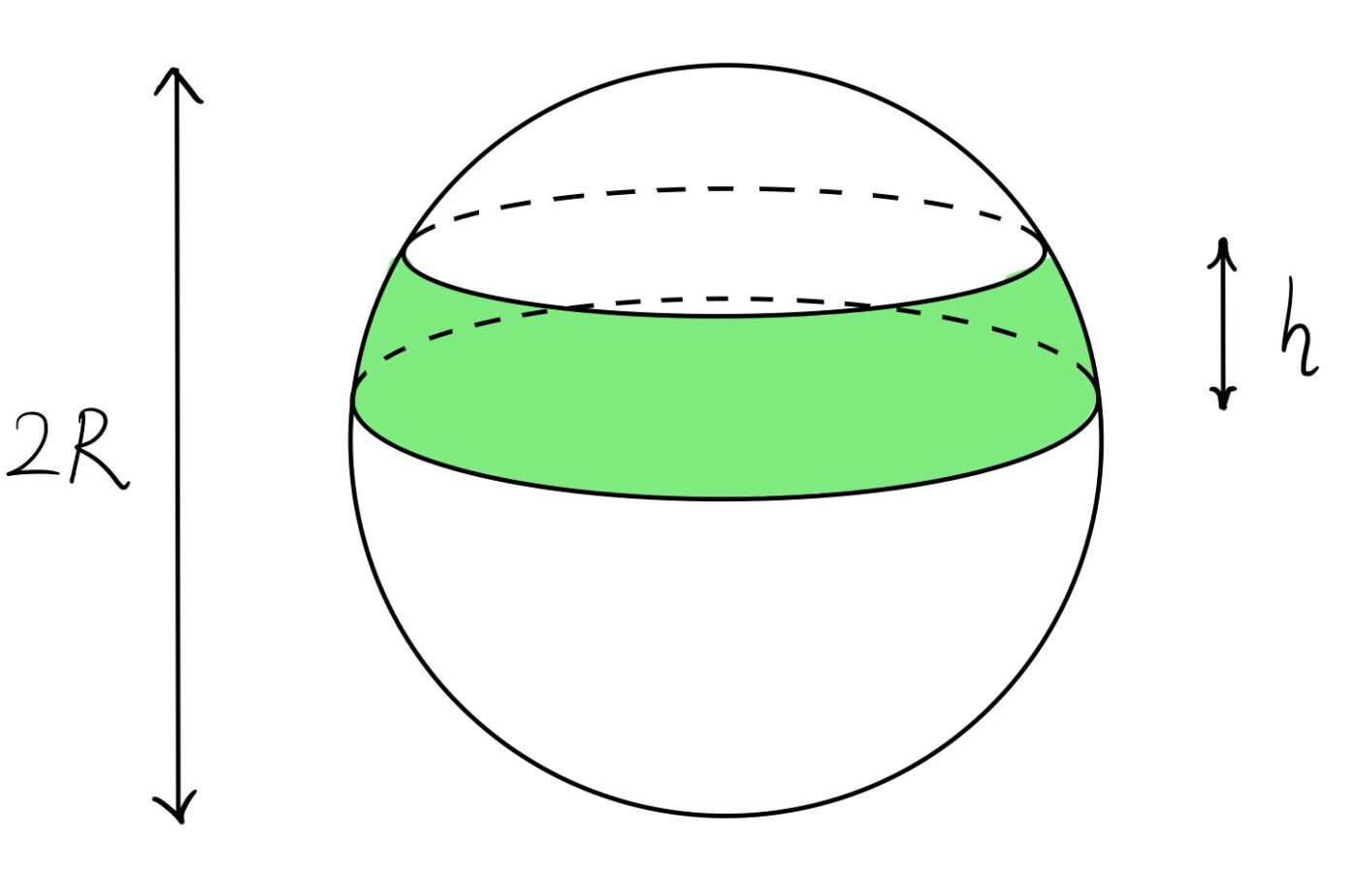
Archimedes bewees dat die oppervlakte gelijk is aan \( 2 \pi hR \) . Opmerkelijk genoeg hangt deze formule alleen af van de straal van de appel en de hoogte van het stukje schil, maar niet van waar op de appel je ’m afschilt: of je nu dicht bij de steel begint of ergens in het midden, het oppervlak van wat je afschilt is even groot (zolang je de hoogte \( h \) constant houdt). Er is een interessante balans die hiervoor zorgt: een schil van helemaal bovenop de appel heeft een kleinere straal, maar is tegelijkertijd sterker glooiend dan een schil rond het midden. Het wonderlijke is dat deze effecten elkaar precies opheffen wanneer we het oppervlak van een stukje schil berekenen1.
Minstens zo interessant is dat de formule \( A = 2\pi hR \) ook de formule is voor het oppervlak van een cilinder met straal \( R \) en hoogte \( h \) . En wanneer we voor \( h \) de hele hoogte van de appel invullen, namelijk \( h =2R \) , vinden we dat het oppervlak van een bol met straal \( R \) gelijk is aan \( 4\pi R^2 \) . Archimedes had daarmee bewezen dat het boloppervlak vier keer zo groot is als het oppervlak van de schaduw van diezelfde bol. Hij was zo gelukkig met deze factor 4 dat hij de formule op zijn graftombe liet graveren. Zo schrijft Cicero dat hij in 75 v.Chr., 137 jaar na de dood van Archimedes, diens grafsteen bekijkt en daar de afbeeldingen van een bol en een cilinder op ziet.
Maar wat heeft deze stelling met natuurkunde te maken? Daarvoor moeten we eerst 2000 jaar vooruitspoelen naar 1982, toen de Nederlandse wiskundigen Hans Duistermaat en Gert Heckman een stelling bewezen in de symplectische meetkunde, een deelgebied van de wiskunde dat geïnspireerd is op de klassieke mechanica van Hamilton. Deze stelling, die later naar hen vernoemd is, kun je zien als een veralgemenisering van de appelstelling van Archimedes. Dat zit zo: laten we de appelformule schrijven voor een infinitesimaal (dat wil zeggen: extreem klein) dun schilletje met hoogte \( \delta h \). Het oppervlak van dit schilletje is dus ook infinitesimaal groot, \( \delta A \). De appelformule zegt dan dat
\( \delta A = 2 \pi R \,\delta h \).
Dit kunnen we als volgt interpreteren: een kleine variatie van de hoogte resulteert in een kleine variatie van het oppervlak. De stelling van Duistermaat en Heckman is een veralgemenisering van dit resultaat van boloppervlakken naar een grotere klasse van vormen, de zogeheten ‘symplectische variëteiten’2. De veralgemenisering van de hoogtefunctie \( h \) heet een ‘momentafbeelding’, en de stelling zegt dat als je de momentafbeelding een beetje verandert, het oppervlakte-element \( dA \) evenredig meeverandert.
Lokalisatie op de vaste punten
Dit lijkt misschien een behoorlijk technisch resultaat, maar het blijkt verregaande implicaties te hebben in natuurkunde. De stelling van Duistermaat-Heckman heeft namelijk als gevolg dat bepaalde moeilijke integralen3 die we in de natuurkunde tegenkomen geëvalueerd kunnen worden door alleen de waarden te kennen op geïsoleerde punten, zogeheten ‘vaste punten’. We zeggen dan dat zo’n integraal ‘lokaliseert’ op de vaste punten. Om het fenomeen van lokalisatie een beetje beter te begrijpen, kijken we weer naar het voorbeeld van het boloppervlak (de appelschil) waarmee we dit artikel begonnen.
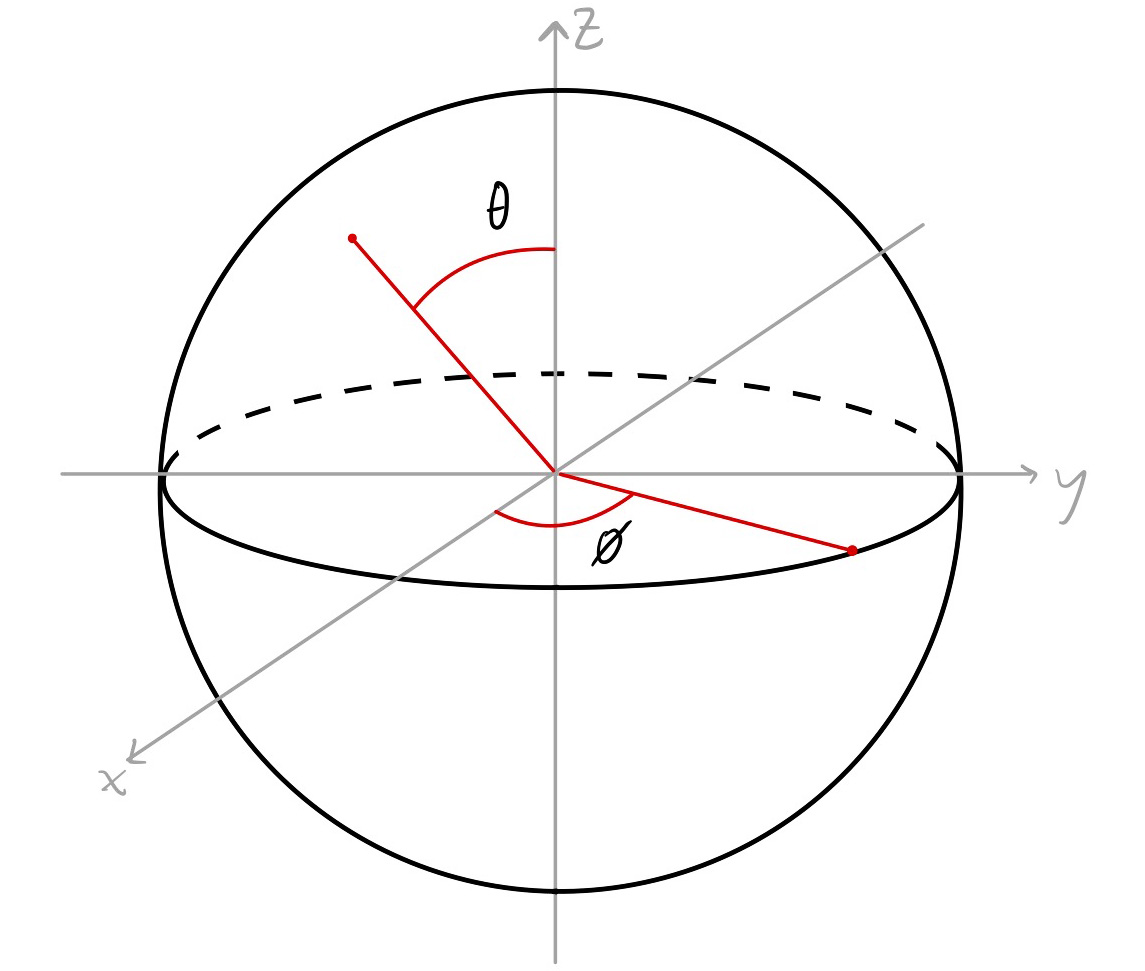
We beschrijven het tweedimensionale boloppervlak, dat we zullen aangeven met \( S^2 \), met twee hoeken: een ‘azimuthale’ hoek \( \phi \) die de rotaties om de \( z \)-as beschrijft, en een ‘polaire’ hoek \( \theta \) ten opzichte van die \( z \) -as, zie afbeelding 3. De hoogte \( h \) langs de \( z \) -as, gemeten vanaf de evenaar, kunnen we in termen van de hoek \( \theta \) uitdrukken als
\( h(\theta) = R\cos(\theta) \).
Stel dat we nu de volgende integraal over het boloppervlak willen uitrekenen:
\( I(\lambda) = \int_{S^2} e^{\lambda h} dA \).
waarbij \( \lambda \) een parameter is4. Natuurkundigen komen integralen zoals deze de hele dag tegen (daar komen we zo nog op terug). Meestal proberen we zulke integralen op te lossen door aan te nemen dat \( \lambda \) heel groot is en dan een benadering te maken in een reeks van machten van \( 1/\lambda \) (de zogeheten ‘methode van Laplace’)5. De belangrijkste bijdragen komen dan van de punten waar \( h(\theta) \) een maximum heeft, in dit geval op de noordpool van de bol \( (\theta = 0) \) , of waar \( h(\theta) \) juist een minimum heeft, hier op de zuidpool \( (\theta = \pi) \) . Een naïeve schatting van de integraal zou alleen de bijdragen op de noord- en zuidpool meenemen, terwijl betere benaderingen ook correcties die afhangen van \( 1/\lambda \) zouden meenemen.
Maar wat blijkt nu? In dit geval is het benaderen van de integraal door de waarde op de noord- en zuidpool niet slechts een benadering, maar het exacte antwoord. Oftewel: we hoeven helemaal niet de verdere reeks correcties die afhangen van \( 1/\lambda \) te berekenen, het antwoord is al exact ‘op eerste orde’, dus voor elke \( \lambda \) . We zeggen dat de integraal \( I(\lambda) \) gelokaliseerd is op de noord- en de zuidpool. De noord- en de zuidpool zijn de vaste punten waar ik zojuist over schreef: ze heten zo omdat het de enige punten op de sfeer zijn die op hun plaats blijven als je de sfeer om de \( z \)-as draait. Zulke rotaties om de \( z \)-as zijn een symmetrie van de integraal \( I(\lambda) \) , want de integrand (de uitdrukking die je integreert) hangt niet af van \( \phi \) . We zeggen dat de volledige symmetrie van de sfeer (álle mogelijke rotaties) wordt ‘gebroken’ tot de symmetrie van rotaties om alleen de \( z \) -as. De diepere onderliggende redenen dat de stelling van Duistermaat en Heckman geldt, zijn precies dit soort symmetrieën. Waar zouden we toch zijn zonder symmetrie!
Voor wie geïnteresseerd is in nog wat meer wiskunde (ben je dat niet, lees dan gerust door bij het volgende tussenkopje) kunnen we de integraal uit dit voorbeeld expliciet uitrekenen, om te bewijzen dat de enige bijdragen komen van \( h(0) \) en \( h(\pi) \) . Integreren op de sfeer doe je door voor het oppervlakte-element de volgende uitdrukking in te vullen: \( dA = d\phi \,d\theta \sin(\theta) \) , dus we moeten berekenen
\( I(\lambda) = \int_0^{2\pi} \int_0^\pi \sin(\theta) e^{\lambda R\cos(\theta)} d\theta d\phi \).
De integrand hangt niet af van \( \phi \) , dus de integraal over de hoek \( \phi \) geeft alleen een factor \( 2\pi \), de grootte van de cirkel. De integraal over \( \theta \) kunnen we uitrekenen door een substitutie te maken:
\( u = -\cos(\theta) \).
Als \( \theta \) van \( 0 \) tot \( \pi \) loopt, gaat \( u \) van \( -1 \) naar \( 1 \) . Aangezien we ook een uitdrukking in hoeken kunnen invullen voor \( du = \sin(\theta)d\theta \) , krijgen we
\( I(\lambda) = 2\pi \int_{-1}^1 e^{-\lambda R u} du = \frac{2\pi}{\lambda R} \left(e^{\lambda R} – e^{-\lambda R}\right) \).
Inderdaad zijn de termen tussen de haakjes precies de bijdragen van de noordpool \( e^{\lambda h(0)} \) en de zuidpool \( e^{\lambda h(\pi)} \)6.
Toepassingen in natuurkunde
Het soort integralen zoals we hierboven hebben bestudeerd is alomtegenwoordig in de natuurkunde. Zowel in de quantummechanica als in de quantumveldentheorie zijn integralen van deze vorm van groot belang (zie bijvoorbeeld het artikel over padintegralen). In dat geval is de parameter \( 1/\lambda \) bijvoorbeeld de constante van Planck, die we meestal met \( \hbar \) aangeven. Vaak zijn deze integralen onmogelijk om exact op te lossen, al bestaan er allerlei benaderingsmethodes. Maar wanneer een fysisch systeem ‘genoeg’ symmetrie heeft, kan het zo zijn dat de stelling van Duistermaat en Heckman van toepassing is: dan lokaliseert de integraal en vinden we wél een exact antwoord. Een van de eerste voorbeelden waarin dit het geval was, was Edward Witten’s oplossing van Yang-Millstheorie – een theorie voor krachten zoals de kernkrachten – in twee dimensies7. Een ander voorbeeld wordt gegeven door systemen met supersymmetrie: de lokalisatie van integralen zoals die in ons voorbeeld heet dan ‘supersymmetrische lokalisatie’. Ook het werk van de Iraanse mathematisch-fysicus Maryam Mirzakhani, waarmee zij als eerste vrouw de prestigieuze Fields-medaille won, steunde cruciaal op de gegeneraliseerde appelstelling van Duistermaat en Heckman. Mirzakhani’s werk uit 2007 heeft in de afgelopen jaren dan weer veel invloed gehad op het onderzoek waar ik me nu zelf mee bezig houd, namelijk aan ‘JT gravity’, een zwaartekrachtsmodel in twee dimensies. Zo zie je maar hoe een stelling die meer dan 2000 jaar geleden door Archimedes in het zand werd geschreven nog steeds in allerlei verschillende gedaantes opduikt en relevant blijft!
Bronnen
Voor de ‘appelstelling’ heb ik gebruikgemaakt van de afscheidsrede van Prof. dr. Gert Heckman. Meer over Archimedes is te vinden op de blog van John Baez.
[1] Probeer het zelf te bewijzen: zie deze pagina voor een hint.
[2] Een ander voorbeeld van een symplectische variëteit is de faseruimte, die in deze serie artikelen op QU wordt besproken.
[3] Een integraal is een oneindige optelsom, waarbij de dingen die je optelt steeds kleiner worden. Ken je het begrip integraal niet, dan kun je er hier meer over lezen.
[4] In het algemeen kan \( \lambda \) een complex getal zijn.
[5] Dit idee wordt verder uitgelegd in de serie artikelen over storingsrekening op deze site.
[6] Het relatieve minteken tussen de twee bijdragen komt doordat de noordpool een maximum is en de zuidpool een minimum van \( h(\theta) \).