Om deze vragen te beantwoorden moeten we eerst een duidelijk beeld krijgen van wat getallen eigenlijk zijn. Dit is wiskundig gezien een wat technischer onderwerp dan we in de meeste artikelen die op deze website verschijnen behandelen, maar laat dit je niet afschrikken! Om getallen uit te kunnen leggen, moet ik namelijk vertellen wat verschillende soorten getallen zijn. Dit valt onder de noemer ‘verzamelingenleer’, een puur wiskundig vakgebied dat begon met het werk van de wiskundige Georg Cantor in 1874, maar dat eigenlijk al in primitieve vorm door de oude Grieken werd bedreven.
Ruilhandel
Het eerste soort getallen zijn de natuurlijke getallen. Dit zijn waarschijnlijk ook de eerste getallen waar je aan denkt, en de getallen die in de oudheid als eerste werden gebruikt, bijvoorbeeld in de ruilhandel. Het zijn namelijk de getallen die je gebruikt om mee te tellen. Stel dat je een aantal broden hebt gebakken, dan kun je op je vingers tellen hoeveel broden je in totaal hebt: één, twee, drie, enzovoorts. De uitkomst is een natuurlijk getal, en al die natuurlijke getallen samen worden aangeduid als de verzameling
\( \mathbb{N}=\{1,2,3, \ldots \}. \)
Sommige wiskundigen rekenen het getal nul ook tot deze verzameling, maar de meningen verschillen over de vraag of dit wel of niet moet. Een wiskundige zal daarom, als hij of zij het over natuurlijke getallen heeft, altijd specificeren hierbij hoort of niet – en zoals je ziet vind ik van niet.
Het volgende soort getallen zijn de gehele getallen. Om terug te komen op het voorbeeld van ruilhandel: na het bakken van de broden kan je afspreken met een vriend om één brood te ruilen voor vier appels. Als die vriend op dat moment maar twee appels heeft, kan hij voorstellen om alsnog te ruilen en te beloven om die overige twee appels later te geven. Hij staat dan bij je in het krijt en is je twee appels schuldig. Effectief heeft hij op dat moment dus minus twee appels – een negatief aantal. De gehele getallen zijn de natuurlijke getallen samen met alle negatieve getallen en nul, aangeduid als de verzameling
\( \mathbb{Z}=\{\ldots ,-2,-1,0,1,2, \ldots \}. \)
Er is een andere manier om de gehele getallen te definiëren, namelijk als een paar van twee natuurlijke getallen. Dit is door Marcel Vonk al eens beschreven in zijn serie over K-theorie, maar ik zal het argument kort herhalen. In het voorbeeld over broden en appels, heeft onze vriend maar twee appels, waar hij er eigenlijk vier nodig had. We schrijven deze getallen als het paar \( (2,4) \), zo zien we dat de vriend twee appels tekort heeft, namelijk \( 2-4=-2 \). Stel nu dat hij niet één brood, maar twee broden wilde kopen, maar dat hij zes appels had in plaats van de benodigde acht appels. Dan zou hij óók twee appels tekortkomen. Het eindresultaat voor het paar \( (6,8) \) is hetzelfde als voor \( (2,4) \), en inderdaad weten we dat \( 6-8=2-4=-2 \).
We kunnen negatieve getallen dus opschrijven als paren van positieve getallen, maar moeten daarbij voorzichtig zijn omdat sommige paren hetzelfde negatieve getal beschrijven. Om aan de hand van zulke paren de negatieve getallen te definiëren, moeten we de paren met gelijke uitkomst groeperen. Zo’n groepering heet in de wiskunde een equivalentieklasse. In dit geval, voor paren van natuurlijke getallen \( (a,b) \) en \( (c,d) \), moet gelden dat \( a-b=c-d \) om ze hetzelfde getal te laten beschrijven. Oftewel, als we dit omschrijven zodat de mintekens verdwijnen, zitten deze twee paren in dezelfde equivalentieklasse als
\( a+d=c+b. \)
Dit is de algemene eis die we stellen voor alle paren van natuurlijke getallen, en zo hebben we een nette definitie van de gehele getallen.
Breken van het brood
Als je je vriend misschien wat minder vertrouwt, of als er een onbekende is die met maar twee appels aan komt zetten, wil je niet dat hij twee appels aan je verschuldigd is. Om hem dan toch tegemoet te komen, kan je aanbieden om het brood doormidden te breken en één van de twee delen te ruilen voor twee appels. We noemen zo’n deel van een brood natuurlijk een half brood, wat we kunnen opschrijven als een breuk: \( \frac{1}{2} \). Je had het brood ook in vieren kunnen breken: één deel voor elke appel. Dan had je vriend twee van zulke delen kunnen meenemen, oftewel \( \frac{2}{4} \) brood. Het resultaat is natuurlijk hetzelfde.
Zulke delen van gehele getallen noemen we breuken. Misschien zie je al waar dit heen gaat: we kunnen een breuk aangeven als een paar gehele getallen \( (a,b) \), met \( b \) ongelijk aan nul. Twee van zulke paren \( (a,b) \) en \( (c,d) \) definiëren dan dezelfde breuk als
\( \frac{a}{b} = \frac{c}{d} \)
wat we zonder delingen te gebruiken ook kunnen schrijven als
\( ad=bc. \)
De verzameling paren die dezelfde breuk definiëren, stoppen we weer samen in een equivalentieklasse. De verzameling van alle equivalentieklassen van deze soort bij elkaar, oftewel van alle breuken, wordt door wiskundigen de verzameling van rationale getallen genoemd en aangeduid met \( \mathbb{Q} \).
In de tijd van de oude Grieken waren de meningen over of er méér was dan alleen de rationale getallen verdeeld. Zoals al eerder geschreven op deze website, gaat het verhaal dat de Griek Hippasus uit de groep van Pythagoras bewees dat de wortel van twee níét rationaal is, wat de rest van de groep van Pythagoras zó tegenstond dat ze Hippasus hebben verdronken. Toch had Hippasus gelijk…
Maar voor we terugkomen op het lot van Hippasus, moeten we eerst iets zeggen over het aantal rationale getallen. Op het eerste gezicht lijkt het namelijk alsof er véél meer rationale getallen zijn dan natuurlijke getallen, het is immers zo dat élk natuurlijk getal óók een rationaal getal is. Toch zijn er precies even veel rationale getallen als natuurlijke getallen! Hoeveel dat er zijn hebben wiskundigen een naam gegeven: dat zijn er namelijk aftelbaar oneindig veel. Maar hoe is het mogelijk dat beide verzamelingen “even groot” zijn, en wat bedoelen we eigenlijk als we zeggen dat twee oneindig grote verzamelingen even groot zijn? Dat is het makkelijkste om in te zien aan de hand van een afbeelding.
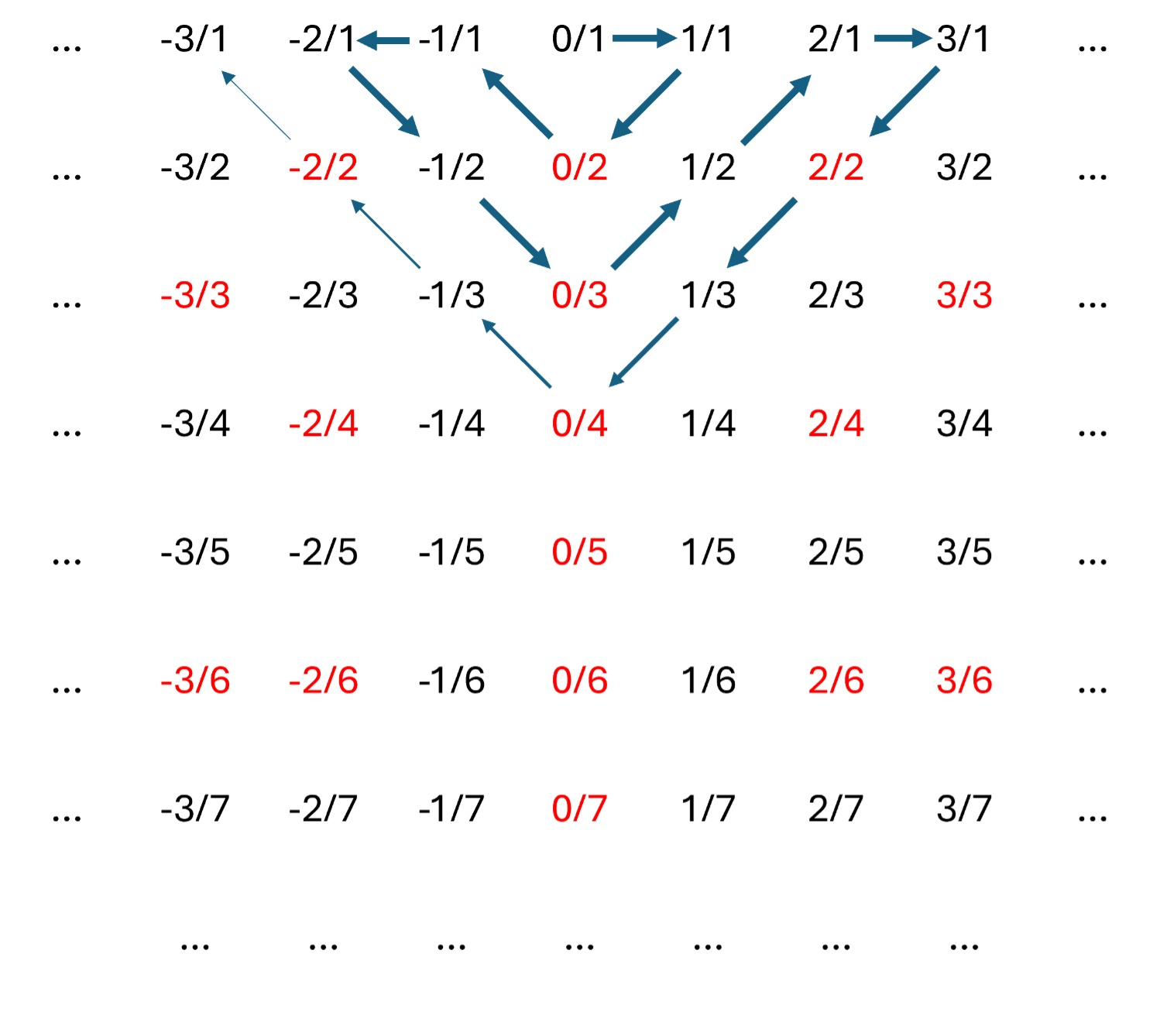
We zien in de afbeelding dat alle rationale getallen in een rooster zijn gezet. In het rooster zijn blauwe pijlen getekend, die beginnen bij \( \frac{0}{1} \), vervolgens naar \( \frac{1}{1} \) gaan, dan naar \( \frac{0}{2} \), enzovoorts, kronkelend door het rooster. Op deze manier komen we elk rationaal getal tegen, en door bij dit proces de rationale getallen af te tellen kennen we aan elk natuurlijk getal een rationaal getal toe, afhankelijk van de positie van het rationale getal op de kronkelende lijn. Als we toevallig een getal tegenkomen wat we al eerder hebben gezien, zoals bij \( \frac{0}{1} \) en \( \frac{0}{2} \), laten we dit getal weg uit de lijn. Zo correspondeert elk natuurlijk getal precies één op één met een rationaal getal: één wordt gekoppeld aan nul, twee wordt gekoppeld aan één, drie wordt gekoppeld aan minus één, enzovoorts. Als er méér rationale getallen zouden zijn dan natuurlijke getallen, had er wel ten minste eentje moeten zijn waarvoor we géén partner zouden kunnen vinden. We zien dat dit niet het geval is, dus er zijn net zoveel rationale getallen als natuurlijke getallen!
Tussen de kruimels
Het was voor Hippasus niet eens zo moeilijk om te bewijzen dat de wortel van twee niet rationaal (oftewel, irrationaal) is. Ik zal laten zien hoe. De makkelijkste techniek voor het bewijs, is een bewijs uit het ongerijmde: neem aan dat het tegenovergestelde waar is en laat zien dat dit tot een tegenspraak leidt. We nemen dus aan dat \(\sqrt{2}=\frac{a}{b}\), en voor het gemak kiezen we de gehele getallen \(a\) en \(b\) zo klein mogelijk. (Vraag: waarom kan dat?) Kwadrateer nu beide kanten; door vervolgens links en rechts te vermenigvuldigen met \(b^2\), zien we dan dat \(2b^2=a^2\). Maar dat betekent dat \(a^2\) even is en dus dat \(a\) zélf even is. (Vraag: waarom is dat zo?) Daaruit volgt vervolgens dat óók \(b^2\) even is. (Ga dit na.) Maar dan konden we zowel \(a\) als \(b\) door twee delen zonder de breuk \(\frac{a}{b}\) te veranderen, en waren \(a\) en \(b\) dus niet zo klein mogelijk: een tegenspraak! Dus de wortel van twee kunnen we niet als breuk schrijven: het getal moet wel irrationaal zijn.
Hiermee zit de wortel van twee als het ware ‘tussen de rationale getallen in’. Andere voorbeelden van dit soort getallen zijn \( \pi \) en het eulergetal \( e \), vernoemd naar de wiskundige Leonhard Euler. Voor deze twee getallen is het moeilijker om te bewijzen dat ze niet rationaal zijn. De rationale getallen samen met de getallen die hier ’tussenin’ zitten (waarvan ik nog moet vertellen welke dat precies zijn), heten de reële getallen, een verzameling die wiskundigen aangeven met \( \mathbb{R} \). De wiskundige Norman Wildberger noemt deze naamgeving (vrij vertaald) “een vlaag van genialiteit waar elk PR-persoon trots op zou zijn”[1]. Dit schreef Wildberger omdat ironisch genoeg kan worden beargumenteerd dat het grootste deel van de ‘reële’ getallen helemaal niet opgeschreven kan worden, dus is er weinig ‘reëel’ aan zo’n getal. Op de reden dat we de reële getallen niet allemaal kunnen opschrijven, en wat maakt dat je kan beargumenteren dat veel reële getallen niet fysisch zijn, kom ik later terug. Eerst moet ik beter uitleggen wat ‘tussen de rationale getallen inzitten’ betekent.
Er zijn verschillende definities van de reële getallen, die op hetzelfde neerkomen. Het meest inzichtelijk vind ik een constructie van de getallen aan de hand van rijtjes die snel genoeg convergeren naar een getal. Intuïtief heb je al een heel goed idee van wat reële getallen zijn: het zijn getallen met een oneindig lange decimale expansie. Bijvoorbeeld \( 1=1{,}00000\ldots \), waar de drie puntjes ervoor staan dat cijfers achter de komma oneindig lang door blijven gaan (in dit geval altijd als nullen). Een ander voorbeeld is weer de wortel van twee, waarvan de decimale expansie als volgt begint:
\( \sqrt{2}=1{,}414213562\ldots, \)
Weer betekenen de drie puntjes dat de cijfers achter de komma oneindig lang doorgaan, maar dit keer zit er geen herhalend patroon in de verdere cijfers. In het geval van de wortel van twee zien we dat we steeds dichter bij de échte waarde kunnen komen door steeds één decimaal meer te nemen: het rijtje \( 1, 1{,}4, 1{,}41, 1{,}414, 1{,}4142, 1{,}41421, \ldots \) komt stapje voor stapje dichterbij. Wat je misschien ook opvalt is dat élk van de getallen in dit rijtje een rationaal getal is, we kunnen bijvoorbeeld \( 1{,}414 \) schrijven als \( 1{,}414=\frac{1414}{1000} \). Aan de hand van een zelfde soort rijtje dat we vinden door de decimale expansie van een willekeurig reëel getal, zien we dat dit altijd het geval is: er bestaat een rijtje van rationale getallen dat convergeert naar het reële getal in kwestie.
Wiskundigen noemen zo’n rijtje een cauchyrij, vernoemd naar de wiskundige Augustin-Louis Cauchy. De formele wiskundige definitie is als volgt: een rijtje getallen \( a_1, a_2, a_3, \ldots \) is Cauchy als er voor elk positief rationaal getal \( \epsilon>0 \) een natuurlijk getal \( N\in\mathbb{N} \) bestaat, zodat voor elke \( n,m>N \), het verschil \( |a_n-a_m|<\epsilon \) is. Dit is een hele mond vol, en als je dit voor het eerst ziet moet je het wellicht een paar keer lezen, maar het is een goede oefening om te bekijken of deze definitie inderdaad geldt voor het rijtje dat we opschreven voor de wortel van twee. Het belangrijkste aan een cauchyrij is dat de verschillen tussen de getallen steeds verder in het rijtje steeds kleiner worden.
Er is echter nog een kleine voorzichtigheid geboden. Bijvoorbeeld het getal \(0{,}99999\ldots \), waar achter de komma alléén negens staan, is gelijk aan het getal 1. Dit is redelijk snel in te zien door de decimale expansie van \( \frac{1}{3} \) op te schrijven en te gebruiken dat \( 3\cdot\frac{1}{3}=1 \). Het is daarom beter om de reële getallen te definiëren als de bijbehorende cauchyrijtjes zélf in plaats van als de limiet van zo’n rijtje, en vervolgens (net als voor de gehele en rationale getallen) een equivalentieklasse van cauchyrijtjes te definiëren, waarbij we zeggen dat twee cauchyrijtjes gelijk zijn als het verschil tussen de twee rijtjes naar nul gaat. Dat wil zeggen, als \( b_1, b_2, b_3, \ldots \) ook een cauchyrij is, is deze equivalent aan het eerdere rijtje als \( a_n-b_n \) naar nul gaat zodra \( n \) groter wordt.
Méér dan telbaar
Het moge duidelijk zijn dat het definiëren van de reële getallen wat meer werk was dan het definiëren van gehele getallen of rationale getallen. In plaats van equivalentieklassen van twee natuurlijke of twee gehele getallen, hebben we nu equivalentieklassen van snel genoeg convergerende rijtjes rationale getallen nodig. Iets wat ons zo natuurlijk voorkomt als de reële getallen, heeft daarmee een heel onnatuurlijke wiskundige definitie. Maar de echte schok kwam toen de wiskundige Georg Cantor in 1874 bewees dat er méér reële getallen zijn dan dat er natuurlijke getallen zijn: het zijn er of overaftelbaar veel.
In 1891 bewees Cantor dit nogmaals, gebruikmakend van een prachtig argument, wat het diagonaalargument van Cantor wordt genoemd. Laten we dit argument bekijken, waarbij we ons voor het gemak concentreren op alleen de getallen tussen nul en één. Ook dit bewijs is een bewijs uit het ongerijmde: stel dus dat de getallen tussen nul en één wél telbaar zijn. Dan kunnen we aan elk natuurlijk getal precies één getal tussen nul en één koppelen. Dit kunnen we weergeven in een lijst, die oneindig lang doorgaat, zoals weergeven in onderstaande afbeelding. Deze lijst bevat, volgens onze aanname, álle getallen tussen nul en één. Als het ons dus lukt om een getal te vinden dat níét in de lijst voorkomt, maar wel tussen nul en één zit, hebben we een tegenspraak gevonden en concluderen we dat de reële getallen niet telbaar zijn. Laten we zo’n getal construeren.
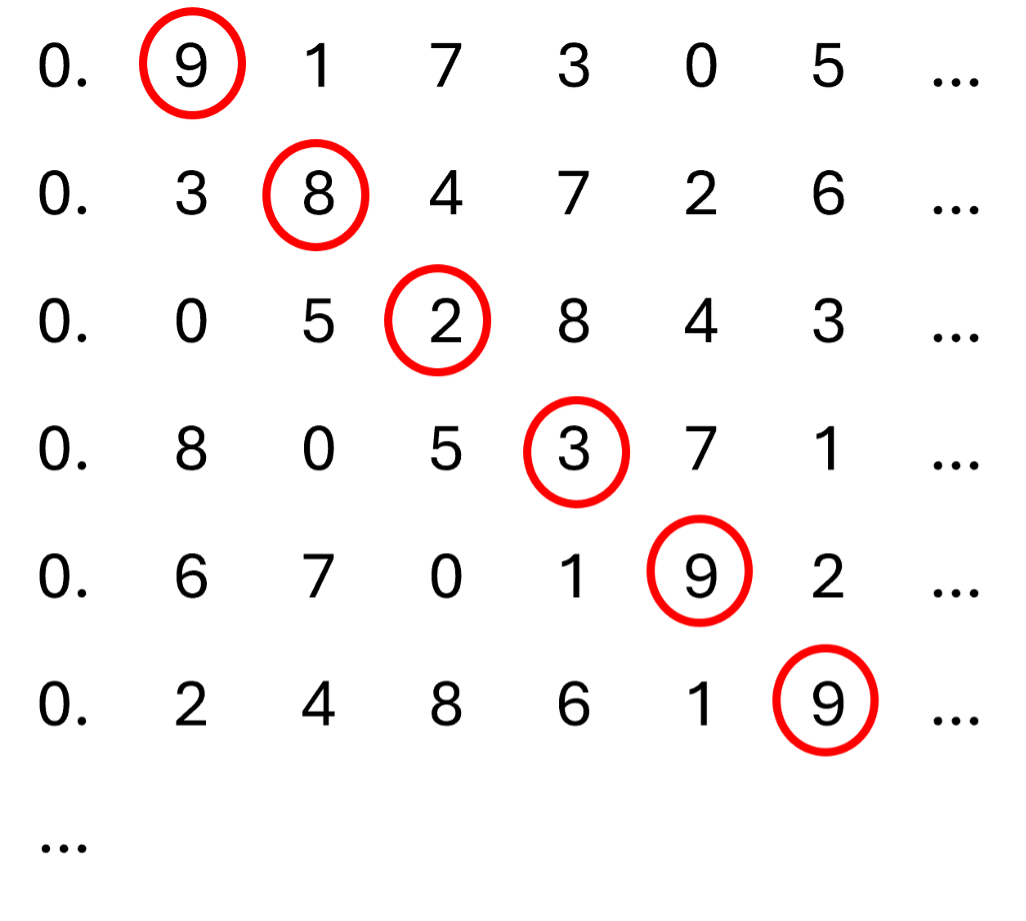
Voor de constructie van het nieuwe getal kijken we naar het eerste getal in de lijst, en nemen we de eerste plek in de decimale expansie van dit getal. Als dit een drie is, krijgt ons nieuwe getal op de eerste decimale plek een vier, zo niet, dan krijgt ons nieuwe getal op de eerste decimale plek een drie. (De cijfers ‘drie’ en ‘vier’ heb ik hier willekeurig gekozen; je kunt dezelfde truc ook met bijvoorbeeld ‘vijf’ en ‘zes’ uithalen.) In het voorbeeld in de afbeelding zien we in het eerste getal in de lijst een negen op de eerste decimale plek, wat betekent dat het nieuwe getal een drie krijgt op die plek. Vervolgens gaan we naar het tweede getal in de lijst en kijken we naar de tweede decimale positie van dit getal. Als op die positie een drie staat, krijgt ons nieuwe getal een vier, anders een drie. In het voorbeeld verandert de acht daarom in een drie. Zo gaan we elk getal in de lijst af om ons nieuwe getal op te schrijven. Wat we zien is dat dit nieuwe getal anders is van het eerste getal in de lijst, omdat het op de eerste decimale plek verschilt. Ook is het anders van het tweede getal in de lijst, omdat het op de tweede decimale plek verschilt. In het algemeen: het nieuwe getal is anders dan het \( n \)-de getal in de lijst omdat het verschilt op de \( n \)-de decimale plek. Zo hebben we een getal gemaakt tussen nul en één dat niet in de lijst voorkomt. Dit is een tegenspraak met onze aanname dat élk getal tussen nul en één in de lijst zou staan, dus de reële getallen zijn niet telbaar![2]
Sinds het werk van Cantor is het duidelijk geworden dat er niet één soort oneindigheid is, maar meerdere soorten. Zo bleek het dat er ook oneindigheden zijn die nog groter zijn dan de oneindigheid van de reële getallen. Hier zal ik verder niet op in gaan; wat we graag willen zien is hoe de grote hoeveelheid van reële getallen zelf al belangrijk, of problematisch, is voor de natuurkunde.
Echte getallen
De grote hoeveelheid reële getallen leidt tot een verrassende conclusie, die – zo vond ik tenminste – de eerste keer dat je haar hoort een beetje flauw klinkt. Met behulp van de definitie hierboven weten we dat de reële getallen precies de equivalentieklassen van cauchyrijtjes bestaand uit rationale getallen zijn. Maar, om dan een willekeurig reëel getal op te schrijven hebben we tenminste één zo’n cauchyrijtje in de equivalentieklasse in z’n geheel nodig. Dat wil zeggen: om één reëel getal op te schrijven hebben we een rijtje met (aftelbaar) oneindig veel termen nodig. Voor de rationale getallen zelf is dat niet zo moeilijk, bijvoorbeeld het getal \( \frac{1}{2} \) wordt gedefinieerd door de constante cauchyrij \( \left(\frac{1}{2},\frac{1}{2},\frac{1}{2},…\right) \). Maar voor andere getallen wordt het lastiger om élke term van een bijbehorende cauchyrij precies te weten; het rijtje voor de wortel van twee dat we eerder zagen kunnen we met behulp van de computer een heel eind uitrekenen, maar om achter álle decimale posities te komen is onmogelijk.
Om toch precies te vertellen wat de wortel van twee is, kunnen we een andere truc gebruiken: we zeggen: ‘De wortel van twee is de positieve oplossing van de vergelijking \( x^2=2 \).’ In deze vergelijking komen alleen rationale getallen voor (in dit geval zelfs alleen gehele getallen), dus voor deze vergelijking zelf lopen we niet tegen het probleem dat we álle termen van een cauchyrij nodig hebben, maar niet weten. Een vergelijking waarbij wel alle termen van een cauchyrij nodig zijn, is bijvoorbeeld \( x-a=0 \) met een irrationaal getal \( a \). Voor zo’n vergelijking werkt daarom ‘de wortel-twee-truc’ niet. Iets soortgelijks kunnen we doen voor \( \pi \), dan zeggen we namelijk: ‘Het getal \( \pi \) is de helft van de omtrek van een cirkel met straal één.’ En, nog een iets lastiger voorbeeld voor het eulergetal: ‘Het eulergetal \( e \) is waarvoor geldt dat de afgeleide van de functie \( f(x)=e^x \) gelijk is aan zichzelf.’[3]
Deze drie manieren om een reëel getal op te schrijven hebben één ding gemeen: het is met een eindig aantal woorden – of om nauwkeuriger te zijn: met een eindig aantal tekens – precies duidelijk welk getal we bedoelen. Het klinkt vanaf daar niet eens als een gek idee om een nieuw soort getal te definiëren, laten we zeggen: een echt getal, wat een getal is dat we in een eindig aantal tekens ondubbelzinnig kunnen aanduiden. Maar nu komt de verrassing: elke taal heeft slechts een eindig aantal tekens, wat betekent dat er maar aftelbaar veel mogelijkheden zijn om die tekens te combineren tot een eindige hoeveelheid. Dus, onafhankelijk van de taal die we gebruiken (in dit geval Nederlands gemengd met wiskunde), zijn er maar telbaar veel ‘echte getallen’! Dit betekent dat er (een heleboel!) reële getallen níét ‘echt’ zijn. Dat verklaart meteen waarom de naamgeving van de ‘reële’ getallen zo’n waanzinnig goede PR-stunt was, want wat is er reëel aan een getal dat we niet kunnen, en ook nooit zullen kunnen, opschrijven?
Quantummechanica en informatie
Na al mijn gebrabbel over verschillende soorten getallen en verschillende soorten oneindigheden is het, neem ik aan, nog volstrekt onduidelijk wat dit met natuurkunde te maken heeft. Dit wordt duidelijk als we het kort hebben over twee zaken die vaak op deze website genoemd worden: quantummechanica en informatie.
Ten eerste de quantummechanica. Aan het begin van de ontwikkeling van de quantummechanica was het duidelijk dat bepaalde verschijnselen in de natuur niet continu zijn, maar juist discreet. In het bijzonder doel ik dan op spectraallijnen van een atoom, die al vaak besproken zijn, zoals recent in mijn eerdere artikel. De quantummechanica weet dit discrete gedrag uitstekend te beschrijven.
Ten tweede informatie. De interesse van natuurkundigen in informatie is voortgevloeid uit de quantummechanica. Een gedetailleerde beschrijving van deze ontwikkelingen door de geschiedenis heen zal ik niet geven, maar als je meer wil weten is er een hoop te lezen in de serie snaren en holografie van Marcel Vonk. De conclusie die wij nodig hebben, is dat er in een bepaald volume in de ruimte maar een maximale hoeveelheid informatie past, namelijk precies zoveel als de informatie van een zwart gat .

Als we de informatie weergeven in termen van bits, vormen die bits een taal. Deze taal kan worden gebruikt om echte getallen mee aan te duiden. Om een getal, in wat voor vorm dan ook, in de natuur tegen te komen, moet het zich bevinden in een eindig volume. In zo’n volume passen maar eindig veel bits, waarmee een eindige combinatie van tekens gemaakt kan worden. Dus, als we nu terugdenken aan onze discussie van zojuist, betekent dit dat we niet élk reëel getal in de natuur kunnen aantreffen! Er zijn een heleboel reële getallen die niet kunnen worden opgeschreven aan de hand van de bits van informatie. Zo hebben we beargumenteerd dat er maar aftelbaar veel getallen in het heelal kunnen voorkomen, en daarmee fysische getallen zijn. We zouden die getallen misschien ‘natuurlijke getallen’ willen noemen, maar die naam is helaas al bezet. Zo is de naam ‘echte’ getallen misschien ook niet optimaal, omdat ‘echt’ wel heel erg lijkt op ‘reëel’.
Een probleem? Een oplossing?
Je vraagt je nu misschien af of het een probleem is dat veel van de wis- en natuurkunde gebaseerd is op de reële getallen, waarvan een groot deel niet eens in de natuur voorkomt. Er zijn inderdaad natuurkundigen en wiskundigen die kritisch zijn over het gebruik van de reële getallen. Een voorbeeld van zo’n natuurkundige is de Roger Penrose, die hierover schreef in zijn boek ‘The road to reality’. Een voorbeeld van zo’n wiskundige is de Nederlander Eric Opdam, die zijn twijfels heeft over hoe het begrip ‘existentie’ wordt gebruikt in de wiskunde, en daarvoor een striktere definitie aanhoudt dan de meeste wiskundigen. Dat maakt ook dat hij wiskundige constructies op basis van de reële getallen minder ‘vertrouwt’[4].
Toch valt het niet te betwisten dat de reële getallen ook heel nuttig zijn. Een heel groot deel van onze technologie is mede mogelijk gemaakt door reële getallen: met behulp van analyse kunnen we differentiaalvergelijkingen opstellen, waarmee bijvoorbeeld de stevigheid van bruggen en gebouwen wordt bepaald, of waarmee het weer wordt voorspeld. Met behulp van algemene relativiteit kunnen uitstekende voorspellingen over het heelal worden gedaan, en hierdoor bestaat het GPS-systeem. In al die constructies zijn de reële getallen essentieel. Ook de quantummechanica is gebaseerd op (ten minste) de reële getallen.
De reële getallen hebben ons als mensheid dus een hoop kennis gebracht. Maar wat er, vanuit het oogpunt van een theoretisch natuurkundige, nog mist, is een theorie van quantumzwaartekracht. Wellicht is het voor zo’n theorie – waarvan veel natuurkundigen vermoeden dat informatie er een centrale rol in speelt – nodig om alleen de ‘echte’ getallen te gebruiken. In elk geval weten we nu dat niet álle reële getallen in de natuur, en daarmee in een zo eenvoudig mogelijke alomvattende theorie van de natuur, voor kunnen komen. Om de quantumzwaartekracht als een nette wiskundige theorie op te schrijven, zal het dan – helaas – misschien wel nodig zijn om een hoop wiskunde opnieuw uit te vinden met behulp van ‘echte’ getallen, of om op een of andere manier de reële getallen te omzeilen.
De wiskunde opnieuw uitvinden lijkt een monsterklus, zeker omdat het nu nog helemaal niet duidelijk is wat precies alle echte getallen zijn, die met behulp van onze taal opgeschreven kunnen worden, laat staan in de taal van het heelal. Om dit artikel af te sluiten, zal ik nog benoemen wat we in ieder geval kunnen verwachten. Wat ik natuurlijk hierboven al had benoemd, waren de rationale getallen zelf; die kunnen we rekenen tot de echte getallen. Verder had ik het al over de wortel van twee, die we kunnen aanduiden als de oplossing van \( x^2-2=0 \). Dit idee kunnen we uitbreiden, door te zeggen dat van een willekeurige polynomiale vergelijking \( p(x)=0 \), met \( p(x)=a_0 +a_1 x^1 +… + a_n x^n \) en alle \( a_i \) rationaal, echt zijn. Dit geeft de zogeheten algebraïsche getallen. Er zijn algebraïsche getallen die zelf niet reëel zijn. Bijvoorbeeld: een oplossing van \( x^2+1=0 \) is het complexe getal \( i \), wat een wiskundige toevoeging aan de reële getallen is die gedefinieerd is als een wortel van minus één. (Mocht je nog niet bekend zijn met complexe getallen, verwijs ik je naar deze serie, waarin ook duidelijk wordt gemaakt dat complexe getallen erg nuttig zijn in de natuurkunde.)
Alle (reële en complexe) getallen die niet algebraïsch zijn, heten de transcendente getallen. Het getal \( \pi \) is daar een voorbeeld van. Toch wist ik \( \pi \) al aan te duiden met een eindig aantal woorden, dus we dat het wél een echt getal is. Een verzameling getallen die daarom dichter bij de echte getallen komt, zijn de zogenaamde periodes. Dit zijn precies al de getallen van de vorm \( \int_{p(x)\leq a} q(x) dx \), integralen van (mogelijk hoger-dimensionale) polynomen \( p(x) \) en \( q(x) \) met rationale coëfficiënten, net als het polynoom van hiervoor. De periodes bevatten wél \( \pi \), namelijk \( \pi=\int_{x^2+y^2\leq 1} dxdy \).
Toch zijn de periodes nog niet genoeg; het wordt bijvoorbeeld vermoed dat het eulergetal géén periode is[5]. Of er een verzameling getallen is die dit getal wel bevat en zo nóg dichter bij de echte getallen komt, blijft een open vraag. Ook of de fysische getallen inderdaad de periodes bevatten is niet duidelijk; misschien is de taal van de fysische informatie namelijk wel heel anders dan onze taal. Al met al geeft het stof tot nadenken, maar voor ik daarover ga nadenken eet ik alvast de broden en de appels op, anders worden ze oud!
[1] Dit schrijft Norman Wildberger in het opiniestuk ‘real fish, real numbers, real jobs’, wat in 1999 verscheen in het tijdschrift The Mathematical Intelligencer.
[2] Een kleine subtiliteit in dit bewijs is dat we rekening moeten houden met het feit dat sommige getallen een andere decimale expansie hebben maar toch hetzelfde getal vormen, zoals we zagen met 0,9999… en 1,0000…. Daarom kunnen we voor ‘drie’ en ‘vier’ niet ‘nul’ en ‘negen’ invullen.
[3] Voor deze definitie is iets meer voorzichtigheid geboden: als we alleen met ‘gedefinieerde’ getallen willen werken, moeten we eerst netjes opschrijven wat zo’n afgeleide precies betekent.
[4] Dit heeft Eric Opdam mij verteld in persoonlijke communicatie, met de opmerking dat er veel logici zijn die hier nog veel meer over hebben nagedacht dan hijzelf. Aangaande constructies in de wiskunde zegt Opdam dat hij voor zichzelf ‘cirkels van vertrouwen’ hanteert, waarbij objecten die gedefinieerd worden aan de hand van een eindig algoritme met een in principe uitvoerbare constructie zich in de binnenste cirkel bevinden.
[5] Dit schrijven de wiskundigen Maxim Kontsevich en Don Zagier in hun artikel genaamd ‘periods’.