De padintegraal (1): het minimale-actieprincipe

Dit artikel is het eerste in een reeks over de beroemde padintegraal van de quantummechanica, waarin we hier en daar wat wiskunde niet zullen schuwen. In het tweede artikel, dat later verschijnt, zal ik nauwkeuriger de padintegraal introduceren die de quantummechanica dicteert, maar voordat we zover zijn wil ik eerst een van de meest fundamentele wetmatigheden van de klassieke mechanica bespreken: het principe van minimale actie.

Zoals Chris Ventura Meinersen al eens uitlegde in een eerder artikel, maken we in de klassieke mechanica – die de wereld op onze relatief grote schaal beschrijft – gebruik van het principe van minimale actie. In algemene zin stelt dit principe dat we voor een fysisch probleem de correcte oplossing kunnen vinden door een zogenaamde actie \( S \) te minimaliseren. In dit eerste artikel uit de reeks over de padintegraal zal ik door middel van enkele voorbeelden uitleggen hoe dit principe in de praktijk werkt.

Voor ik de actie definieer, moet ik eerst de zogenaamde Langrangiaan \(  L \) introduceren, die wordt gegeven door de kinetische energie \( T \) (ook wel bewegingsenergie genoemd) van het object dat we willen bestuderen, minus de potentiële energie \( V \):

\( L = T-V \).

De actie is nu gedefinieerd als de Langrangiaan geïntegreerd over een tijdsinterval:

\( S[x(t)] = \int_{t_1}^{t_2} L[x(t)] dt \).

Wat je met de actie \( S[x(t)] \) doet, is voor elke beweging \( x(t) \) die mogelijkerwijs plaatsvindt tussen tijdstippen \( t=t_1 \) en \(t=t_2\), een getal uitrekenen. Het principe van minimale actie vertelt ons nu dat de beweging \( x(t) \) die dit getal \( S[x(t)] \) minimaliseert – dus die het de kleinst mogelijke waarde geeft – daadwerkelijk het pad van het desbetreffende object beschrijft.

Het vinden van dit pad is een zogeheten variatieprobleem dat in essentie precies hetzelfde is als het vinden van de minima van een functie \( f(x) \). Zoals je je misschien herinnert uit de wiskundeles, moet je in dat geval eerst de afgeleide \( f’(x) \) uitrekenen en die vervolgens gelijkstellen aan nul, dat wil zeggen: de vergelijking \(f’(x)=0 \) oplossen. Ditzelfde kunnen we ook doen voor de actie \( S \). Met wat verdere wiskunde blijk dit te leiden tot de Euler-Lagrange vergelijking voor de Lagrangiaan:

\( \frac{\partial L}{\partial x}- \frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{x}} = 0 \).

In deze zogenaamde Newtoniaanse notatie laten we in veel grootheden de \( t \)-afhankelijkheid weg: zo is \( x \) de locatie, \( \dot{x} \) de snelheid en \( \ddot{x} \) de versnelling¹ van het object dat we bestuderen. De eerste term in de vergelijking hierboven is de afgeleide van de Langrangiaan \( L \) naar de positie \( x \), en de tweede term bevat een dubbele afgeleide: de Langrangiaan wordt eerst gedifferentieerd naar de snelheid \(\dot{x} \) en vervolgens nemen we de afgeleide van het resultaat naar de tijd \( t \). Hoe deze vergelijking tot stand komt is iets ingewikkelder dan bij het differentiëren van een simpele functie, en ik zal die afleiding hier dan ook niet toelichten, maar we kunnen wel kijken naar hoe natuurkundigen deze formule in de praktijk toepassen.

Neem als voorbeeld een tennisbal die zich gewichtsloos in de ruimte voortbeweegt. We kunnen in dat geval redelijkerwijs aannemen dat er bij gebrek aan zwaartekracht ook geen potentiële energie is, dus \( V = 0 \). De kinetische energie wordt gegeven door de bekende uitdrukking:

\( T =  \frac{1}{2} m \dot{x}^2\).

Oftewel: de kinetische energie – de energie die in de beweging van de bal zit – is gelijk aan een half maal de massa \( m \) van de tennisbal maal de snelheid \( \dot{x} \) van de bal in het kwadraat. Als we dan de Euler-Lagrangevergelijking construeren vinden we voor de eerste term uit die vergelijking:

\( \frac{\partial L}{\partial x} = 0 \).

De kinetische energie hangt namelijk wel af van de snelheid \( \dot{x} \) maar niet² van de positie \( x \). Nu rekenen we de tweede term in de Euler-Lagrangevergelijking uit. Allereerst vinden we uit de uitdrukking voor \( T \) dat

\( \frac{\partial L}{\partial \dot{x} } = m \dot{x} \).

Daarna moeten we differentiëren naar de tijd \( t \), wat leidt tot

\( \frac{\partial }{\partial t}\frac{\partial L}{\partial \dot{x}} = m \ddot{x}   \).

De Euler-Lagrange vergelijking vertelt ons dus dat

\( m \ddot{x} = 0 \).

De versnelling \( \ddot{x} \) moet dus nul zijn, wat betekent dat de bal met een constante snelheid in een rechte lijn door de ruimte voortbeweegt. Het feit dat iets waar geen krachten op werken op zo’n manier beweegt staat bekend als de eerste wet van Newton, maar nu hebben we die wet afgeleid met behulp van het principe van minimale actie!

Het principe van minimale actie kan nog veel meer: stel je voor dat we terug op aarde zijn – dan hebben we te maken met de potentiële energie \( V = m g \) veroorzaakt door het zwaartekrachtsveld, waarbij \( g = 9{,}81 m/s^2 \) de valversnelling is. In dat geval (reken zelf na!) geven de Euler-Lagrange vergelijkingen ons

\( m \ddot{x} = -m g \).

Die formule vertelt ons dat de versnelling \( \ddot{x} \) gelijk moet zijn aan de valversnelling³ \(  g \), wat natuurlijk precies is hoe de valversnelling is gedefinieerd. We kunnen de vergelijking ook tweemaal integreren om de precieze baan van de bal te berekenen:

\( x(t) = -\frac{1}{2} g t^2 +v_0 t +x_0\).

Dit beschrijft de bekende beweging van een bal die in de lucht wordt gegooid, met startpunt \( x_0\) en startsnelheid \( v_0 \).

Laat ik nog een derde en laatste voorbeeld met de Euler-Lagrange vergelijking oplossen: stel je voor dat de potentiaal niet lineair met \(  x \)  schaalt, zoals hierboven bij de zwaartekracht, maar kwadratisch: \( V = \frac{1}{2} k x^2 \) (waarin \( k  \)  een constante is). In dat geval (reken weer zelf na) vertellen de Euler-Lagrangevergelijkingen ons dat

\( m \ddot{x} = – k x\).

Dit is de wet van Hooke die vertelt hoe een object met een massa \( m \), bevestigd aan een mechanische veer met veerconstante \( k \), op en neer beweegt. De oplossing van deze bewegingsvergelijking kan worden uitgedrukt in termen van sinus- en cosinusfuncties die een harmonische beweging beschrijven.

Dit principe van minimale actie duikt op verschillende plaatsen op in de natuurkunde. Zoals Jeremy van der Heijden in een eerder artikel al eens uitlegde, is hetzelfde principe ook van toepassing op de breking van licht: wie een lichtstraal bestudeert die vanuit één medium (bijvoorbeeld lucht) opeens een ander medium (zoals water) binnengaat, zal zien dat de richting van de lichtstraal verandert. Een manier om deze breking van de lichtbaan te berekenen is de wet van Snellius, maar zoals Jeremy uitlegde kun je dezelfde wet ook afleiden aan de hand van Pierre de Fermats principe van minimale tijd, wat precies ons principe van minimale actie blijkt te zijn.

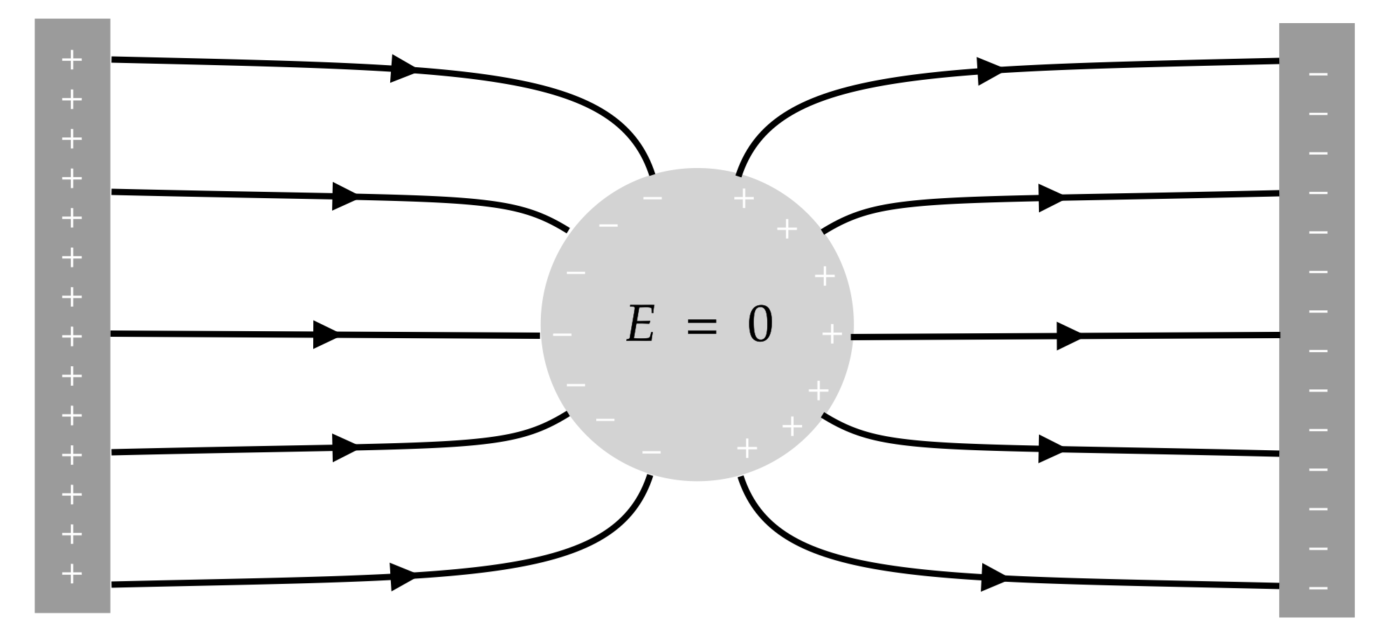
Dit soort ‘minimalisatieprincipes’, waarin een fysisch systeem een zekere grootheid probeert te minimaliseren, lijken overal in de natuurkunde op te duiken. Een ander interessant voorbeeld is dat van de elektrostatica: stel je voor dat je een grote metalen bol zou hebben en die vervolgens plaatst in een elektrisch veld, veroorzaakt door een positieve pool links en een negatieve pool rechts. De elektronen in die bol zullen dan naar links bewegen, waardoor er effectief negatieve lading zich naar links verplaatst en positieve lading naar rechts. Als gevolg daarvan wordt het elektrisch veld binnen de bol opgeheven, en is de elektrische potentiële energie effectief geminimaliseerd. Je kunt de metalen bol ook vervangen door een kooi, wat leidt tot het effect dat wij kennen als de kooi van Faraday die Damian van de Heisteeg eerder beschreef.

Weer een ander voorbeeld is de oppervlaktespanning langs de rand van waterdruppels: uit een lekkende kraan stroomt nooit een geleidelijke stroom water, maar vallen de druppels altijd één voor één. Dat komt doordat watermoleculen dipolen zijn die elkaar licht aantrekken via zogenaamde waterstofbruggen. Als gevolg is het voor een druppel energetisch aantrekkelijker om als één geheel bij elkaar te blijven, in een vorm waarin het oppervlak van de druppel zo klein mogelijk is. De waterdruppel minimaliseert dus zijn externe oppervlakte. Dit principe van minimale oppervlakken kent ook een moderne incarnatie in de studie van entropie en holografie, in termen van zogenaamde Ryu-Takayanagi oppervlakken in AdS/CFT.

Ondanks al deze mooie voorbeelden waarin de natuur de weg van de ‘minste actie’ lijkt te nemen, lijkt deze regel in de quantummechanica niet langer op lijkt te gaan, zoals de doorgewinterde QU-lezer misschien weet: volgens de quantumtheorie neemt een deeltje alle mogelijk paden van A naar B, en niet alleen het pad van de minimale actie. In een volgend artikel zullen we zien hoe het idee van ‘actie’ en een Lagrangiaan toch ook in de quantumwereld een prominente rol speelt, en leidt tot de padintegraal. We zullen zien wat de ‘statistische interpretatie’ van deze padintegraal is, en hoe de onzekerheid op de quantumschaal desondanks kan leiden tot het principe van minimale actie op menselijke schaal, waar de wetten van de klassieke mechanica gelden. Ik zou zeggen: stay tuned!

[1] Het aantal punten boven de variabele geeft het aantal tijdsafgeleiden weer. In dit voorbeeld kun je dit zien aan de eenheden van de betreffende grootheden: \( x\) wordt gemeten in meters, \( \dot{x} \) in meters per seconde en \( \ddot{x} \) in meters per seconde kwadraat.

[2] Dit kan begrijpelijkerwijs wat verwarrend zijn, aangezien je misschien denkt dat snelheid en positie niet onafhankelijk van elkaar zijn. Dat ze dat wél zijn kun je bijvoorbeeld begrijpen door te bedenken dat een object op elke mogelijke plek kan zijn, en als het op een bepaalde plek is, daar ook nog elke willekeurige snelheid kan hebben. De variabelen\( x \) en \( \dot{x} \) kunnen we hier dus zien als onafhankelijke variabelen.

[3] Merk, om het minteken te begrijpen, op dat we x naar boven – van de aarde af – hebben georiënteerd.