
Om het idee van quantumchaos uit te kunnen leggen moet ik eerst vertellen wat chaos voor klassieke systemen betekent. Met chaos bedoelen we in het dagelijks taalgebruik vaak wanorde. In de natuurkunde betekent de term ongeveer hetzelfde: we hebben het over chaos wanneer er een bepaalde wanorde in het gedrag van een systeem zit, waardoor het lastig wordt om voorspellingen te doen. Er is echter een extra voorwaarde, namelijk dat de wanorde op een precieze manier via bijvoorbeeld een vergelijking of rekenregel tot stand komt. Hoewel het systeem `onvoorspelbaar’ is, wordt het dus nog steeds vastgelegd door een onderliggende vergelijking. Zo kan een simpele recursieformule na veel herhalingen tot enorm complex gedrag leiden – gedrag dat er ogenschijnlijk chaotisch uitziet. Bekijk ook eens dit interessante artikel door Lieuwe Bakker, waarin een aantal van zulke systemen wordt doorgerekend.
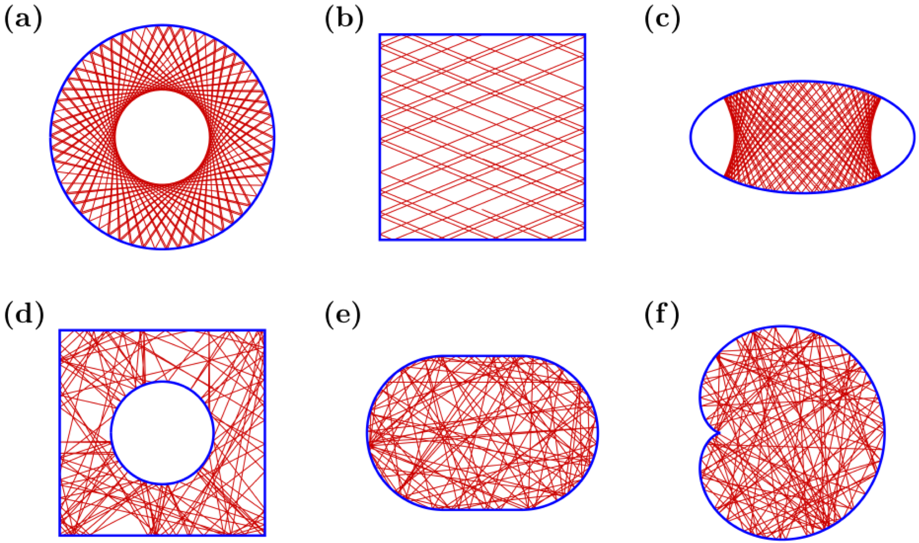
Een leuk voorbeeld van een klassiek chaotisch systeem is een biljartbal op een biljarttafel. Wie wel eens heeft gebiljart, weet dat je vaak handig gebruik kunt maken van de band die de rand van de tafel vormt. Als je weet onder welke hoek de bal de band raakt, en je geen effect gebruikt, ligt de hoek van weerkaatsing vast: in die zin is het systeem deterministisch. Toch is het niet zo makkelijk om de baan van een biljartbal te voorspellen. Voor het gemak nemen we aan dat we in een ideale situatie zitten waarin er ook geen wrijving is: de biljartbal blijft dan eeuwig doorkaatsen. Hoe ziet de typische baan van zo’n biljartbal er in dat geval uit? Dit blijkt sterk af te hangen van de vorm van de biljarttafel. In afbeelding 2 is een aantal vormen weergeven met bijhorende typische banen. Er zijn grote verschillen tussen de vormen te zien: voor sommige tafels zien de banen er redelijk geordend uit (zoals voor de ronde tafel linksboven), maar voor andere zijn ze juist heel chaotisch (zoals de tafel in de vorm van een stadion middenonder). Wat hebben de chaotische tafels met elkaar gemeen?
Het vlindereffect
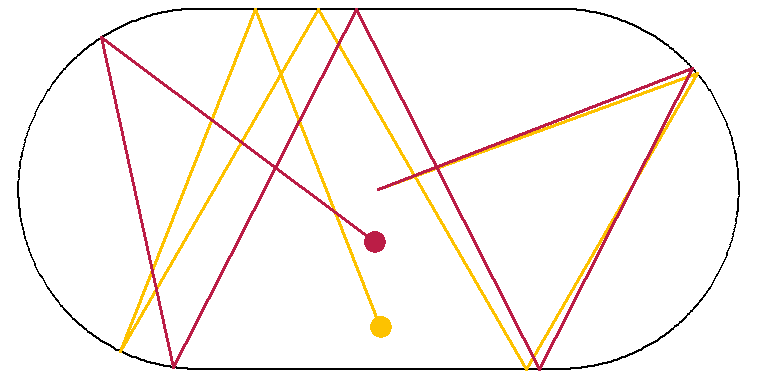
Laten we de stadionvormige biljarttafel beter bekijken. Uit dit voorbeeld halen we twee belangrijke eigenschappen van chaotische systemen. De eerste eigenschap heeft te maken met een extreme gevoeligheid van het systeem voor een verandering in de beginomstandigheden. Bijvoorbeeld: als we de richting waarin we een biljartbal wegstoten een klein beetje aanpassen, zal deze in het begin ongeveer hetzelfde pad volgen als vóór die aanpassing. Maar na verloop van tijd – meestal al na een paar weerkaatsingen – zal de baan flink gaan afwijken, en in niets meer lijken op de oorspronkelijke baan van de biljartbal. Twee banen die aanvankelijk dicht bij elkaar liggen, komen dus al snel ver uit elkaar te liggen. Dit is duidelijk te zien in afbeelding 3.
Dit verschijnsel kennen we ook uit andere systemen in de natuur. Een bekend voorbeeld is het weer. Onze weersvoorspellingen zijn gebaseerd op een ingewikkeld stelsel van gekoppelde differentiaalvergelijkingen. Gegeven de weeromstandigheden vandaag kunnen we in principe het weer van morgen uitrekenen. Dit is in de praktijk best ingewikkeld, en in de meeste gevallen zijn er geen exacte oplossingen van de onderliggende vergelijkingen bekend. We gebruiken daarom vaak een computer om de oplossing numeriek te vinden. In de jaren vijftig was het al bekend dat zulke vergelijkingen instabiel kunnen zijn: de Amerikaanse wiskundige Edward Lorenz toonde aan dat kleine foutjes in de berekening op den duur steeds groter kunnen worden.
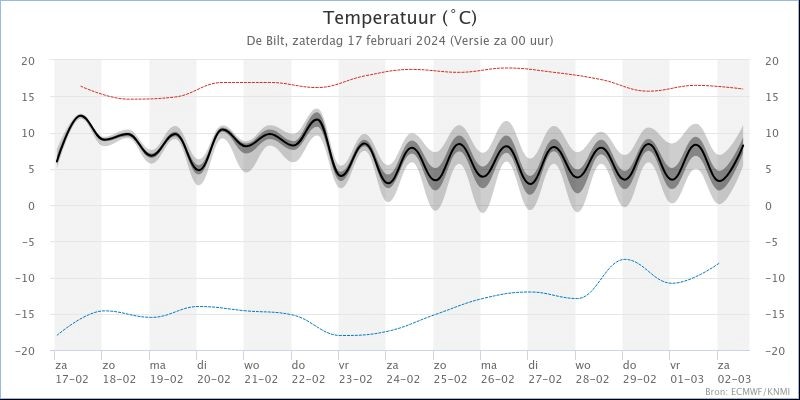
Zo kan een fout in de meting van de temperatuur vandaag – zeg van een tiende graad – in de voorspelling voor morgen tot een afwijking van bijvoorbeeld een halve graad leiden. Over een week is de fout al een paar graden, en na twee of drie weken is er geen goede voorspelling meer te doen. Dit verklaart waarom de `waaiers’ op temperatuurgrafieken – die de onzekerheid van de voorspelling aangeven – over het algemeen groter worden naarmate de datum van de voorspelling verder in de toekomst ligt – zie bijvoorbeeld afbeelding 4. Kortom: een weersvoorspelling voor morgen is een stuk betrouwbaarder dan die voor over een week. Dit effect werkt niet alleen in de tijd, maar ook met toenemende afstand. Het wordt vaak geïllustreerd met de volgende anekdote: de vleugslag van een vlinder in China kan het verschil betekenen tussen een zonnige dag in Texas of juist een orkaan. Om deze reden staat de extreme gevoeligheid voor veranderingen in begincondities ook wel bekend als het vlindereffect.
Ergodiciteit
Naast het vlindereffect is er een tweede eigenschap van chaotische systemen zoals ons biljart die te maken heeft met de baan van een individuele biljartbal. Bij sommige biljarttafels lijkt de biljartbal op den duur langs elke plek op de tafel te komen. Bij andere tafels is dit juist niet het geval en zijn er bepaalde gebieden waar de biljartbal nooit komt. Vergelijk bijvoorbeeld de ronde en de stadionvormige tafel. Het feit dat de chaotische biljartbal na verloop van tijd de gehele tafel ontdekt, staat bekend als ergodiciteit. Merk op dat dit een uitspraak is over een typische baan van een biljartbal. Zelfs op de stadionvormige tafel zijn er periodieke banen, waarbij het pad van de biljartbal zich na verloop van tijd gaat herhalen. Deze periodieke banen zijn op de chaotische tafel echter instabiel. Een periodieke baan vereist een heel specifieke beginconditie: als je deze een klein beetje verandert, leidt dit onmiddellijk tot een baan die niet periodiek is en die al snel ver van de periodieke baan afwijkt. Deze chaotische banen herhalen zich nooit, en zullen na lange tijd overal langskomen.

Ergodiciteit gaat verder dan de biljarttafel, en heeft in meer algemene systemen te maken met het concept van de faseruimte. In klassieke mechanica is de faseruimte van een systeem de ruimte van alle mogelijke begincondities. In het geval van de biljartbal wordt een punt in de faseruimte dus gegeven door twee stukjes informatie: de plek op biljarttafel en de beginsnelheid1. Aangezien iedere beginconditie leidt tot een unieke oplossing van de bewegingsvergelijking kun je de faseruimte ook beschrijven in termen van de ruimte van oplossingen van de klassieke bewegingsvergelijkingen – bijvoorbeeld met behulp van de tweede wet van Newton. De eigenschap van ergodiciteit voor een chaotisch systeem zegt nu dat een typische baan zich op den duur door de gehele faseruimte uitbreidt2, en langs ieder punt komt. Dit is een belangrijke eigenschap van klassieke chaos.
Quantumchaotisch?
Tot nu toe hebben we gekeken naar systemen die binnen het domein van de klassieke mechanica vallen: daar vormen het vlindereffect en ergodiciteit twee belangrijke pilaren voor het identificeren van chaos. Kunnen we dezelfde ideeën toepassen op een systeem dat door quantumfysica wordt beschreven? Dit blijkt knap lastig. De quantumfysica zit namelijk heel anders in elkaar dan de klassieke mechanica. Zo heeft een ‘quantumbiljartbal’ geen exacte positie of snelheid: je kunt alleen spreken over de kans om de biljartbal ergens op de tafel met een bepaalde snelheid te vinden. Het is zelfs niet mogelijk om zowel de positie als snelheid met oneindige precisie te meten. Een punt in de faseruimte heeft daarom in de quantumfysica geen betekenis; je kunt op z’n best spreken van een klein gebiedje in de faseruimte. Het blijkt dat je de faseruimte het beste kunt vervangen door de wiskundige constructie van een Hilbertruimte die golffuncties3 bevat. Wat bedoelen met het idee van ergodiciteit zodra we geen faseruimte meer hebben? Die vraag is nog niet zo eenvoudig te beantwoorden.
De quantumversie van het vlindereffect is ook niet zo makkelijk te formuleren. Dit komt door de specifieke vorm van de tijdsevolutie voor quantumsystemen: de vergelijking die vertelt hoe een golffunctie in de tijd verandert is de Schrödingervergelijking. Hoewel de Schrödingervergelijking in het algemeen erg lastig is om op te lossen, is het deel dat gaat over de daadwerkelijke tijdsafhankelijkheid relatief simpel4. Het gaat hier om een vergelijking waarin fouten over de tijd eigenlijk niet worden uitvergroot zoals het geval was bij klassieke chaos. Is er desondanks een soort quantumvlindereffect in deze situatie?
In het volgende artikel van deze reeks zal ik dieper ingaan op deze vragen, en uitleggen hoe natuurkundigen nadenken over chaos in de quantumfysica. Een belangrijke rol is weggelegd voor de Hamiltoniaan van het quantumsysteem die betrokken is bij de tijdsevolutie: deze zogeheten ‘operator’ moet op een bepaalde manier ingewikkeld genoeg zijn om tot chaotisch gedrag te leiden. Een goed begrip van quantumchaos is heel nuttig: niet alleen in de beschrijving van ingewikkelde quantumsystemen met veel deeltjes, maar ook – zoals ik in een volgend artikel zal uitleggen – om een bekend mysterie rondom zwarte gaten op te lossen.
[1] We hebben het hier over de snelheidsvector, die zowel informatie bevat over de grootte van de snelheid als de richting waarin de beweging plaatsvindt.
[2] Deze definitie hangt dus af van hoe we de faseruimte kiezen: bij het voorbeeld van de biljartbal beperken we ons tot snelheidsvectoren met vaste lengte, waarvan alleen de richting kan variëren.
[3] De golffunctie bevat informatie over de kansverdeling om de biljartbal ergens te vinden.
[4] Het tijdsafhankelijke deel van de Schrödingervergelijking is een differentiaalvergelijking met maar een enkele afgeleide naar de tijd; het plaatsafhankelijke deel heeft twee afgeleiden.