
Het eerste geval waarbij begincondities extreem belangrijk zijn wordt ook wel het ‘butterfly effect’ genoemd: een vleugelslag van een vlinder kan het hele ecosysteem van de aarde veranderen, door de begincondities op een minimale wijze aan te passen: de bijna verwaarloosbare wind die een vleugelslag met zich meebrengt. Dit fenomeen heet in wetenschappelijke termen ook wel ‘chaos’: het idee dat een systeem volledig gedetermineerd kan zijn – de vergelijkingen zijn bekend en kunnen we uitrekenen – maar toch volledig onvoorspelbaar is. In dit artikel is het mijn doel expliciet duidelijk te maken wat we precies bedoelen met “chaotische systemen”, en wat dat betekent, aan de hand van twee bekende voorbeelden: het Lorenzsysteem van vergelijkingen en de zogeheten ‘logistic map’.
Wat is chaos?
Allereerst: wanneer hebben we het over een chaotisch systeem van vergelijkingen? Technisch gezien zijn er drie aspecten waar een systeem van vergelijkingen aan moet voldoen om chaotisch te zijn. De belangrijkste eigenschap is al genoemd: het systeem moet gevoelig zijn voor initiële condities, ofwel de startwaardes. Het maakt bijvoorbeeld heel veel uit waar een object begint ten opzichte van andere objecten, en wellicht kunnen ook andere eigenschappen een enorm verschil maken, zoals de precieze temperatuur of magnetisatie. De andere twee aspecten van belang voor chaotische systemen zijn iets wiskundiger, maar zeggen zoiets als: de oplossingen van de vergelijkingen moeten in een zekere zin arbitrair dicht bij gesloten cirkelbanen (bijvoorbeeld een limietcykel!) in de “ruimte van alle toestanden” liggen, en in de loop van de tijd moeten verschillende van zulke banen met elkaar gaan ‘mixen’ (heel dicht bij elkaar komen) waardoor je de onvoorspelbaarheid krijgt. Dit zijn lastige concepten om wiskundig precies te maken; maar wellicht valt het op dat in elk geval de laatste eigenschap ook wordt geïmpliceerd door de gevoeligheid voor de begincondities. En dat klopt! In sommige gevallen is het inderdaad zo dat simpelweg de gevoeligheid voor begincondities genoeg is om te claimen dat een systeem chaotisch is. Overigens is het nog wel goed om te benadrukken dat ‘chaotisch’ niet betekent dat het systeem zich ‘willekeurig’ gedraagt. Ondanks dat het systeem zich volledig onvoorspelbaar kan gedragen, is het gedrag nog steeds volledig bepaald door een serie vergelijkingen, en dus deterministisch.
Laten we kijken naar bekend voorbeeld van een chaotisch systeem van vergelijkingen dat veel voorkomt, en expliciet duidelijk maken wat ik hierboven schreef. Het voorbeeld dat ik bedoel is het Lorenzsysteem van vergelijkingen. Voor de wiskundeliefhebbers: dat systeem van vergelijkingen ziet er als volgt uit:
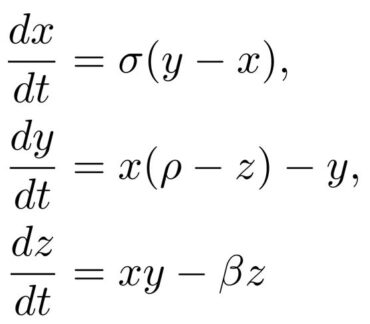
Oorspronkelijk werd dit systeem van vergelijkingen geïntroduceerd door Edward Lorenz en Ellen Fetter, als een simpel model voor atmosferische convectie. Twee zaken om te benadrukken in dit systeem zijn:
1) Het is niet lineair. Dit is te zien aan de twee niet-lineaire (kwadratische) termen in de vergelijkingen: xy en xz. Het is deze niet-lineariteit die noodzakelijk is voor een systeem om chaotisch te zijn. Een lineair systeem van vergelijkingen gedraagt zich altijd dusdanig netjes dat het nooit chaotisch gedrag kan vertonen. Aan de andere kant blijkt dat een systeem dat dergelijke niet-lineaire termen in zich heeft zeker niet perse chaotisch hoeft te zijn, en het meestal ook niet is!.
2) Een andere eigenschap die de moeite waard is om te vermelden, is dat dit systeem in drie dimensies voorkomt (met coördinaten x, y en z). Dit is belangrijke eigenschap, zo blijkt: een systeem met slechts twee dimensies kan geen chaos vertonen. Er zijn uitzonderingen mogelijk wanneer het een systeem van zogeheten discrete vergelijkingen betreft (zoals de ‘logistic map’ die we verderop in dit artikel zullen bekijken), maar in het geval van de Lorenzvergelijkingen is alles continu (met mooie doorgetrokken lijnen als je het tekent, zie de afbeelding hieronder), en heeft men dus minimaal drie dimensies nodig om chaos te krijgen.
Laten we nu dus eens kijken naar een voorbeeld mét chaos en een zonder chaos in het Lorenzsysteem. De afbeeldingen hieronder geven direct weer wat ik bedoel:
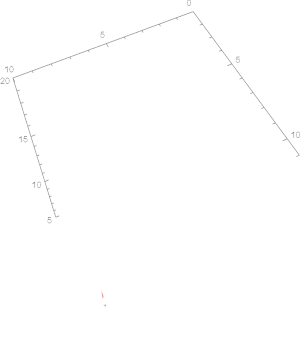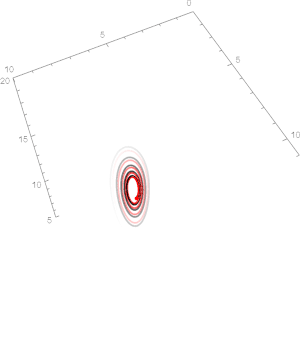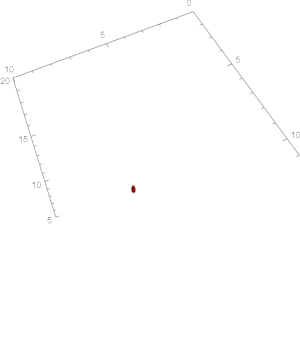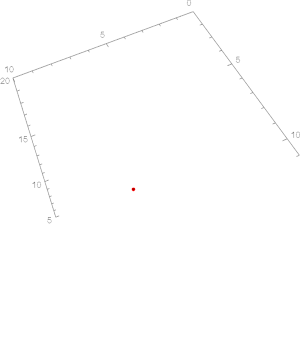

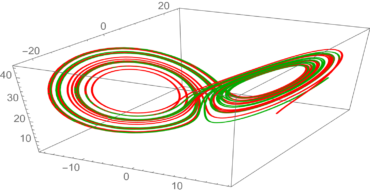
Afbeelding 3. Animatie van het Lorenzsysteem van vergelijkingen voor σ = 10 en β = 8/3. In de bovenste figuur is de waarde voor ρ gekozen als 15, en in de onderste is deze waarde 28. In de bovenste figuur is duidelijk te zien dat twee banen die allebei een groot verschil in begintoestand hebben, uiteindelijk convergeren naar hetzelfde punt. In de onderste figuur daarentegen zijn er twee verschillende banen. Beide lijnen beginnen op nagenoeg hetzelfde punt (alleen de z-coördinaat is 1/100.000 verschoven). Zoals te zien gaan in dit systeem de lijnen in de loop van de tijd zich compleet anders van elkaar gedragen: het systeem is dus gevoelig voor de begincondities, en daarmee is het een chaotisch systeem.
In de weergaven hierboven zien we een animatie van hoe het Lorenzsysteem zich gedraagt in de loop van de tijd voor verschillende keuzes van de parameters σ, ρ en β. Voor de keuze van deze parameters in de bovenste figuur gedraagt het systeem zich op een voorspelbare manier. Twee banen met verschillende begincondities convergeren in de loop van de tijd naar hetzelfde punt: niet chaotisch! De onderste figuur daarentegen gedraagt zich iets minder netjes. Twee punten die begincondities hebben die minder dan 1/100.000e van elkaar verschillen (nog kleinere verschillen kunnen ook!) zullen in de loop van de tijd compleet verschillende banen gaan inkleuren. Dit systeem gedraagt zich dus onvoorspelbaar en noemen we ‘chaotisch’.
Lyapunov-exponent
Wellicht raak je een beetje ‘geïrriteerd’ van al dit geneuzel over chaos. Het lijkt immers alsof je maar moet kijken naar een paar vergelijkingen, en dan op basis van een eigen oordeel moet vaststellen of het systeem ‘gevoelig’ is voor begincondities. Die irritatie zou niet geheel onterecht zijn, omdat het héél moeilijk blijkt om wiskundig te bewijzen dat een systeem van vergelijkingen inderdaad chaotisch is. Maar uit die formulering blijkt ook dat er technisch gezien wél een methode is om te kwantificeren of een systeem chaotisch is. Een getal waarmee je kunt aantonen of een systeem chaotisch is, is de Lyapunov-exponent. Eerst maar weer in wiskundige termen: de Lyapunov-exponent is gedefinieerd op de volgende manier:
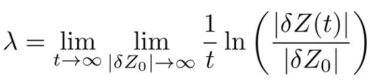
Dit is een redelijk complexe vergelijking, maar eigenlijk doet die niets anders dan wiskundig opschrijven wat het betekent als het verschil tussen 2 banen met willekeurig kleine verschillen in de begincondities, exponentieel toeneemt als je het systeem oneindig lang zou kunnen laten lopen in de tijd. Dat wil zeggen:
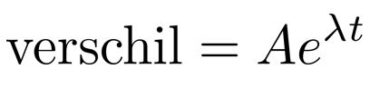
Welnu: Als de Lyapunov exponent positief is zal het verschil daadwerkelijk exponentieel toenemen in de tijd, en dus is het systeem chaotisch.
Gelukkig is het meestal mogelijk om numeriek te bepalen wat de Lyapunov-exponent van een systeem is. Om dit te doen nemen we simpelweg een systeem van vergelijkingen, lossen die stap voor stap in de tijd op, en bekijken op iedere tijdstap hoe sterk de twee systemen van elkaar verschillen en, als dat exponentieel groeit, welke λ daarbij zou horen. Hieronder zie je een voorbeeld van de Lyapunov-exponent van een Lorenzsysteem. Als we het systeem oneindig lang zouden kunnen laten lopen, zouden we uiteindelijk de ‘echte’ waarde van de Lyapunov-exponent vinden, maar in de praktijk moeten we het doen met een benadering:
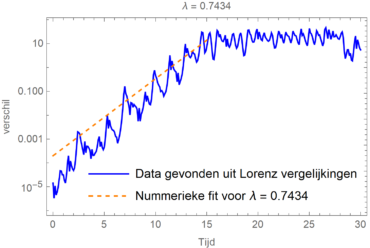
Er zijn nog vele andere voorbeelden van chaotische systemen. Een ander bekend voorbeeld is de logistic map:
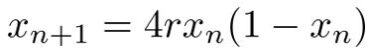
De logistic map is een iets ander voorbeeld van chaos, aangezien dit om een discrete vergelijking gaat: de oplossing is geen continue functie, maar een discrete reeks van getallen xn. De vergelijking heeft echter dezelfde eigenschap: dat voor een bepaalde keuze van r, het systeem zich compleet anders kan gaan gedragen voor verschillende begincondities zoals te zien in de animatie hieronder. De punten geven aan waar een bepaalde waarde van x0 terecht gekomen is voor verschillende waardes van r. Zoals te zien gedraagt het systeem zich tamelijk chaotisch als r (grofweg) groter is dan 0,9.
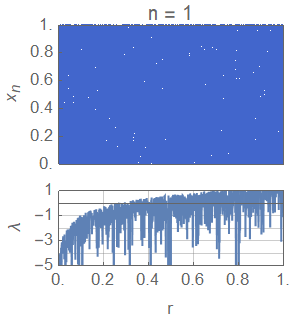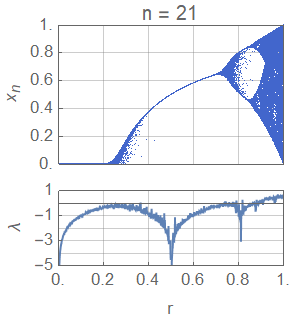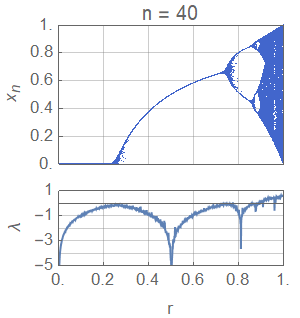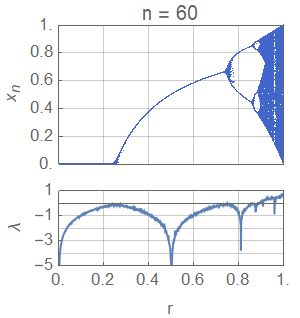
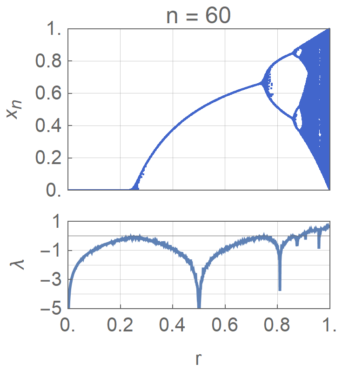
Hieronder zie je een plaatje van de bijbehorende Lyapunov-exponenten. Zoals te zien is, is de Lyapunov-exponent positief in de regionen waar er veel chaos te zien is, precies zoals we verwachten. In de afbeelding komt de rode lijn uit het onderste diagram boven 0 uit in de gebieden waar de bovenste afbeelding een wirwar van punten is.
Als laatste zou ik de lezer willen wijzen op het volgende youtube filmpje van numberphile (één van mijn favoriete kanalen op Youtube). Hierin laat een wiskundige een hele reeks voorbeelden zien van simulaties van systemen die chaotisch zijn – op een veel mooiere manier dan ik zou kunnen! Een intrigerend schouwpel. Dus mocht je chaotische systemen als theoretische modellen niet zo interessant vinden, dan zijn de plaatjes alsnog wel de moeite waard!