
Here, we will make a completely different point, namely that the gravitational force, as Einstein taught us, emerges from the geometry of space and time itself. In the next and final part we will then combine both ideas and see how string theory leads to a natural description of quantum gravity.
The Mystery of Gravity
In 1687, Isaac Newton, in his Philosophiæ Naturalis Principia Mathematica, wrote down the first formula that described the universal force of gravity. It takes the form
\( F= \frac{GmM}{r^2} \).
This little formula describes the gravitational force between two massive objects of masses \( m, M \), which sit at a distance \( r \) from another. The law is universal because the strength of the gravitational force is the same for all objects, which is encoded in the fact that Newton’s constant \( G \) is always the same. This equation was a revolutionary step towards the understanding that nature has some underlying structure, a set of fundamental laws that could explain it. Newton’s law of universal gravitation explained not only why apples fall from trees, but also why celestial objects like the planets stay in orbit.
The remaining question, however, is not what the force of gravity is, but how gravity can exert that force! How is it possible that the moon is kept in orbit by its attraction to earth’s gravitation if it is 384,000 km away? The answer to this question is curvature.
Paths in Spacetime
The question of how gravity exerts its force is explained by the geometry, meaning curvature, of spacetime. This affects how things move in spacetime. Let’s look at how we can probe the curvature of a simple space, like a sphere (think of the Earth’s surface), by following two different paths on it.
The basic idea is that we start out at some location on the sphere, we take the equator in the figure, and follow two different paths to the north pole. At the same time we draw arrows that always point towards the north pole.
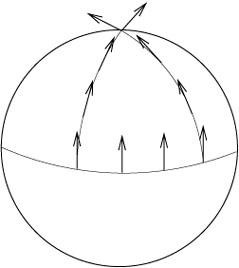
If we trace out both paths we see that, as they come closer to the north pole, the arrows begin to point in totally different directions. This is due to the fact that the sphere is not a flat surface, but it has some curvature.
We see that the curvature of the sphere made the paths change their trajectory: they started as parallel lines and then ended meeting at the north pole with a nonzero angle to one another. This is reminiscent of what gravity does: it curves the paths of objects. Do not let this example of the sphere confuse you and make you believe that due to gravity we will all move towards the north pole. The only point here is that curved spaces behave like spacetime does because of gravity. The relevant question therefore is which curved space(-time) describes our world?
To answer that question it might be helpful to look at planetary orbits. For example, the moon’s orbit around Earth is described by the curved space generated by Earth’s presence, as illustrated in the following figure1.
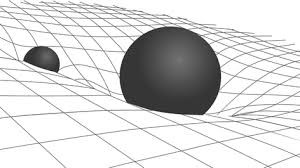
By this bend in the spacetime fabric, we see that one can describe the moon’s orbit as a result of the ’valley’ that Earth creates. The moon just travels along the slope. Additionally we see that the moon also creates a bend, although a smaller one. Nevertheless both objects bend spacetime. This means that something that the two have in common must be responsible for creating the curvature. That thing is mass! And the amount of mass determines the amount of curvature. We also know, by Newton’s universal law of gravitation, that as an object becomes more massive, its gravitational field becomes stronger. By combining these ideas we hence find ourselves with a fundamental idea of Einstein’s theory of general relativity: Gravity comes from the curvature of spacetime.
Dynamic Geometry and Quantum Gravity
The last ingredient in this story is that things change and interact, even spacetime. As everything in our universe is in motion, we find that gravity and hence the geometry of our universe changes constantly. This is stated nicely in a quote from the physicist John Wheeler:
Spacetime tells matter how to move;
matter tells spacetime how to curve.
Gravity is a constant back and forth between these two quantities.
Now that we know that geometry and gravity are, at least on a large scale like that of planets and apples, the same. But we might wonder what gravity looks like on the quantum scale, i.e. what quantum gravity really is. Although we do not know for certain, we know it must have similar ingredients as the theory of general relativity. The concept of geometry playing the role of the cause of gravitational interactions should therefore be included. Also the notions of Feynman diagrams and how they explain interactions should be important in our description. These two ideas guide us to the following recipe:
- We need to have some particle that carries the gravitational interaction,
- These interactions should somehow be related to the geometry of spacetime,
- We need to compute an infinite number of Feynman diagrams, which should then represent all types of spacetime geometries.
Given this partial recipe, we now need to find a theory which contains these ingredients and also ultimately describes our world. One candidate for such a theory is string theory.
Résumé et partie finale
What have we learned so far, before heading to our last destination, namely part 3 of this mini-series?
- Einstein taught us that gravity is a result of the curvature of spacetime. We saw this in the example of the moon’s orbit and how earth’s gravitational field affects the geometry of the spacetime fabric.
- Feynman diagrams hint at the fact that the gravitational interaction might be carried by a particle. That particle would somehow be connected to the geometry and hence the curvature of spacetime.
Let’s find out next time how, in the light of these ideas, string theory may become the successful theory to describe quantum gravity!
[1] This is of course only an illustration. In reality the 4-dimensional space-time is curved and not only some 2d sheet underneath the planets.