
Now we want to combine both ideas and see how the interactions of strings lead to a quantum theory of gravity.
Strings vs particles
So far we have encountered the interaction of two electrons, which repel each other by exchanging a photon, which by itself could do all sorts of things. To express the full scattering process one needs to take into account all possible things that can happen. In order to describe these interactions we made use of Feynman diagrams.
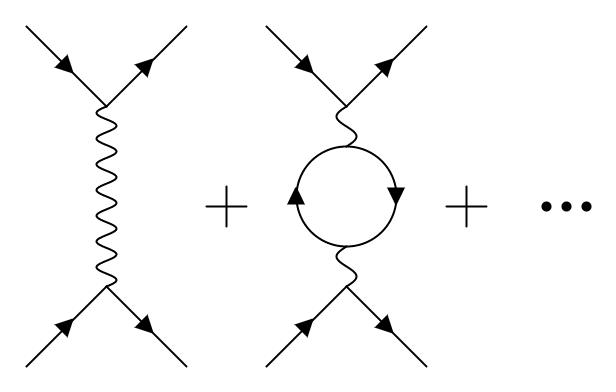
Regarding the problem of quantum gravity, however, pointlike particles, like electrons and photons, do not have the properties that physicists believe the quanta of gravity, namely the force-carrying gravitons, should have.
This brings us to string theory, where, instead of pointlike particles, we consider all fundamental particles to be extended objects, namely the infamous strings. Like a guitar string, these strings can also be plucked leading to different vibrations. Amazingly, if the string forms a closed loop one finds that the way the string vibrates can reproduce the properties of the elusive graviton!

Additionally, we can study the quantum collisions of these strings, as we did for the electrons, and find their ‘stringy’ Feynman diagrams:

But how is this related to a theory for quantum gravity?
Quantum Gravity
The exceptional fact is that these diagrams illustrate the quantum interactions of strings, which can be linked to the curvature of spacetime and hence gravity.
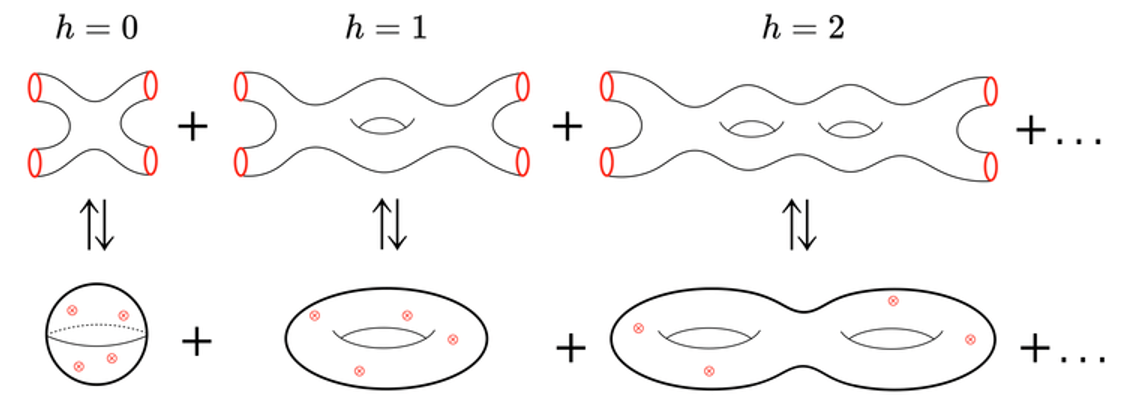
In the ordinary, non-stringy case we saw that the additional diagrams described the fluctuations of the electromagnetic field (the photon field). Here we see that the interaction of strings leads to additional stringy diagrams, which are labelled by the number of holes analogously to the way the power of the electric charge appeared in the ordinary Feynman diagrams.
When looking at the first diagram (labelled by \(h = 0\)) we see that, as the two strings interact, they merge and excite a graviton, which then decays into two strings again. Importantly, as strings are thought to be the fundamental constituents of all particles, we see that all particles interact through a universal force: the known gravitational force. From our understanding of ordinary Feynman diagrams we can then observe that the additional stringy Feynman diagrams describe the fluctuations of the gravitational field (the graviton) and therefore describe the quantum-mechanical behaviour of gravity.
Et voilà, by looking at the stringy Feynman diagrams of interacting closed strings, we arrived at a quantum theory for gravity! String theory allows us to describe the quantum-mechanical behaviour of what Einstein taught us more than a century ago. But there are still some mysteries regarding strings and gravity. For those who are intrigued about how this story continues I refer you to Marcel Vonk’s Strings and Holography series.