
Als je te lang op een matras ligt, kunnen er op bepaalde plekken kuilen ontstaan. Een oplossing is om het matras eens in de zoveel tijd in een andere positie te leggen, zodat je niet steeds op dezelfde plek ligt. In het ideale geval zou je een handeling bedenken die je keer op keer kunt herhalen, zodat je niet hoeft te onthouden wat je de vorige keer precies hebt gedaan. Maar wat is de beste manier om dit te doen? Draai je het matras zodat het voeteind en hoofdeind worden verwisseld, of keer je het helemaal om? Of doe je een gecombineerde versie, waarbij je zowel het matras keert als ronddraait? En doe je zo eigenlijk iets wat je niet in een enkele handeling had kunnen doen?
Matraswiskunde
Een matras heeft twee kanten waarop je kan slapen, en een bepaalde oriëntatie – afhankelijk van welke kant van het matras naar het voeteind is gericht: een totaal van twee maal twee is vier verschillende `matrastoestanden’ dus. We zijn op zoek naar een handeling die bij herhaling alle mogelijke toestanden van het matras langsgaat, en pas dan weer terugkomt bij de oorspronkelijke situatie. Op deze manier wordt het matras zo gelijkmatig mogelijk beslapen. We noemen zo’n handeling cyclisch, omdat deze bij herhaling de gehele cyclus van alle mogelijke matrastoestanden doorloopt. Kunnen we voor het keren van een matras zo’n cyclische handeling bedenken?
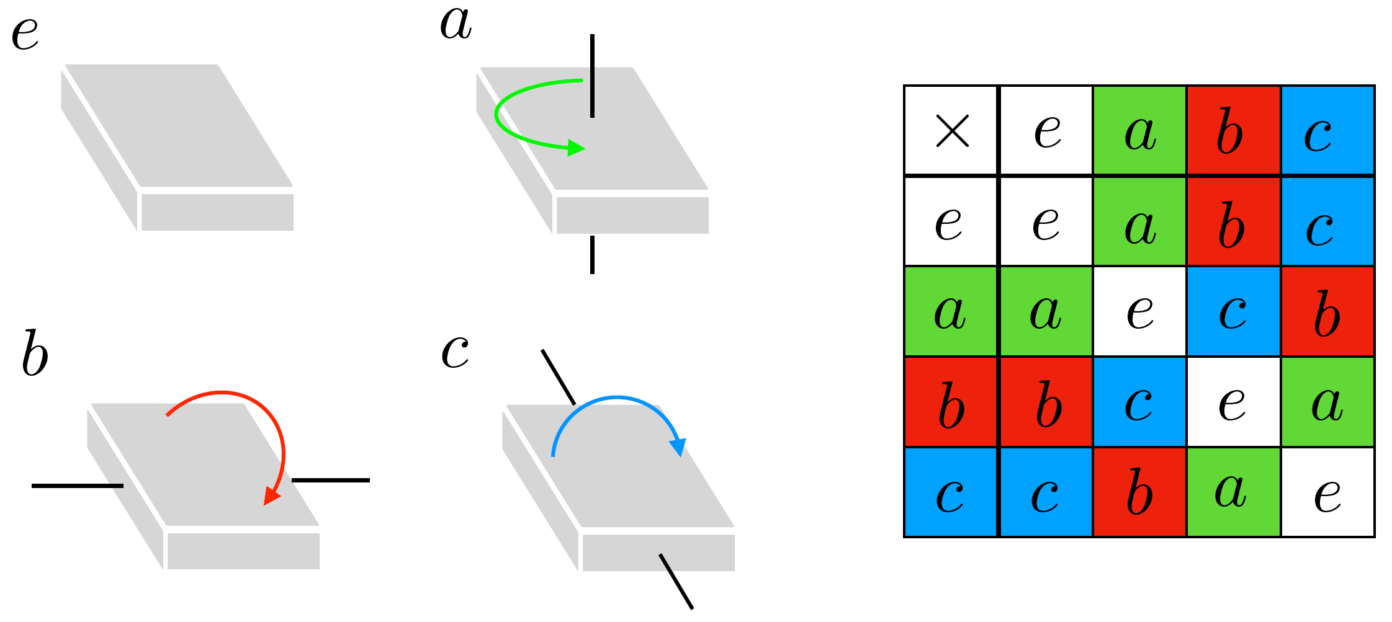
Eerst moeten we weten wat we überhaupt met het matras mogen doen. Een voorwaarde is dat het matras na de handeling nog steeds op het bed past. We bekijken een drietal `basishandelingen’ – ook wel generatoren genoemd – die we definiëren aan de hand van de drie symmetrieassen van het matras. Als we het matras 180 graden draaien langs een van de drie assen, vinden we een symmetrie. De beginsituatie ziet er namelijk precies zo uit als de eindsituatie. De verschillende basishandelingen zijn in afbeelding 2 (links) weergeven: een draai van 180 graden zonder te keren (a), omkeren over de lange kant (b) en omkeren over de korte kant (c). Ook `niets doen met het matras’ (e) zien we als aparte basishandeling.
Het is niet zo moeilijk om in te zien dat geen van de basishandelingen cyclisch is. Als je het matras namelijk twee keer over dezelfde as draait, kom je weer terug in de oorspronkelijke situatie. Daarmee alterneer je tussen twee toestanden, en niet vier. Maar wellicht is het wel mogelijk om een cyclische handeling te bedenken door verschillende basishandelingen te combineren – door bijvoorbeeld een draai gevolgd door een keer uit te voeren.
Groepentheorie
De bovenstaande vraag kunnen we beantwoorden zonder dat we daadwerkelijk iets met een matras hoeven te doen. We hebben alleen een beetje wiskunde nodig: in dit geval het vakgebied dat over wiskundige symmetrieën gaat, groepentheorie. Abstract gezien is een groep een verzameling van objecten, die we elementen noemen, en een manier om ze te combineren, een zogenaamde vermenigvuldiging. De elementen van de `matrasgroep’ zijn de handelingen die je met het matras kunt uitvoeren. De regel om twee handelingen met elkaar te vermenigvuldigen is simpelweg dat je ze na elkaar uitvoert.
Niet iedere verzameling van operaties vormt overigens een groep. Er moet aan een aantal regels worden voldaan. Zo moet de verzameling een element bevatten dat niets doet: een operatie die de toestand van het systeem hetzelfde laat. Voor het keren van matrassen geven we deze handeling aan met de letter ‘e’. (Voor andere groepen overigens ook – vandaar de bijzondere label-keuze e-a-b-c in afbeelding 2.) Daarnaast moet ieder object in de groep een inverse hebben: een handeling die de oorspronkelijke handeling tenietdoet. Dit geldt ook voor matrassen. Iedere draai of keer is namelijk zijn eigen inverse: als je het matras keert, en dan precies hetzelfde nog een keer doet, kom je weer terug in de oorspronkelijke situatie. In formulevorm wordt dit uitgedrukt als:
\( a \cdot a = e, \qquad b \cdot b =e, \qquad c \cdot c = e \).
Nog een belangrijke regel is dat voor twee handelingen in de groep de vermenigvuldiging van beide handelingen ook in de groep zit. In wiskundige termen zeggen we dat de groep gesloten is. Een voorbeeld: een draai ‘a’ gevolgd door een keer over de lange kant, ‘b’, geeft hetzelfde als een keer over de korte kant ‘c’. In de groep geldt dus de volgende regel:
\( b \cdot a = c \).
Het is in de wiskundenotatie gebruikelijk om bij het samenstellen van operaties de eerste operatie – in dit geval ‘a’ – rechts te schrijven, en de operatie die je daarna uitvoert – ‘b’ – links: tegen de leesrichting in dus.
De verschillende manieren om de elementen van een groep met elkaar te vermenigvuldigen worden vaak in een vermenigvuldigingstabel weergeven. De vermenigvuldigingstabel van de matrasgroep is in afbeelding 2 (rechts) te zien. Je leest zo’n tabel als volgt af: het resultaat van een vermenigvuldiging tussen twee elementen vind je door in het vak behorende bij de rij en de kolom van beide elementen te kijken. Bijvoorbeeld: in de doorsnede van de rij ‘a’ en de kolom ‘b’ vinden we inderdaad de handeling ‘c’. We kunnen nu eindelijk een antwoord geven op de oorspronkelijke vraag. Omdat we al weten dat geen van de generatoren cyclisch is, weten we dit nu ook voor elke combinatie van generatoren: hoe lang of ingewikkeld je zo’n handeling ook maakt, je kunt deze – door stap voor stap gebruik te maken van de vermenigvuldigingstabel – reduceren tot een van de basisoperaties. Als oefening kun je bijvoorbeeld zelf nagaan dat:
\( a \cdot b \cdot b \cdot b \cdot c \cdot a \cdot c = b \).
Met de bovenstaande observatie – dat iedere combinatie van basishandelingen weer een basishandeling is – hebben we wiskundig bewezen dat er voor de matrasgroep geen cyclische handeling bestaat! Helaas is er dus geen draai of keer te vinden die je eens in de zo veel tijd kunt herhalen, zodanig dat je cyclisch langs alle toestanden van het matras gaat.
Het wisselen van autobanden
Niet alle klusjes in het huis zijn even ingewikkeld: voor het doorwisselen van je autobanden bestaat bijvoorbeeld wél een simpel cyclisch trucje. Verplaats alle banden bijvoorbeeld een plek tegen de klok in: de band rechtsvoor naar rechtsachter, rechtsachter naar linksachter, enzovoort. Als je dit proces vier keer herhaalt, ben je weer terug in de oorspronkelijke situatie, en is elke autoband langs iedere hoek van de auto geweest. Daarmee is er voor het doorwisselen van je autobanden wel een cyclische handeling te vinden. (Terzijde: je hebt dan niet elke mogelijke configuratie van de banden gehad – bijvoorbeeld niet die waarbij je twee banden met elkaar verwisselt en de andere twee op hun plek laat – maar elke band is wel op elke plek geweest.) In afbeelding 3 zijn de verschillende operaties uit deze `autobandgroep’ weergeven. Eenmaal doordraaien wordt aangegeven met een \( r \), tweemaal met \( r^2 \) en driemaal met \( r^3 \). Bij vier keer doordraaien zijn we weer terug in de originele situatie.
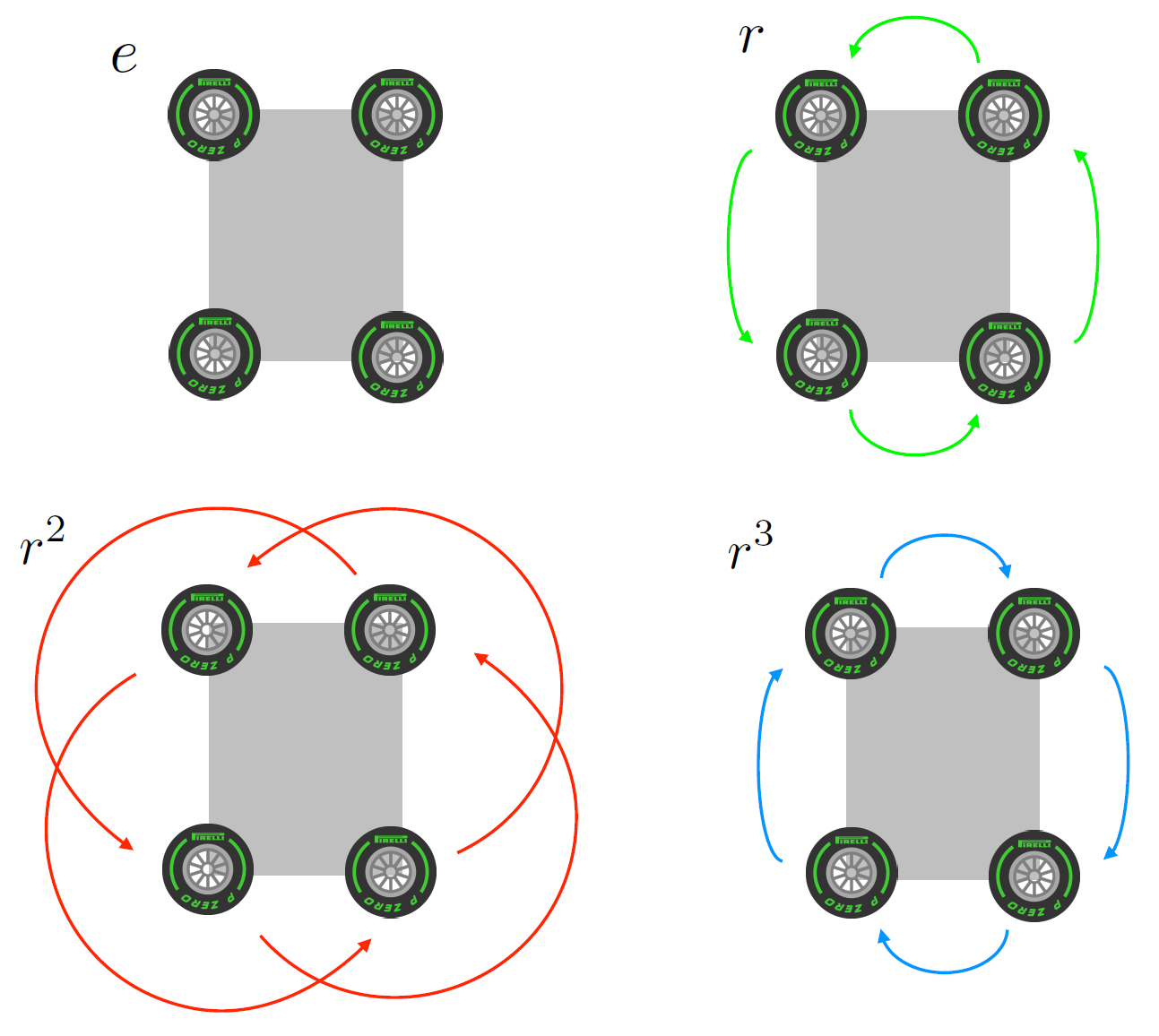
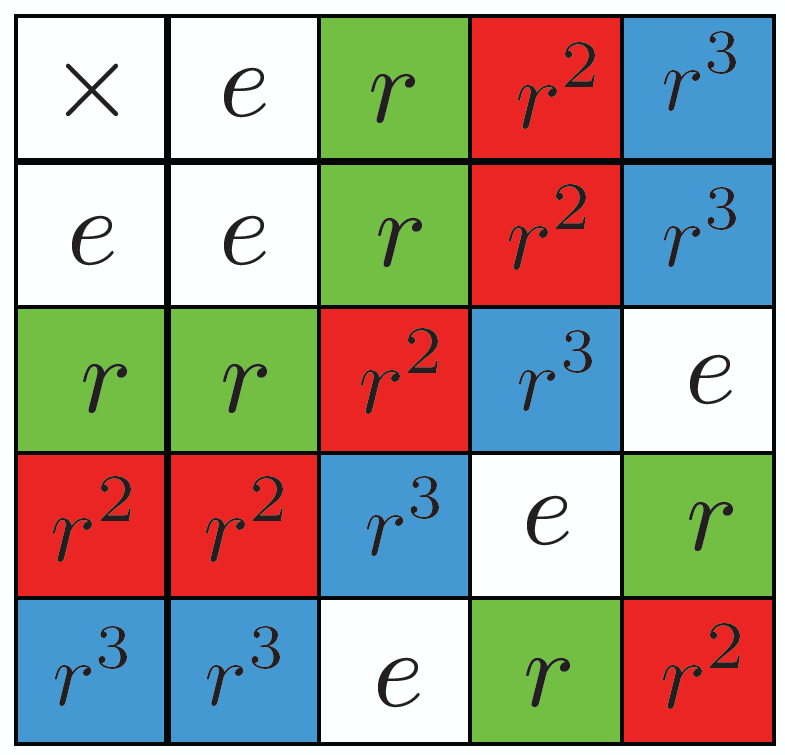
De autobandgroep bestaat net als de matrasgroep uit vier elementen. Waarom zijn het doorwisselen van een autoband en het keren van een matras dan toch verschillend? Het antwoord blijkt opnieuw in groepentheorie te liggen. De matrasgroep staat bij wiskundigen ook wel bekend als de viergroep van Klein, naar de Duitse wiskundige Felix Klein. De autobandgroep heet de cyclische groep bestaande uit vier elementen. Het blijkt dat beide groepen wiskundig verschillend zijn1. Dit kun je bijvoorbeeld zien door de kleurstelling van beide vermenigvuldigingstabellen (in afbeelding 2 en 4) te vergelijken: voor de matrasgroep geldt bijvoorbeeld groen x groen = wit, maar voor de autobandgroep geldt daarentegen dat groen x groen = rood.
De groepen hebben wel gemeenschappelijk dat hun vermenigvuldigingstabel symmetrisch is ten opzichte van de diagonaal. Dit betekent dat de volgorde waarin je de handelingen uitvoert niet uitmaakt voor het eindresultaat. Een groep waarbij dit het geval is noemen we abels, naar de Noorse wiskundige Niels Henrik Abel. Er blijken dus twee verschillende abelse groepen met vier elementen te bestaan – en daarom is banden verwisselen niet hetzelfde als je matras draaien. De cyclische groep en de viergroep van Klein zijn overigens wel de enige groepen met vier elementen: je kunt wiskundige bewijzen dat er geen enkele andere manier is om vier operaties te combineren en ook aan alle groepsregels2 te voldoen.
Samenvattend: we hebben gezien hoe een simpele vraag over matrassen kan leiden tot heel interessante wiskunde. In de zoektocht naar een ideale matraskeer hebben we niet per se gevonden wat we wilden, maar we hebben wel een aantal belangrijke dingen over groepen geleerd: in het bijzonder over de viergroep van Klein en de cyclische groep. Mocht je enthousiast zijn geworden over dit onderwerp, dan kun je ook eens kijken naar dit eerdere artikel over een nog veel complexere groep: de zogenaamde monstergroep. Al is die groep – om duidelijke reden – minder geschikt voor het slapengaan.
[1] We zeggen dat beide groepen niet isomorf zijn.
[2] Een laatste groepsregel – die we nog niet hebben genoemd – is associativiteit van de vermenigvuldiging. Deze regel is iets lastiger uit te leggen in woorden, omdat hij voor het ‘na elkaar doen’ van handelingen automatisch waar is, maar zegt in formulevorm zoiets als:
\( a \cdot (b \cdot c) = (a \cdot b) \cdot c \).