
De Einsteinvergelijkingen vertellen welke vormen de ruimtetijd allemaal aan kan nemen. In Minkowski-ruimte, platte ruimte zonder kosmologische constante, zijn die Einsteinvergelijkingen heel kort op te schrijven:
\( R_{\mu \nu} = 0 \).
Deze formule zegt dat alle componenten van de zogeheten Riccitensor gelijk moeten zijn aan nul. In \(d\) dimensies zijn dit \(d(d+1)/2-1\) onafhankelijke vergelijkingen. In vier dimensies (drie ruimtedimensies en één tijddimensie) zijn er dus 9 onafhankelijke vergelijkingen. Daar weten we bovendien dat de enige statische oplossing met een “zwart object” erin die van het bolvormige zwarte gat is. Maar hoe zit dit in andere aantallen dimensies?
Volgens de snaartheorie bestaat ons universum niet uit slechts vier, maar wel 10 dimensies, en volgens M-theorie zelfs uit 11! Hoe valt dit te rijmen met de wereld die we om ons heen zien, met slechts drie ruimtedimensies: lengte, breedte en hoogte, en één tijddimensie? Zoals al eerder uitgelegd in dit artikel van Damian van de Heisteeg, kunnen we de extra dimensies begrijpen als opgerolde dimensies. Voor een koorddanser lijkt het koord waar hij of zij overheen loopt ééndimensionaal: de koorddanser kan alleen naar voor of naar achter bewegen. Maar voor bijvoorbeeld een mier op het koord is het tweedimensionaal: zo’n mier kan ook om het koord heen, langs de onderkant. Dit is ook hoe vanuit de snaartheorie wordt gedacht over de missende dimensies: als ze heel klein en opgerold zijn, is er in het dagelijks leven weinig van te merken. Deze opgerolde extra dimensies zijn alleen relevant als we inzoomen tot de schaal van de opgerolde dimensie.
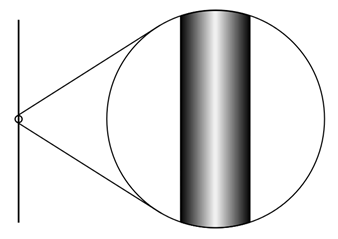
Afbeelding 2. Compactificatie. Het tweedimensionale oppervlak van het koord ziet er van veraf uit als een ééndimensionale lijn. Afbeelding: Alex Dunkel.
Stel nu dat we zwarte objecten bestuderen in niet vier maar in vijf dimensies. De Einsteinvergelijking heeft dan niet 9 maar 14 onafhankelijke componenten. Als we ervan uitgaan dat niets verandert als je je verplaatst in die extra dimensie, dan zijn we weer terug bij de 9 oorspronkelijke vierdimensionale Einsteinvergelijkingen, waarvan het zwarte gat de enige oplossing was.
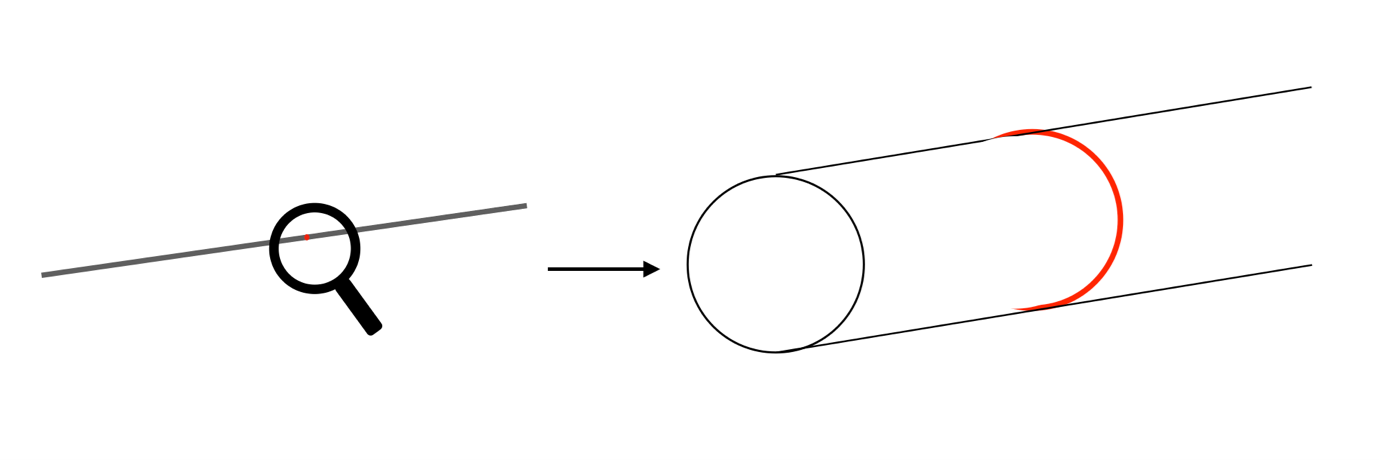
Maar de vijfdimensionale ruimtetijd ziet er nu anders uit dan gewoon een zwart gat in vijf dimensies. Terug naar het voorbeeld van twee dimensies: stel je voor dat ergens op het koord een rode stip zit. Niets hangt af van de opgerolde dimensie, dus ingezoomd zal deze stip langs de extra dimensie een cirkel zijn geworden – zie afbeelding 3. Hetzelfde principe gaat op met ons vierdimensionale zwarte gat dat niet afhangt van de vijfde dimensie: in plaats van een zwart gat is het nu een zwarte ring geworden!
Het antwoord op de vraag of bepaalde objecten echt kunnen bestaan, hangt niet alleen af van of ze een oplossing zijn van de Einsteinvergelijkingen. Zodra zich in de ruimtetijd andere, bewegende objecten bevinden, zullen deze zorgen voor (vaak minuscule) zwaartekrachtsgolven. Als een zwaartekrachtsgolf op een zwart gat botst, zal het zwarte gat een tijdje trillen. Deze trillingen doven langzaam uit en erna zal het zwarte gat nog steeds een zwart gat zijn: het is stabiel onder kleine verstoringen.
Voor een zwarte ring ligt de situatie iets anders. De wetenschappers Ruth Gregory en Raymond Laflamme hebben in dit artikel uitgerekend wat er gebeurt als er kleine trillingen op zo’n zwarte ring botsen. In tegenstelling tot wat er bij een zwart gat gebeurt, waar de trillingen langzaam uitdoven, ontdekten zij dat bij een zwarte ring de verstoring juist groter wordt naarmate tijd vordert! Dit betekent dat zo’n zwarte ring instabiel is. In onderstaand filmpje van GRChombo wordt gesimuleerd wat er gebeurt met zo’n zwarte ring als die wordt verstoord:
Je ziet dat de zwarte ring na verloop van tijd splitst in meerdere zwarte gaten. Een andere mogelijke eindconfiguratie van de zwarte ring is dat het een enkel vijfdimensionaal zwart gat wordt. Dit fenomeen, dat zwarte ringen in opgerolde dimensies uiteindelijk bolvormige zwarte gaten vormen, wordt de Gregory-Laflamme-instabiliteit genoemd.
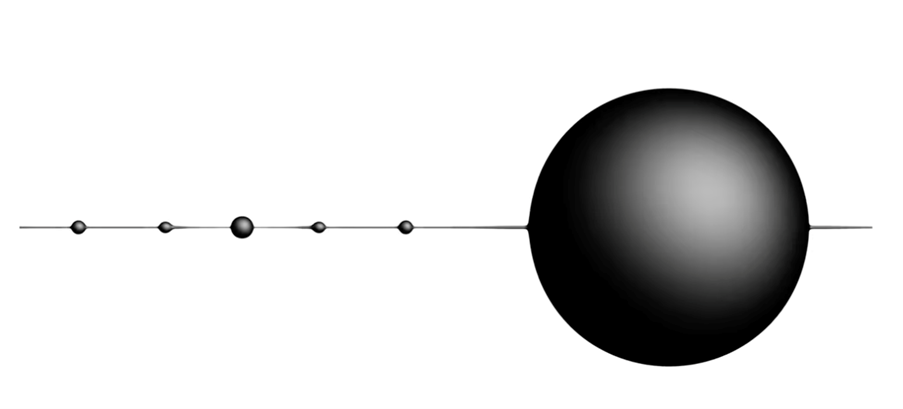
In de simulatie blijven de verschillende zwarte gaten nog wel door een heel dunne “zwarte snaar” verbonden. Dit komt doordat de berekeningen waarop de video is gebaseerd alleen klassieke aspecten van zwaartekracht meenemen. Als de zwarte gaten echt zouden afsplitsen, zou iets ontstaan wat we een “naakte singulariteit” noemen. Natuurkundigen geloven dat dit in de natuur nooit echt zal gebeuren; dit wordt het principe van ‘kosmische censuur’ genoemd, en is eerder besproken in bijvoorbeeld dit artikel van Evita Verheijden. Aangezien dit probleem zich voordoet als de straal van de zwarte snaar heel klein is, is de verwachting is dat een beter begrip van de quantumzwaartekracht deze problemen zal oplossen en dat er geen naakte singulariteiten ontstaan, in overeenstemming met de kosmische censuur.
Vanuit de tiendimensionale snaartheorie verwachten we niet één, maar meerdere opgerolde kleine dimensies – zes, om precies te zijn. Hierboven hebben we al gezien dat een enkele extra dimensies zorgt voor onverwachte dynamische effecten, en dit blijft het geval als we meerdere dimensies toevoegen. Hoe die extra dimensies precies zijn opgerold maakt daarbij nogal wat uit. Er zijn heel veel manieren waarop je zes dimensies kan oprollen, en dit is een van de aspecten die het zo moeilijk maakt om voorspellingen te doen vanuit snaartheorie: een andere manier van oprollen zorgt voor heel andere eigenschappen van de effectieve theorie in vier dimensies.
Of ons universum daadwerkelijk zes van die opgerolde dimensies bevat is nog niet duidelijk: misschien dat deeltjesversnellers hier ooit een antwoord op kunnen geven. Vanuit de snaartheorie wordt het in ieder geval wel verwacht, en als de opgerolde dimensies heel klein zijn, is het niet gek dat we ze nog niet gezien hebben. Pas bij heel hoogenergetische botsingen zullen de effecten van deze mogelijke extra dimensies gemeten kunnen worden. Het feit dat snaartheorie tien dimensies nodig heeft is voor theoretisch natuurkundigen dus niet zo’n probleem; het zou een groter probleem zijn als de theorie alleen in drie dimensies (waaronder de tijd) of minder zou werken. Want waar het aantal effectieve dimensies wel láger kan worden door oprollen, kan er niet zomaar een dimensie bijkomen!
Of we zulke extra dimensies dus ooit zullen waarnemen is voorlopig nog een open vraag. Het is in ieder geval interessant om te zien wat de effecten van zulke extra dimensies kunnen zijn in ‘onze eigen’ vier dimensies – en voor de “zwarte objecten” die we daarin tegen kunnen komen.