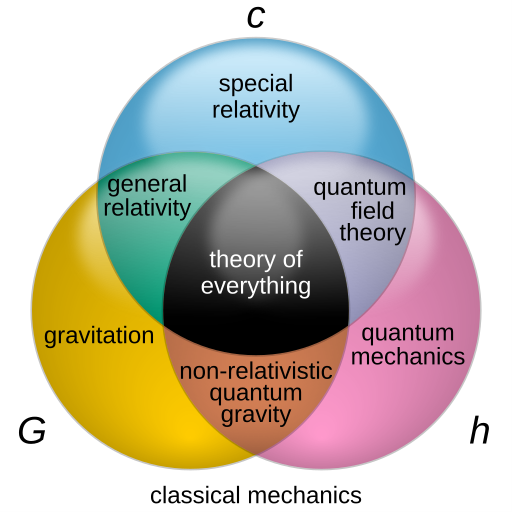
Om de verschillende aanpakken voor quantumzwaartekracht goed uit te kunnen leggen, zal ik eerst verder inzoomen op het probleem zelf. Theoretisch natuurkundigen beschikken over twee zeer succesvolle theorieën over de fundamenten van het heelal: algemene relativiteitstheorie en quantummechanica. Algemene relativiteit beschrijft hoe de ruimtetijd en massa elkaar beïnvloeden. In het bijzonder stelt de theorie dat de ruimtetijd dynamisch is: ruimtetijd verandert, en die verandering wordt beschreven door een aantal deterministische wetten. Dat wil zeggen dat als je op een bepaald moment de precieze toestand van de ruimtetijd kent, je in principe ook de precieze toestand kan uitrekenen op een later moment. Daarentegen is quantummechanica inherent probabilistisch: zelfs als je de toestand op een gegeven moment exact kent, kun je op zijn best de kansen op bepaalde meetresultaten op een later moment uitrekenen. Ook is de quantummechanica gedefinieerd op een vaste achtergrond: in de theorie wordt aangenomen dat de ruimtetijd niet verandert.
Tot op zekere hoogte werken beide theorieën extreem goed – bijvoorbeeld in situaties waar één van de twee een verwaarloosbaar kleine rol speelt. Dit is bijvoorbeeld het geval als je wil uitrekenen wat er gebeurt als twee atomen op elkaar botsen. De massa van de atomen is zo klein dat de verandering van de ruimtetijd in de berekening geen rol speelt, en alleen quantummechanica is daarom genoeg om een vrijwel exact antwoord te krijgen. Aan de andere kant is bijvoorbeeld voor het bepalen van de baan van een komeet het precieze quantummechanische gedrag van de deeltjes waaruit de komeet is opgebouwd verwaarloosbaar. Een plek waar beide theorieën niet verwaarloosbaar zijn, is in de buurt van een zwart gat. Bij de vorming van een zwart gat komen heel veel deeltjes samen in een heel kleine ruimte, waardoor quantummechanische effecten belangrijk worden. De deeltjes die het zwarte gat gevormd hebben zijn bij elkaar echter ook enorm zwaar, waardoor ze de ruimtetijd beïnvloeden en algemene relativiteit van belang is.

Om deze situatie toch te kunnen beschrijven wordt er gezocht naar een overkoepelende theorie, die de naam ‘quantumzwaartekracht’ heeft gekregen. Deze term heeft voor verschillende mensen verschillende betekenissen. Voor sommigen betekent het ‘een quantumtheorie van zwaartekracht’, wat wil zeggen dat algemene relativiteit een quantumtheorie wordt. Voor anderen betekent het iets breders, namelijk ‘een theorie die zowel quantummechanica als algemene relativititeit beschrijft’. Er zijn verschillende aanpakken voor de zoektocht naar quantumzwaartekracht. Het bekendste voorbeeld is waarschijnlijk snaartheorie, een theorie die op deze website al regelmatig aan bod is gekomen. Dat is ook niet zo gek: de Quantum Universe-website is oorspronkelijk opgezet met hulp van de Spinozapremie die snaartheoreet Erik Verlinde won, en veel redactieleden zijn nog steeds uit de snaartheoriegroep afkomstig. Ik zal de snaartheorie-aanpak, maar zeker ook andere aanpakken, kort toelichten.
Snaartheorie is de populairste en verst ontwikkelde aanpak voor quantumzwaartekracht. Snaartheorie is van quantummechanische aard en beschrijft deeltjes als minuscule snaren in plaats van als puntvormige objecten. Al snel in de ontwikkeling werd duidelijk dat zo’n beschrijving wiskundig alleen consistent gemaakt kan worden wanneer de theorie wordt beschreven in een ruimtetijd met tien dimensies. Dit betekent dat, om onze wereld te beschrijven, de theorie op de een of andere manier moet worden gereduceerd tot een model van vier dimensies. Dat kan op veel verschillende manieren worden gedaan. De resultaten van die verschillende reducties worden ‘vacua’ genoemd. Daar zijn er heel veel van, en bovendien zijn er verschillende manieren om de theorie op te zetten, wat nog meer vacua oplevert. Het is nog onduidelijk of er een vacuüm is dat ons universum beschrijft, en hoe dat dan kan worden gevonden. De best begrepen manier om aan snaartheorie te rekenen is perturbatief, wat wil zeggen dat de uitkomsten van berekeningen stap voor stap worden bepaald: eerst wordt een grove benadering gemaakt en vervolgens worden correcties op die benadering berekend. Over niet-perturbatieve beschrijvingen van snaartheorie is veel minder bekend, behalve in enkele specifieke gevallen van de AdS/CFT-correspondentie. Sommige snaartheoreten benadrukken dit door te zeggen dat er nog geen sprake is van ‘snaartheorie’, maar alleen van ‘perturbatieve snaartheorie’.
Lusquantumzwaartekracht is een aanpak waarin de meetkunde van de ruimtetijd, die in Einsteins algemene relativiteit het belangrijkste bestanddeel vormt, wordt vervangen door een quantummeetkunde. Het uitgangspunt van deze aanpak is om de zwaartekracht én andere natuurkrachten te formuleren op een manier die niet afhankelijk is van de achtergrond. Dit betekent dat de vergelijkingen van de theorie geen specifieke ruimtetijd of deeltjesvelden als invoer vereisen. Om een quantummeetkunde te maken, wordt gebruik gemaakt van bepaalde lussen, wat de naam van de aanpak verklaart. Deze lussen moeten niet worden verward met de snaren uit snaartheorie, ze beschrijven namelijk de ruimtetijd zélf, in plaats van deeltjes die door de ruimtetijd heen bewegen. De dynamica kan worden beschreven met Hamiltoniaanse methodes, of via een achtergrond-onafhankelijke formulering van padintegraaltechnieken, die bekendstaat onder de naam ‘spin foams’. Voor lusquantumzwaartekracht bestaan nog belangrijke open vragen op fundamenteel niveau, die verder onderzoek vereisen1.
Asymptotische veiligheid is quantumtheoretisch van aard en geeft een voltooiing of uitbreiding van een effectieve veldentheorie in het hoog-energetische regime. Dat wil zeggen dat de aanpak ervan uitgaat dat een theorie die geldig is bij lage energieën (zoals algemene relativiteit of quantummechanica) kan worden uitgebreid naar steeds hogere energieën. De aanpak is gebaseerd op ideeën uit de statistische fysica en maakt gebruik van renormalisatietechnieken uit de quantumveldentheorie. De theorie is minimalistisch in de zin dat ze geen radicale nieuwe ideeën over de quantumaard van de ruimtetijd vereist. De meeste resultaten zijn echter verkregen voor berekeningen aan een Euclidische ruimtetijd (waarin tijd en ruimte dezelfde rol spelen), en het blijkt vooralsnog moeilijk om deze om te zetten naar een Lorentzische ruimtetijd (waarin tijd en ruimte een andere rol hebben), terwijl ons universum van deze laatste soort is2.
Causale dynamische triangulaties vormen een niet-perturbatieve aanpak voor quantumzwaartekracht die gebruikmaakt van padintegralen. In deze aanpak wordt gesommeerd over alle mogelijke triangulaties van de ruimtetijd waarbij een tijd-oriëntatie aanwezig is. Een triangulatie is een opdeling in driehoekjes, waarna alles wordt vergeten behalve de punten van de driehoeken en de lijnen tussen die punten – wat overblijft heet een rooster. Vervolgens wordt er gezocht naar een limiet waarin de grootte van de lijnen in het rooster naar nul gaat, om zo een theorie van een volledige ruimtetijd te krijgen. Vanwege de som over triangulaties is de limiet niet afhankelijk van een vaste achtergrond. Er zijn allerlei numerieke technieken beschikbaar voor deze methode, maar er zijn nog belangrijke fundamentele vragen die meer onderzoek vereisen3.

Causale verzamelingen vormen de basis van een aanpak die ervan uitgaat dat ruimtetijd fundamenteel discreet is: uit ondeelbare bouwstenen bestaat, in plaats van continu en Lorentzisch te zijn. Zo’n causale verzameling kan bijvoorbeeld worden verkregen door willekeurig punten uit een Lorentzische ruimtetijd te bekijken, maar niet elke causale verzameling wordt op deze manier verkregen. Daardoor heeft ook niet elke causale verzameling een continue limiet. De dynamica in de theorie benadert de dynamica van de algemene relativiteitstheorie. Maar dat is nog niet geheel geruststellend: het is onder meer lastig om onderscheid te maken tussen fysisch realistische en fysisch onrealistische causale verzamelingen4.
Niet-commutatieve meetkunde is wellicht meer ontwikkeld als wiskundige theorie dan als aanpak voor quantumzwaartekracht. In niet-commutatieve meetkunde wordt de Hilbertruimte-formulering van quantummechanica als fundamenteel beschouwd. Algemene relativiteit wordt vervolgens ook beschreven in termen van een Hilbertruimte door de meetkunde van ruimtetijd uit te drukken in een zogenaamd spectraaltripel. Dynamica zou dan worden beschreven door een padintegraal over spectraaltripels. Ook voor deze aanpak geldt dat er nog veel fundamentele open vraagstukken zijn. Het is bijvoorbeeld nog onduidelijk wat precies een spectraaltripel voor een Lorentzische oneindig uitgestrekte ruimtetijd moet zijn. De niet-commutatieve meetkunde is toevallig de onderzoeksrichting binnen de wiskunde waar mijn eigen onderzoek onder valt: daarbij probeer ik de wiskunde achter niet-commutatieve meetkunde te combineren met ideeën uit de snaartheorie.
Er zijn nog meer aanpakken van quantumzwaartekracht, met namen als “Hořava-Lifschitzzwaartekracht”, “twistortheorie” of “Reggecalculus”, dus bovenstaande lijst is niet uitputtend. Ook staan de verschillende aanpakken niet allemaal los van elkaar. Zo liggen ideeën van asymptotische veiligheid aan de basis van causale dynamische triangulaties, en vormt volgens sommige natuurkundigen niet-commutatieve meetkunde een deel van snaartheorie. Het hoeft dus ook zeker niet het geval te zijn dat precies één van deze aanpakken het uiteindelijke antwoord gaat zijn: misschien moeten ideeën uit de verschillende aanpakken worden gecombineerd, of misschien moet er wel iets heel nieuws worden bedacht.

Voor natuurkundigen die werken aan quantumzwaartekracht is het al lastig om op de hoogte te blijven van de ontwikkelingen binnen hun eigen aanpak, laat staan van ontwikkelingen in de andere aanpakken. Mede daarom schreef Jay Armas een boek waarin hij 37 vooraanstaande onderzoekers interviewde die werken aan verschillende aanpakken voor quantumzwaartekracht. In deze interviews werd bijvoorbeeld gevraagd naar de status van hun onderzoeksgebied en hun visie op quantumzwaartekracht. Voor een artikel dat binnenkort op deze website verschijnt, zijn de rollen omgedraaid en heb ik Jay Armas geïnterviewd. Het bovenstaande overzicht van de verschillende aanpakken biedt een korte inleiding in het probleem van quantumzwaartekracht, en dient daarmee als proloog voor het interview met Jay Armas. Hou deze website in de gaten voor het interview zelf!
[1] De bron voor de samenvatting van lusquantumzwaartekracht is dit artikel.
[2] De bron voor de samenvatting van asymptotische veiligheid is dit artikel.
[3] De bron voor de samenvatting van causale dynamische triangulaties is dit artikel.
[4] De bron voor de samenvatting van causale verzamelingen is dit artikel.