
Een type vraag die regelmatig op bijvoorbeeld een IQ-test verschijnt is het aanvullen van een getallenreeks. Een voorbeeld hiervan is een reeks zoals 1, 2, 4, 8, 16, … De vraag is dan om te raden wat het volgende getal is. In dit voorbeeld herken je waarschijnlijk de machten van twee, en dus is het een redelijke aanname dat het volgende getal in de reeks 32 is.
De natuurkunde zit vol met getallenreeksen, en het is daarom ook nuttig om dit soort patronen te herkennen. Die stellen je in staat om het onderliggende probleem beter te begrijpen en tot nieuwe inzichten te komen. Een zeker patroon kan mogelijk wijzen op een symmetrie van het onderliggende model, wat ons weer in staat stelt om makkelijker een oplossing te vinden. Voor de natuurkundige staat wiskunde vooral in dienst van het tot stand komen van nieuwe fysische inzichten, en bij het zien van zo’n patroon zal een natuurkundige dan ook al snel redeneren:
If it looks like a duck, swims like a duck, and quacks like a duck, then it probably is a duck.
Wiskundigen zijn echter niet zo happig op zo’n snelle conclusie en willen eerst een formeel bewijs zien dat aantoont dat het waargenomen patroon ook echt van toepassing is. Daar zijn goede redenen voor, omdat er altijd de kans bestaat dat het patroon incorrect is. Het volgende getal in de getallenreeks hierboven zou ook iets heel anders dan 32 kunnen zijn – wellicht gaat het wel om de verjaardagen van de eerste Nobelprijswinnaars in de natuurkunde, en vielen die toevallig op die dagen van de maand. Er is natuurlijk altijd een goede kans dat onze intuïtie correct is, maar er zijn ook voorbeelden die je intuïtie kunnen misleiden.
Het cirkelprobleem van Moser
Het eerste voorbeeld is het cirkelprobleem van Moser – vernoemd naar de wiskundige Leo Moser. Het probleem gaat over het bepalen van het aantal vlakken waarin een cirkel wordt opgedeeld als we \( n \) punten op de rand plaatsen en die allemaal verbinden met rechte lijnen. Om dit te illustreren beginnen we dus met een grote ronde cirkel waarop we één punt plaatsen. Aangezien dit nog het enige punt is, zijn er geen lijnen te trekken en dus is er slechts één vlak, namelijk de gevulde cirkel zelf. Als we dan een tweede punt op een willekeurige plek langs de rand plaatsen, en vervolgens een lijn trekken tussen de twee punten, dan wordt de cirkel in twee vlakken gedeeld. Met twee punten op de rand kunnen we de cirkel dus in twee vlakken opdelen. Nu plaatsen we een derde punt op een wederom willekeurige plek op de rand van de cirkel, en trekken we twee lijnen van dit nieuwe punt naar de eerste twee punten. Nu vormen de lijnen een driehoek die de cirkel opdelen in vier vlakken. Als we dan een vierde punt plaatsen, wat leidt tot drie nieuwe lijnen, vinden we een cirkel opgedeeld in acht vlakken en als we dit nogmaals doen met een vijfde punt vinden we zestien vlakken. Zie je al het patroon?
Het is vrij redelijk om aan te nemen dat de getallen in de reeks van de vorm \( 2^{n-1} \) zijn – waarbij \( n \) het aantal punten op de cirkel is – wat min of meer dezelfde reeks is die ik in de introductie beschreef. Het is dus ook niet gek om te denken dat we na het toevoegen van een zesde punt \( 2^5 = 32 \) vlakken vinden. Dit is echter niet het geval! Als je een zesde punt toevoegt en de nieuwe lijnen trekt, vind je dat de cirkel wordt opgedeeld in niet 32, maar 31 vlakken!
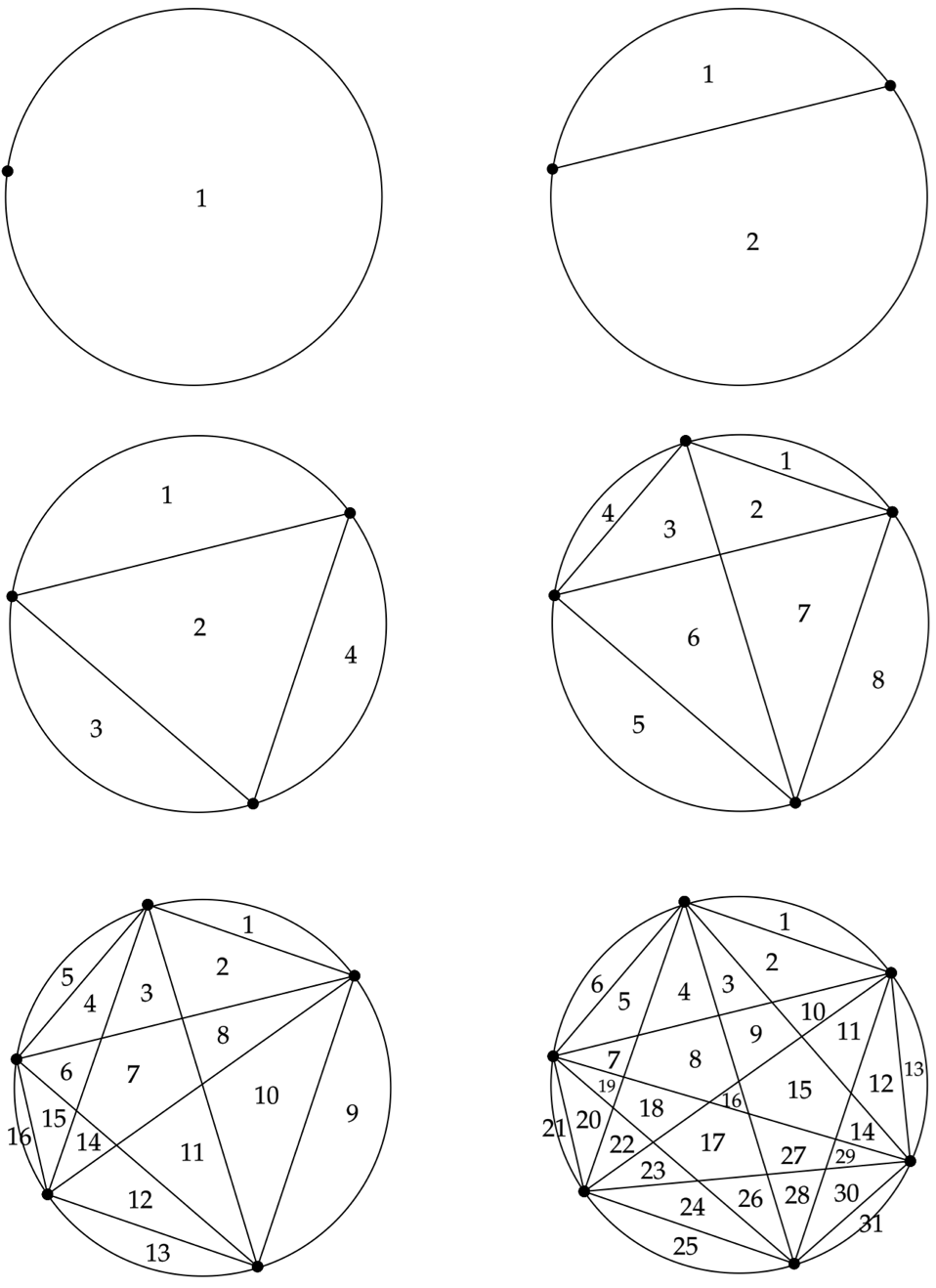
Het patroon \( 2^{n-1} \) dat we meenden waar te nemen is dus incorrect. De correcte formule voor het aantal vlakken, laten we dat \( m \) noemen, kun je wel degelijk in gesloten vorm vinden. Dat aantal wordt beschreven door1
\( m = {n \choose 4} + {n \choose 2} + 1 \).
Je kunt narekenen dat dit de reeks 1, 2, 4, 8, 16, 31, 57, 99, … geeft, en concluderen dat de eerste vijf coëfficiënten ons dus op het verkeerde been hebben gezet!
Nu zou je kunnen beargumenteren dat het ook wel erg naïef is om na vijf getallen al te denken dat je het hele patroon doorhebt, en dat je pas vanaf tien of twintig voorbeelden met zekerheid een constatering kan maken. Er zijn echter voorbeelden van incorrecte waarnemingen die heel veel langer standhouden. Eén daarvan is de structuur van zogenaamde cyclotomische polynomen.
Het ontbinden van polynomen
Cyclotomische polynomen verschijnen wanneer we het ogenschijnlijk eenvoudige polynoom
\( x^n-1 \),
proberen te ontbinden in polynomen van lagere graad, voor willekeurige positieve gehele getallen \( n \). Met graad bedoelen we de hoogste macht van \( x \) in het polynoom, wat in het bovenstaande voorbeeld altijd \( n \) is. Neem als voorbeeld de ontbinding van dit polynoom voor \( n=6 \), wat leidt tot
\( x^6-1 = (x^2-x+1)(x^2+x+1)(x+1) (x-1) \).
We hebben hier een zesdegraads polynoom ontbonden in vier nieuwe polynomen, waarvan er twee tweedegraads en twee eerstegraads zijn. De tweedegraads polynomen zou je eventueel nog kunnen ontbinden als het product van twee eerstegraads polynomen, maar in dat geval moet je met complexe getallen werken; die zullen we in dit probleem vermijden. We noemen een polynoom dat niet langer ontbonden kan worden – ofwel omdat die eerstegraads is, ofwel omdat we dan complexe getallen krijgen – een onherleidbaar polynoom.
Laten we eens kijken naar de ontbinding van de polynomen \( x^n-1 \) in termen van zulke onherleidbare polynomen. Voor de eerste acht vinden we
\( \begin{eqnarray} x^1-1 & = & x-1 \\ x^2-1 & = & (x+1) \, (x-1) \\ x^3-1 & = & (x^2+x+1) \, (x-1) \\ x^4-1 & = & (x^2+1) \, (x+1) \, (x-1) \\ x^5-1 & = & (x^4+x^3+x^2+x+1) \, (x-1) \\ x^6-1 & = & (x^2-x+1) \, (x^2+x+1) \, (x+1) \, (x-1) \\ x^7-1 & = & (x^6+x^5+x^4+x^3+x^2+x+1) \, (x-1) \\ x^8-1 & = & (x^4+1) \, (x^2+1) \, (x+1) \, (x-1) \end{eqnarray} \).
Als je maar lang genoeg deze polynomen bestudeert, dan valt het volgende op: alle polynomen zijn deelbaar door het polynoom \( (x-1) \), want dat verschijnt iedere keer aan de rechterzijde. We noemen dit polynoom \( \Phi_1(x) = x-1 \) het eerste cyclotomische polynoom. Daarna is er het tweede cyclotomische polynoom \( \Phi_2(x) = x+1 \) dat alle polynomen deelt waarvoor \( n \) even is. Als je goed kijkt vind je dat bij iedere hogere \( n \) een nieuw polynoom aan de rechterzijde verschijnt dat we nog niet eerder gezien hebben en dat we kunnen identificeren als het \( n \)-de cyclotomische polynoom \( \Phi_n(x) \). We kunnen dan de bovenstaande ontbindingen herschrijven als
\( \begin{eqnarray} x^1-1 & = & \Phi_1(x) \\ x^2-1 & = & \Phi_2(x) \, \Phi_1(x) \\ x^3-1 & = & \Phi_3(x) \, \Phi_1(x) \\ x^4-1 & = & \Phi_4(x) \, \Phi_2(x) \, \Phi_1(x) \\ x^5-1 & = & \Phi_5(x) \, \Phi_1(x) \\ x^6-1 & = & \Phi_6(x) \, \Phi_3(x) \, \Phi_2(x) \, \Phi_1(x) \\ x^7-1 & = & \Phi_7(x) \, \Phi_1(x) \\ x^8-1 & = & \Phi_8(x) \, \Phi_4(x) \, \Phi_2(x) \, \Phi_1(x) \end{eqnarray} \).
Een bijzondere eigenschap die we dan vinden, is dat het polynoom \( x^n-1 \) altijd te ontbinden is in termen van cyclotomische polynomen waarvan het label een deler van \( n \) is! Maak je geen zorgen: dit is geen valstrik zoals in het vorige voorbeeld, maar een echte eigenschap die tot alle hogere ordes standhoudt.
Als we de cyclotomische polynomen zelf echter nog eens uitschrijven, dan valt er nog iets anders op:
\( \begin{eqnarray} \Phi_1 & = & x-1 \\ \Phi_2 & = & x+1 \\ \Phi_3 & = & x^2+x+1 \\ \Phi_4 & = & x^2+1 \\ \Phi_5 & = & x^4+x^3+x^2+x+1 \\ \Phi_6 & = & x^2-x+1 \\ \Phi_7 & = & x^6+x^5+x^4+x^3+x^2+x+1 \\ \Phi_8 & = & x^4+1 \end{eqnarray} \).
Alle coëfficiënten van de polynomen zijn 1 of -1. Je kunt nog honderd ordes in \( n \) uitrekenen, maar dit patroon zal standhouden. Voor de 99ste en 100ste cyclotomische polynomen vinden we bijvoorbeeld
\( \begin{eqnarray} \Phi_{99}(x) & = & x^{60}-x^{57}+x^{51}-x^{48}+x^{42}-x^{39}+x^{33}-x^{30}+x^{27} \\ && \qquad -x^{21}+x^{18}-x^{12}+x^{9}-x^{3}+1 \\ \Phi_{100}(x) & = & x^{40}-x^{30}+x^{20}-x^{10} + 1 \end{eqnarray} \).
Menig natuurkundige zou op dit moment deze observatie voor algemene wetmatigheid aanzien en accepteren dat alle coëfficiënten in alle cyclotomische polynomen 1 of -1 moeten zijn. Als we nog net iets verder kijken, zien we echter een breuk in deze trend. Aangekomen bij het 105de polynoom, vinden we namelijk
\( \begin{eqnarray} \Phi_{105} & = & x^{48}+x^{47}+x^{46}-x^{43}-x^{42}-2 x^{41}-x^{40}-x^{39}+x^{36}+x^{35}+x^{34} \\ && \quad +x^{33}+x^{32}+x^{31}-x^{28}-x^{26}-x^{24}-x^{22}-x^{20}+x^{17}+x^{16} \\ && \quad +x^{15}+x^{14}+x^{13}+x^{12}-x^9-x^8-2x^7-x^6-x^5+x^2+x+1 \end{eqnarray} \).
Er verschijnen termen \( -2x^{41} \) en \( -2x^7 \) in het polynoom! Het patroon dat we dus voor de eerste 104 ordes meenden te herkennen is tóch incorrect. Dit toont aan waarom het netjes bewijzen van een wiskundige stelling zo belangrijk is: men kan nog zoveel voorbeelden vinden waarin een vermoeden lijkt te kloppen; zonder bewijs is er geen enkele garantie dat er niet een tegenvoorbeeld bestaat. Dit geldt ook voor enkele wereldberoemde problemen zoals de Riemannhypothese en het vermoeden van Collatz. Hoewel we (met behulp van computers) al miljoenen voorbeelden van die vermoedens hebben kunnen natrekken, die allemaal voldoen aan deze hypotheses, blijft de mogelijkheid bestaan dat er op een zeker moment een tegenvoorbeeld verschijnt, net zoals we hier zien met het 105de cyclotomische polynoom. Vertrouw in de wis- en natuurkunde dus nooit té veel op je intuïtie!
[1] Als je benieuwd bent hoe deze uitdrukking tot stand komt, raden we je aan deze video van 3Blue1Brown op YouTube te kijken.