Afbeelding 1. Turks schaaltje.
De afbeelding op dit Turkse schaaltje is spiegel- en rotatiesymmetrisch. Afbeelding: wikipedia-gebruiker Dmharvey
In de natuurkunde zijn symmetrieën heel belangrijk. Ze vormen vaak de basis voor een versimpeling van het probleem en hebben verregaande gevolgen. Voor velen is symmetrie een vanzelfsprekend begrip. Onze hersenen zijn namelijk goed in het herkennen van patronen, en we kunnen snel beoordelen wanneer iets symmetrisch is of niet. Zonder na te denken zie je immers dat het Turkse schaaltje hieronder symmetrisch is.
In deze serie zullen we uitleggen waarom symmetrieën een van de fundamenten – zo niet hét fundament – van de natuurkunde zijn. In het eerste deel zullen we het begrip symmetrie beter bestuderen en een beetje in de wiskunde duiken. In het tweede deel zullen we meer naar de natuurkunde kijken. We zullen ons daar focussen op een concreet voorbeeld waar symmetrieën belangrijk zijn, namelijk ons zonnestelsel. In ons zonnestelsel draaien de planeten in een stabiele baan rond de zon en vallen niet naar de zon, ondanks het feit dat zwaartekracht een aantrekkende kracht is. Om dit te kunnen verklaren hebben we symmetrieën nodig. Volgende keer zullen we bespreken hoe symmetrieën er precies voor zorgen dat de planeten op hun plek blijven!
Wat is een symmetrie?
Theoretisch gezien is een symmetrie een transformatie van een object die het object onveranderd laat. Dit is een moeilijke zin, dus laten we hem toelichten door middel van twee voorbeelden.
Ten eerste bekijken we een vierkant. Dit vierkant kunnen we rondom het middelpunt over een hoek van 90 graden draaien zonder dat het vierkant verandert. Maar ook als je een spiegel op een diagonaal van het vierkant zet, blijft het vierkant hetzelfde als je in de spiegel kijkt. De transformaties zijn in dit geval een rotatie over 90 graden en de spiegelingen in de diagonaal; het vierkant is het object.
Een ander voorbeeld is een lolly. Als je het stokje van de lolly draait, dan verandert de lolly niet. Bovendien kun je het stokje verticaal, horizontaal of onder een hoek houden; telkens als je het stokje draait blijft de lolly hetzelfde. Dit komt doordat de lolly een bol is en een bol verandert niet als je hem draait. In dit voorbeeld zijn de transformaties willekeurige rotaties; het object is de bolvormige lolly.
Afbeelding 2. Lolly.
Een lolly is rotatiesymmetrisch.
De symmetrieën van een vierkant
In de wiskunde zijn de transformaties die we hierboven beschreven hebben erg belangrijk. In de voorbeelden hierboven hebben een aantal voorbeelden van symmetrieën genoemd, maar wiskundig is het veel interessanter om tegelijkertijd te kijken naar alle symmetrieën van een voorwerp. Laten we het vierkant nog eens wat beter bekijken. We willen alle mogelijke transformaties van het vierkant vinden en kijken wat de structuur daarvan is.
Naast de rotatie van 90 graden hebben we natuurlijk ook rotaties over hoeken van 180, 270 en 360 graden. De laatste is in zekere zin bijzonder, want die doet niks met het vierkant en is gelijk aan een rotatie van nul graden. De overige rotaties kun je ook verkrijgen door het vierkant 2 of 3 keer over een hoek van 90 graden te draaien. Dus de rotatie van 90 graden is voldoende om alle andere transformaties (althans de rotaties) te genereren. We noemen een rotatie over 90 graden R. Nu we weten hoe rotaties werken, zullen we de spiegelingen bestuderen.
Hieronder zie je een afbeelding van een vierkant. De hoekpunten hebben we genummerd om de rotaties en spiegelingen te verduidelijken. De rode lijn geeft de spiegel aan. Als we nu het vierkant in de rode lijn spiegelen – deze transformatie noemen we S – dan worden hoekpunten 2 en 4 verwisseld. Dit is niet de enige spiegeling; er zijn er meer. In de onderste twee vierkanten zie je een verticale spiegeling, die de hoekpunten 3 en 4, en 1 en 2 verwisselt – deze transformatie noemen we S’. Deze transformatie kunnen we echter ook nog op een andere manier verkrijgen, namelijk door het tweede vierkant in de bovenste rij één keer over 90 graden te draaien (transformatie R). Dus hieruit volgt de vergelijking
S′ = R·S
Transformaties worden in de wiskunde van rechts naar links gelezen. Omdat S eerst wordt toegepast, staat deze dus het meest rechts. De punt is een vermenigvuldigingspunt; het blijkt in de wiskunde erg nuttig te zijn om over het na elkaar toepassen van transformaties te denken als het ‘vermenigvuldigen’ van transformaties. Zo kunnen we twee keer achter elkaar uitvoeren van R bijvoorbeeld schrijven als R2.
Natuurlijk zijn er nog twee spiegelingen. Ga zelf na dat deze gegeven worden door een keer te spiegelen en twee keer of drie keer te draaien. Dit noteren we met R2·S en R3·S, waarbij de macht weer voor het aantal maal draaien staat.
Nu hebben we alle transformaties die het vierkant onveranderd laten gevonden! Dit zijn:
R, R2, R3, R4, S, R·S, R2·S, R3·S
en niet meer! Neem bijvoorbeeld een rotatie over 540 graden, dus zes keer draaien. Als je van de zes keer draaien er vier toegepast hebt, dan ben je weer terug bij af en dus doen die vier er niet toe. De overige twee keer draaien is wat er daadwerkelijk toe doet. Een rotatie over 540 graden is dus gelijk over een hoek van 180 graden. Ook al bedenk je de meest waanzinnige symmetrietranformatie (die het vierkant onveranderd laat), deze is altijd gelijk aan een van de bovenstaande 8 transformaties.
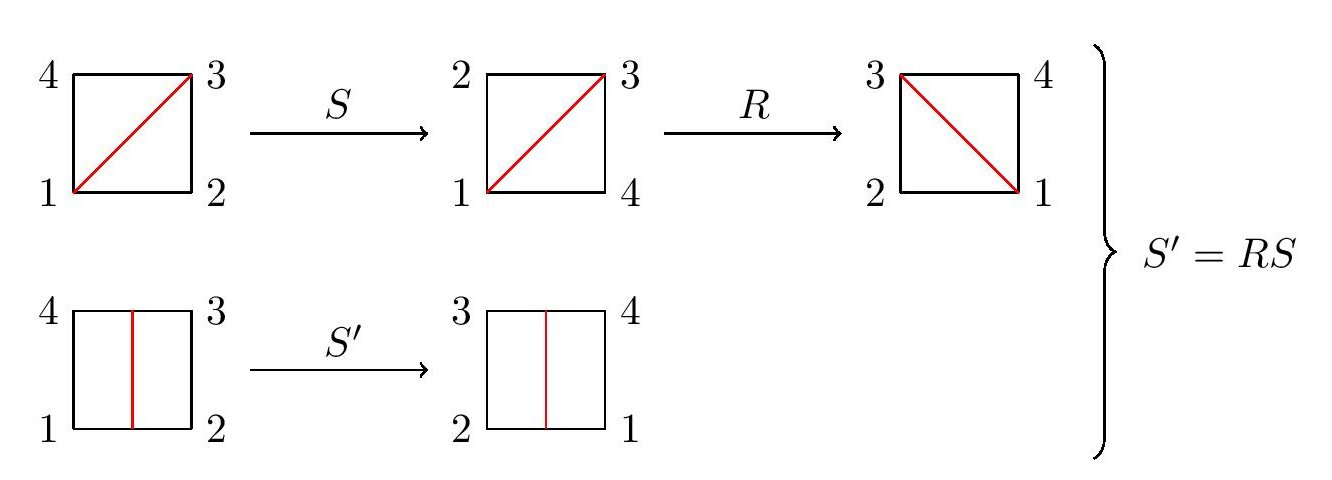
Afbeelding 3. Symmetrieën van een vierkant.Je ziet hier twee symmetrietransformaties van het vierkant, die hetzelfde blijken te zijn. De bovenste transformatie bestaat uit een keer spiegelen in de diagonaal (S) en een keer draaien onder een hoek van 90 graden (R). De onderstaande transformatie is een spiegeling in een verticale lijn (S’).
Groepen
In de wiskunde noemen we de verzameling van symmetrietranformaties, zoals hierboven, een groep. Het feit dat elke symmetrietransformatie één van de bovenstaande 8 is, is een eigenschap van een groep. Deze eigenschap wordt geslotenheid genoemd. Daarnaast zijn er nog andere eigenschappen die wiskundigen aan een verzameling toekennen voordat je haar een groep mag noemen. Ten eerste moet een groep een transformatie bevatten die niets doet. In het geval van het vierkant is dat R4, want dat is hetzelfde als een rotatie over nul graden. Dit element wordt het eenheidselement genoemd en wordt met e aangeduid. Ten tweede bestaat er voor elk element van de groep een inverse. Dit is een element die de transformatie weer ongedaan maakt. Bijvoorbeeld: een rotatie over 90 graden kun je ongedaan maken door het vierkant nog eens 270 graden te draaien, want dan ben je weer terug bij af. Voor een spiegeling S is dat natuurlijk de spiegeling zelf. In formules geven we dit als volgt weer:
R3·R = e, S·S = e.
Een groep is niet alleen een belangrijke structuur in de wiskunde, maar ook in de theoretische natuurkunde. In bijna alle vakgebieden van de theoretische natuurkunde wordt er volop gebruik van gemaakt. In het volgende artikel zullen we kijken waarom een dergelijke structuur belangrijk is voor ons zonnestelsel.

