
Een van de bekendste resultaten uit de wiskunde is de stelling van Pythagoras. Deze stelling geeft een manier om de schuine zijde van een driehoek met één hoek van 90 graden uit te drukken in termen van de andere zijdes. In formulevorm:
\( a^2+b^2=c^2 \).
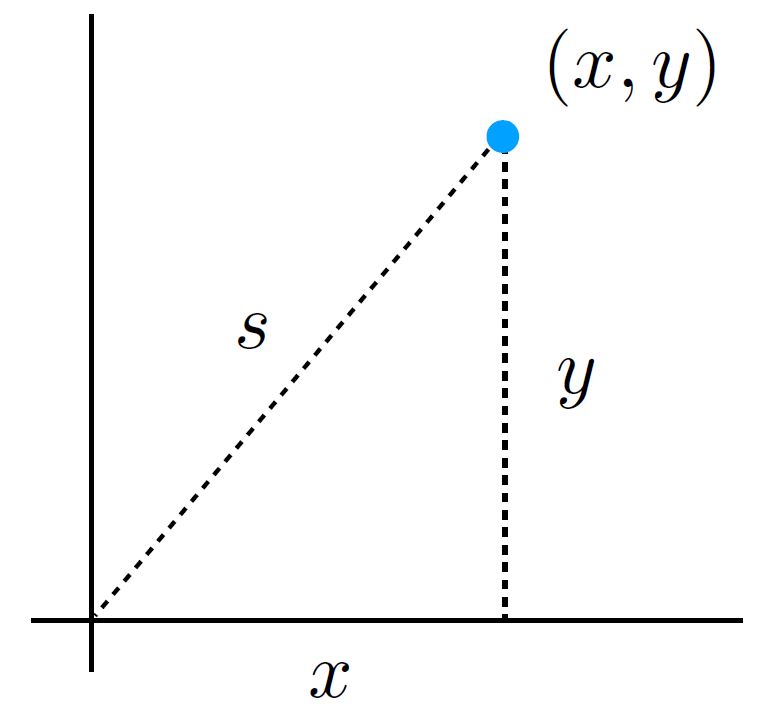
De letters \( a, b \) en \( c \) staan voor de lengtes van de zijden van de driehoek, waarbij \( c \) de lengte van de schuine zijde is. Een belangrijke toepassing van de stelling is dat je er afstanden mee kunt uitrekenen. Hoe bereken je de afstand tot de oorsprong van een punt met coördinaten \( (x,y) \)? Door een driehoek te teken waarvan de schuine zijde de oorsprong met het punt \( (x,y) \) verbindt (zie afbeelding 2), komen we uit op de volgende formule voor de afstand \( s \):
\( s^2 = x^2 + y^2 \).
Door vervolgens de wortel te nemen aan beide kanten vinden we de gebruikelijke afstandsformule voor \( s \). Kunnen we een soortgelijke vergelijking gebruiken om afstanden te berekenen tussen gebeurtenissen in de ruimtetijd?
Aan het begin van de vorige eeuw – in 1905, om precies te zijn – vond er een revolutie plaats in de natuurkunde die begon toen Albert Einstein zijn speciale relativiteitstheorie presenteerde. Relativiteitstheorie is een uitgebreid onderwerp waar je meerdere artikelen over kunt vullen; zie bijvoorbeeld deze reeks artikelen voor een uitgebreidere uitleg. Hier zal ik in vogelvlucht de belangrijkste onderdelen herhalen. Einsteins theorie is gebaseerd op twee aannames:
- De natuurwetten zijn gelijk voor waarnemers die met een constante snelheid ten opzichte van elkaar bewegen.
- De lichtsnelheid heeft dezelfde waarde \( c \) voor waarnemers die met een constante snelheid ten opzichte van elkaar bewegen.
De eerste aanname is eigenlijk niet zo gek, en was in feite al geaccepteerd voordat Einstein met zijn theorie kwam. Stel je voor dat je in een trein zit die met hoge constante snelheid beweegt. Kun je dan iets doen om zonder informatie van buitenaf (dus je mag bijvoorbeeld niet uit het raampje kijken) erachter te komen dat je in beweging bent? De eerste aanname zegt precies dat dit niet mogelijk is: je merkt er niks van dat je in beweging bent. Vanuit jouw perspectief staat de trein stil, en beweegt de rest van de wereld in tegengestelde richting. Zodra de trein afremt of versnelt, merk je pas dat je daadwerkelijk beweegt – omdat je kop koffie bijvoorbeeld omvalt.
De tweede aanname hierboven is een stuk vreemder en druist volledig in tegen de manier waarop we normaal gesproken met snelheden rekenen. Bijvoorbeeld: als ik naar een rijdende auto – zeg met een snelheid van 50 km/u – toe beweeg met een snelheid van 5 km/u lijkt de snelheid van de auto vanuit mij gezien hoger dan de snelheid die ik vanuit stilstand waarneem – namelijk de som van beide snelheden 50 + 5 = 55 km/u. Voor licht blijkt dit niet het geval! Met welke snelheid je ook ten opzichte van de lichtbron beweegt, je meet altijd dezelfde lichtsnelheid.
Om aan beide aannames te voldoen kwam Einstein tot de volgende vérstrekkende conclusie: ruimte en tijd staan niet lost van elkaar, maar vormen een geheel dat we ruimtetijd noemen. Een ‘punt’ in de ruimtetijd is een gebeurtenis die op een bepaalde plek en tijd plaatsvindt. Er zijn drie ruimtelijke dimensies. We hebben namelijk drie coördinaten nodig om een punt in de ruimte aan te geven. Als we tijd meetellen is de ruimtetijd daarmee vierdimensionaal. Hoe meten we de afstand tussen twee gebeurtenissen in deze vierdimensionale ruimtetijd?
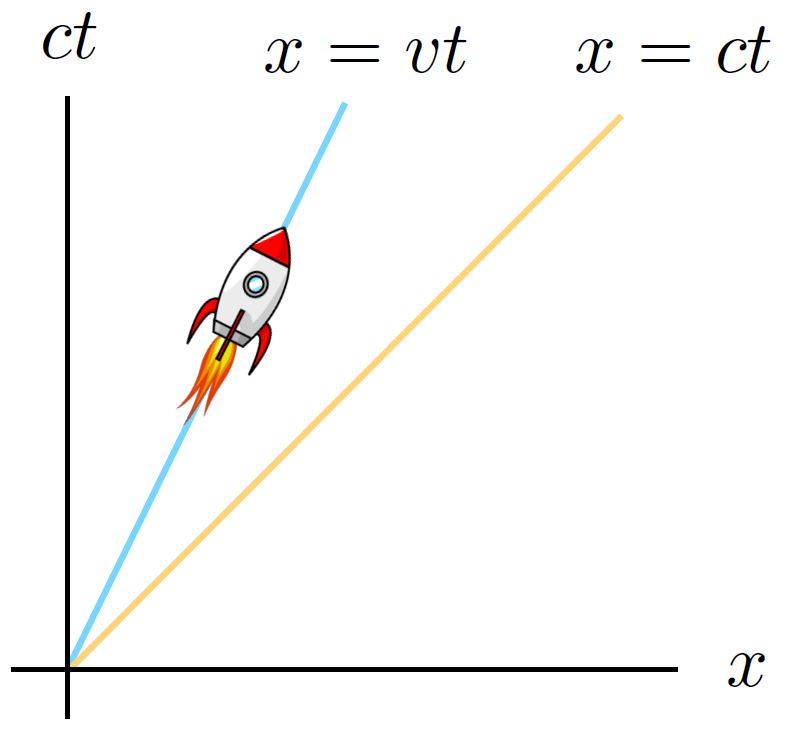
Laten we voor het gemak aannemen dat we maar één ruimtelijke dimensie hebben in plaats van drie; we vergeten dus even twee dimensies. We kunnen de ruimtetijd dan weergeven als een tweedimensionaal vlak met een ruimtelijke coördinaat in de horizontale richting en een tijdscoördinaat in de verticale richting (zie afbeelding 3). We vermenigvuldigen de tijdscoördinaat \( t \) met de lichtsnelheid \( c \), zodat deze coördinaat ook de eenheden heeft van een afstand: snelheid maal tijd is immers afstand. Door de tijd op deze manier te herschalen maakt een lichtstraal (de gele lijn in afbeelding 3) altijd een hoek van 45 graden met de verticale as. Wat is de afstand tussen een punt \( (x,ct) \) in het ruimtetijdvlak en de oorsprong? Dat hangt natuurlijk af van wat je precies met ‘afstand’ bedoelt. Het belangrijke inzicht van Einstein was dat de nuttigste afstandsmaat er iets anders uitziet dan de stelling van Pythagoras die we voor de ruimtelijke dimensies gebruiken. Hij stelde voor dat we een afstand kunnen definiëren door het volgende experiment uit te voeren. We geven een klok mee aan een waarnemer die met constante snelheid vanuit de oorsprong naar het ruimtetijdpunt in kwestie beweegt. De verlopen tijd op de klok bij aankomst noemen we de eigentijd van de waarnemer, en dat blijkt een geschikte ‘afstandsmaat’ op de ruimtetijd te zijn.
Om een formule voor de eigentijd af te leiden doen we een gedachte-experiment. Het bijhorende ruimtetijdplaatje is weergeven in afbeelding 4. We nemen aan dat we twee waarnemers hebben (aangegeven met rood en blauw) die beide in de oorsprong beginnen. Daar maken ze de volgende afspraak. Een van de waarnemers vertrekt met een constante snelheid in een bepaalde richting. Hij neemt een klok mee om de tijd bij te houden. Kort daarna stuurt de andere waarnemer – die in stilstand blijft ten opzichte van het originele coördinatensysteem – een lichtsignaal in de richting van de bewegende waarnemer. Het ontvangen van het lichtsignaal is nu de gebeurtenis waarvan we de eigentijd willen uitrekenen. Beide waarnemers noteren het tijdstip dat de bewegende waarnemer het lichtsignaal ontvangt. Vanuit de stilstaande waarnemer (rood) gebeurt dit op tijd \( t \), maar vanuit de bewegende waarnemer (blauw) gebeurt dit op een tijdstip \( \tau \), de eigentijd. Direct nadat hij het lichtsignaal heeft ontvangen stuurt de bewegende waarnemer een lichtsignaal terug. Dit signaal komt een tijdje later aan bij de stilstaande waarnemer.
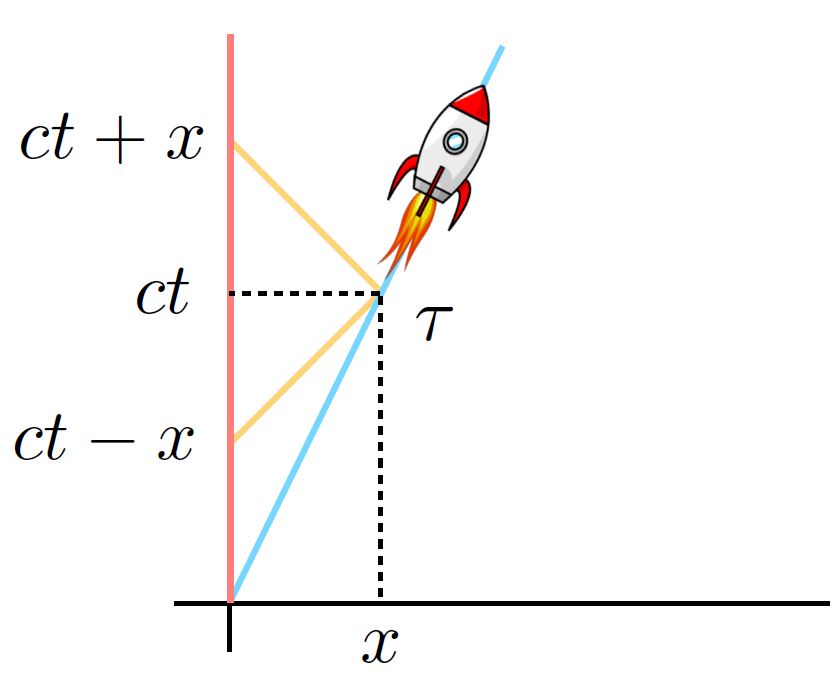
Aan de hand van het bovenstaande experiment willen we de eigentijd \( \tau \) uitdrukken in termen van de tijd \( t \) van de stilstaande waarnemer. We kunnen de informatie uit afbeelding 4 gebruiken. Omdat licht in het ruimtetijdvlak altijd onder 45 graden beweegt is het gemakkelijk om in te zien dat het eerste lichtsignaal wordt verzonden op het tijdstip \( ct – x \) gemeten op de klok van de stilstaande waarnemer. Het tweede lichtsignaal wordt ontvangen op het tijdstip \( ct + x \). We bekijken nu de verhouding tussen het tijdstip waarop de rode waarnemer het lichtsignaal uitzendt op de stilstaande klok, en dat waarop de blauwe waarnemer het lichtsignaal ontvangt op de bewegende klok. Deze verhouding wordt gegeven door:
\( \frac{ct-x}{\tau} \).
Nu komt het cruciale inzicht: we kunnen het gehele experiment ook bekijken vanuit het perspectief van de bewegende waarnemer; in dat referentiestelsel staat de ‘bewegende’ waarnemer juist stil, en beweegt de `stilstaande’ waarnemer in tegengestelde richting. Voor het tweede lichtsignaal komen we dus uit op een verhouding – tussen tijdstip van uitzenden op de nu stilstaande klok en het tijdstip van ontvangen op de nu bewegende klok – van de vorm
\( \frac{\tau}{ct+x} \).
Het relativiteitsprincipe zegt nu dat het niet uitmaakt vanuit wiens perspectief we de berekening doen1, en dat beide verhoudingen dus gelijk moeten zijn:
\( \frac{ct-x}{\tau} = \frac{\tau}{ct+x} \).
Door kruislings te vermenigvuldigen vinden we de volgende formule voor de eigentijd2:
\( \tau^2 = (ct)^2 – x^2 \).
Merk op dat deze formule lijkt op de stelling van Pythagoras die we gebruiken voor de ruimtelijke afstand tussen twee punten. Er is echter ook een groot verschil: er staat een minteken voor de tweede term aan de rechterkant. Dit is niet zonder gevolgen! Je zou kunnen zeggen dat alle verrassende verschijnselen uit de speciale relativiteitstheorie het gevolg zijn van dit minteken.
Er zijn een hoop interessante dingen die we over de formule voor de eigentijd kunnen zeggen. Bijvoorbeeld: door het minteken voor de x-coordinaat is de eigentijd \( \tau \) van de bewegende waarnemer bij een bepaalde gebeurtenis altijd kleiner dan de (herschaalde) tijd \( ct \) waarop volgens de stilstaande waarnemer die gebeurtenis plaatsvindt. Dit betekent dat volgens de stilstaande waarnemer de klok van de bewegende waarnemer trager loopt dan de stilstaande klok. Hoe sneller de andere waarnemer beweegt, hoe groter de \( x \)-coordinaat voor vaste \( t \), dus hoe kleiner de eigentijd. Dit effect heet tijdsdilatatie: bewegende klokken lopen langzamer als je ze vanuit stilstand waarneemt. De eigentijd wordt zelfs gelijk aan nul zodra de bewegende waarnemer met de lichtsnelheid gaat. Er geldt dan namelijk (vanwege het bekende ‘plaats is snelheid maal tijd’) dat \( x = ct \). Het ‘horloge van een lichtdeeltje’ lijkt voor ons dus stil te staan!
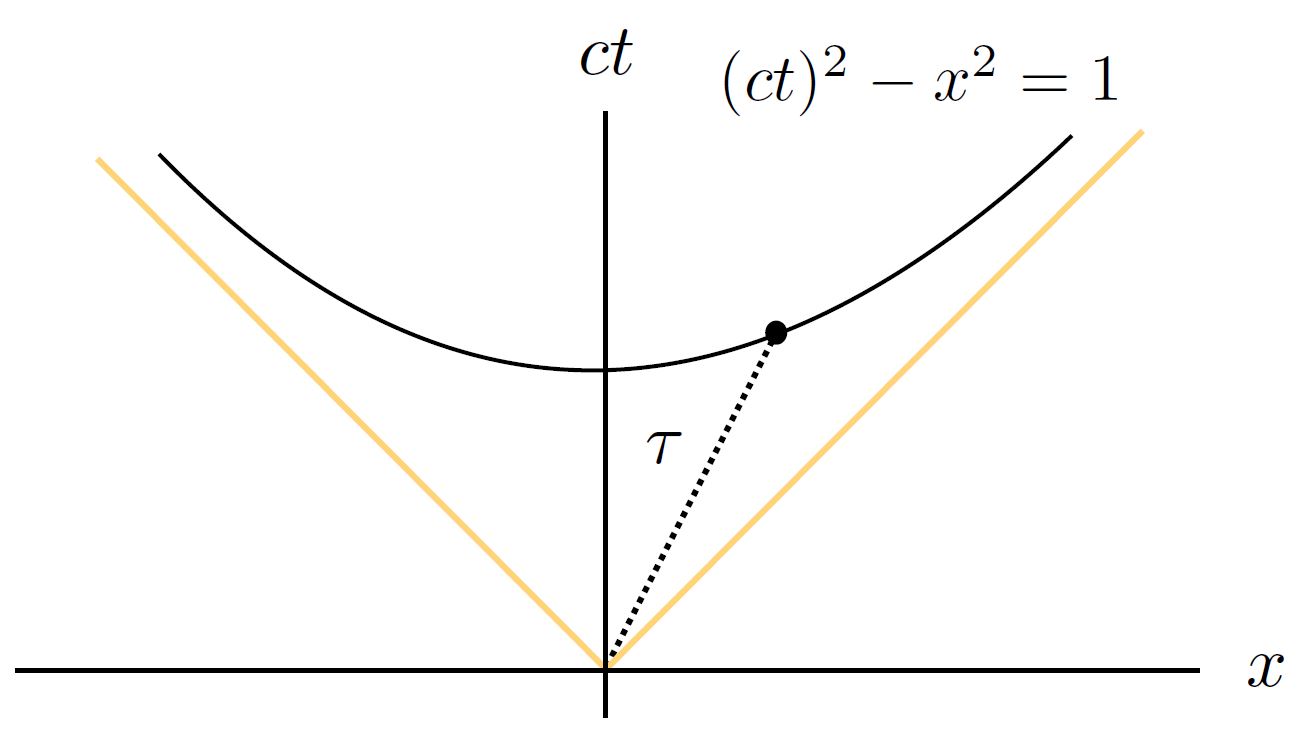
Wat zijn alle gebeurtenissen in de ruimtetijd die gelijke ‘afstand’ hebben tot de oorsprong? We kunnen dit uitrekenen door de formule voor de eigentijd iets beter te bekijken. Alle punten met eigentijd \( \tau = 1 \) – de ‘eenheidscirkel’ in de ruimtetijd – worden beschreven door de formule
\( 1 = (ct)^2 – x^2 \)
Dit is de vergelijking voor een hyperbool. Punten met dezelfde eigentijd – en daarmee met dezelfde ‘afstand’ tot de oorsprong – liggen dus niet op cirkels, maar op hyperbolen (zie afbeelding 5). Natuurkundigen denken over hun systemen graag na in termen van symmetrieën: wat kun je veranderen zodat het resultaat van een meting onveranderd – dus invariant – blijft? De transformaties die de hierboven beschreven hyperbool invariant laten zijn geen rotaties zoals bij de cirkel, maar zogenaamde boosts. Deze transformaties komen precies overeen met het veranderen van coördinatenstelsel naar dat van een bewegende waarnemer met constante snelheid. In die zin is de eigentijd een goede ‘afstandsmaat’ in relativiteitstheorie, omdat de tijd op de klok van de bewegende waarnemer ook een invariant begrip is – wat die waarnemer afleest mag natuurlijk niet afhangen van het coördinatenstelsel van degene die het geheel bekijkt.
Conclusie: we hebben gezien hoe het meten van afstanden in de ruimtetijd iets anders werkt dan we gewend zijn vanuit de ruimtelijke dimensies. Het blijkt dat de eigentijd, de tijd op een klok van een bewegende waarnemer, een goede manier is om de afstand tussen twee gebeurtenissen in de ruimtetijd uit te drukken. De formule voor die eigentijd lijkt op de stelling van Pythagoras, maar heeft een relatief minteken tussen de ruimte- en tijdsdimensie. Een enkel minteken lijkt maar een klein verschil, maar het is precies dat minteken dat zorgt voor alle bijzondere effecten uit de relativiteitstheorie!
[1] Er zit hier nog wel een addertje onder het gras: we willen vanuit beide gezichtspunten twee tijdstippen door elkaar delen: het tijdstip van uitzenden op de klok van de ene waarnemer, en het tijdstip van ontvangen op de klok van de andere waarnemer. Je krijgt dan echter alleen hetzelfde antwoord als vanuit beide gezichtspunten de klokken ook op hetzelfde moment starten. Wie van een puzzeltje houdt kan zelf proberen te controleren dat dat hier inderdaad het geval is.
[2] Als we de twee extra ruimtelijke dimensies weer introduceren wordt de formule voor de eigentijd op de vierdimensionale ruimtetijd gegeven door \( \tau^2 = (ct)^2 – x^2 – y^2 – z^2 \).