
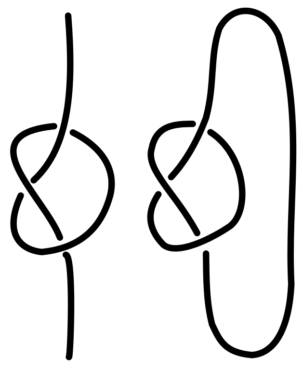
Knopentheorie beschrijft de wiskunde van knopen: het doel is om op een systematische manier de overeenkomsten en verschillen tussen knopen te bestuderen. Wat bedoelen wiskundigen precies met een knoop? Normaal gesproken denken we over knopen na in termen van een stukje touw of draad dat in elkaar is gevlochten. Zo’n knoop kun je altijd weer loshalen (al is dat in de praktijk niet altijd even makkelijk) door bij de twee uiteinden te beginnen en dan terug te werken. Omdat we geïnteresseerd zijn in de overeenkomsten en verschillen tussen knopen is het niet handig dat ze allemaal kunnen worden ontward: dan zouden ze wiskundig namelijk allemaal hetzelfde zijn. Daarom voegen wiskundigen nog een extra stap toe: nadat we de knoop hebben gelegd maken we de uiteinden van het touwtje aan elkaar vast. Wiskundige knopen zijn daarmee gesloten lusjes. In afbeelding 2 zijn de verschillen tussen ‘gewone’ knopen en ‘wiskundige’ knopen goed te zien.
Om een idee te krijgen van hoe dit werkt, is het goed om een aantal belangrijke voorbeelden te bekijken. Het simpelste voorbeeld is een samengebonden touwtje waarin helemaal geen knoop zit – een gewone cirkel dus – die heel toepasselijk de `niet-knoop’ wordt genoemd. Als je wel een knoop maakt in het touwtje voordat je de uiteinden aan elkaar maakt, krijg je niet-triviale knopen. In afbeelding 3 is een aantal voorbeelden te zien, bijvoorbeeld de klaverbladknoop en de achtknoop.
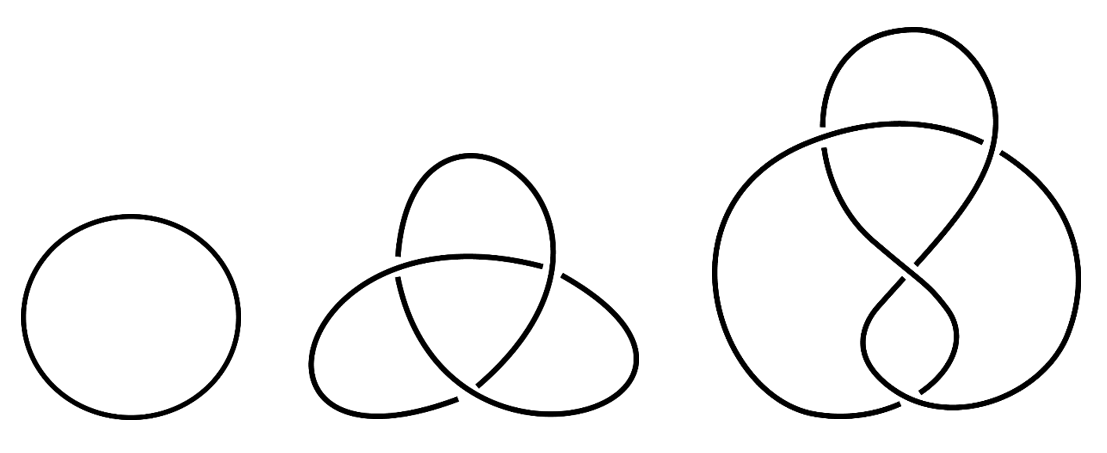
Uit de knoop?
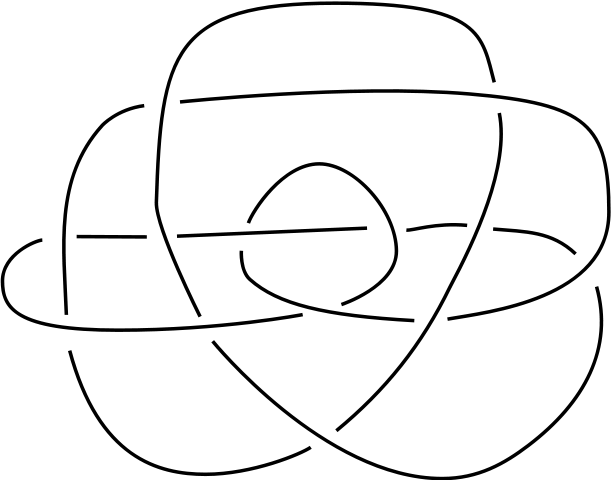
De klaverbladknoop en de achtknoop zijn niet-triviale knopen, wat betekent dat je ze niet uit de knoop kunt halen. Maar wat bedoelen we hier eigenlijk met `uit de knoop halen’? Aangezien de knopen geen uiteindes hebben, gaat het erom of je de knoop zonder te knippen of te plakken kan omvormen tot de niet-knoop. Als dit lukt heb je de knoop ontward. Na even te hebben geprobeerd kom je er al snel achter dat dit bijvoorbeeld voor klaverbladknoop niet gaat lukken. Je kunt je nu afvragen of je een knoop die er op het eerste gezicht erg ingewikkeld uitziet kunt ontwarren. Dit is over het algemeen een moeilijke vraag en vaak zit er niets anders op dan domweg proberen. Je kunt het met afbeelding 4 zelfs eens proberen (het antwoord staat in deze1 voetnoot). In afbeelding 5 is een animatie te zien van een andere knoop die ontward wordt.
Stel nu dat het je na meermaals proberen niet lukt om een ingewikkelde knoop uit elkaar te halen. Dan zou je willen concluderen dat de knoop ook echt `in de knoop’ zit. Maar het kan natuurlijk dat het ontwarren je wel was gelukt als je het nog even wat langer had geprobeerd. Hoe kun je bewijzen dat een knoop niet uit elkaar gehaald kan worden? Hier hebben wiskundigen knoopinvarianten voor uitgevonden. Het idee is dat je voor iedere knoop iets kunt uitrekenen, bijvoorbeeld een getal of een polynoom2, en dat de berekening zo in elkaar zit dat knopen die je in elkaar kunt omvormen dezelfde uitkomst hebben. De uitkomst is daarom invariant onder vervormingen. Zo heb je het bestuderen van knopen vertaald naar het bestuderen van hun invarianten, wat in het algemeen makkelijker is.
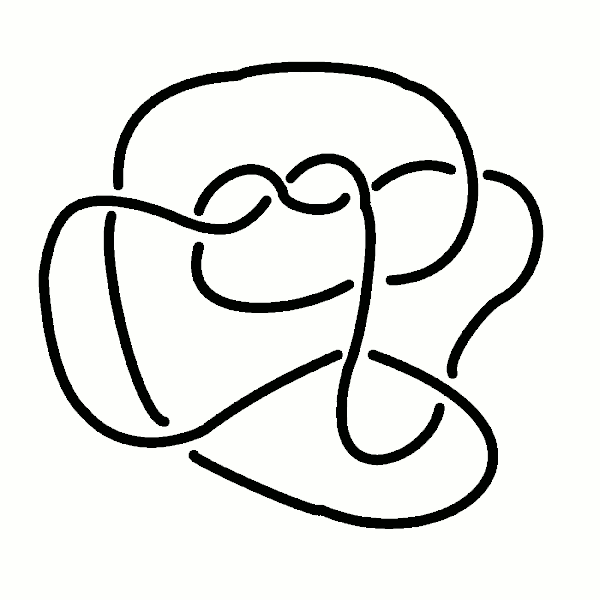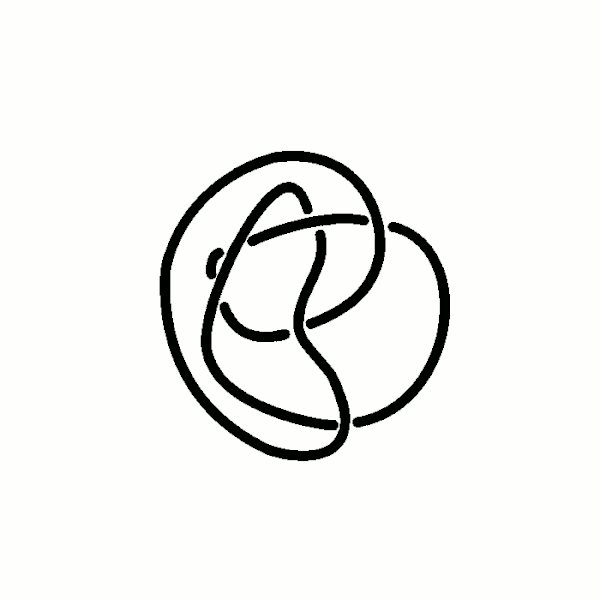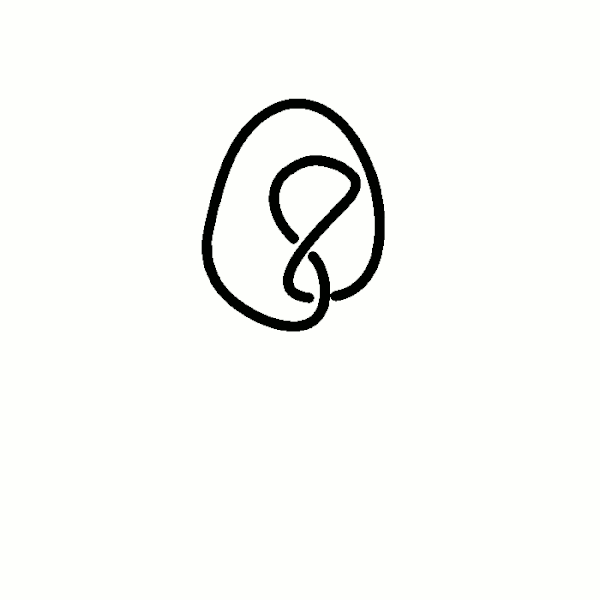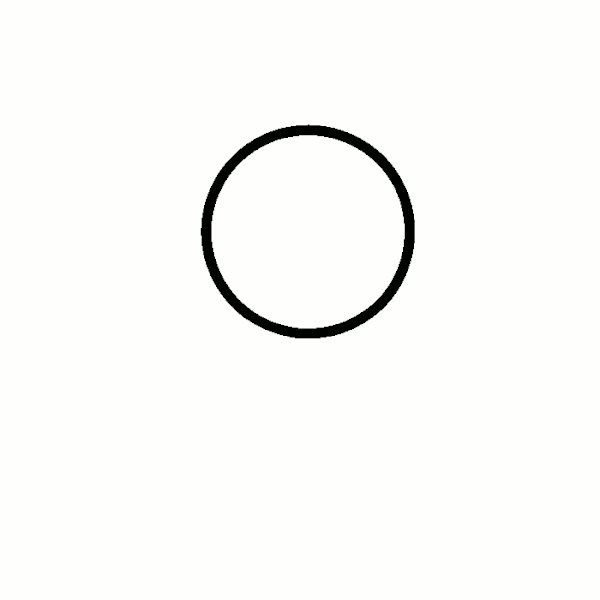
Een belangrijke knoopinvariant werd in 1984 ontdekt door Vaughan Jones. Jones bedacht een manier om voor elke knoop een polynoom J(x) te berekenen, tegenwoordig het Jonespolynoom genoemd. De precieze berekening is al eens door Mirte van der Eyden uitgelegd in een eerder artikel. Voor dit artikel is het belangrijk om te weten dat het Jonespolynoom voor de niet-knoop gelijk aan een heel eenvoudig polynoom: 1. Als je dus bij een bepaalde knoop een ingewikkelder polynoom vindt, dat niet gelijk is aan 1, dan weet je zeker dat het geen zin heeft om te proberen deze te knoop te ontwarren. Of omgekeerd: als je de knoop wel zou kunnen ontwarren, zou die het Jonespolynoom 1 moeten geven. Op deze manier kun je bewijzen dat een knoop nooit uit elkaar te halen is, hoe lang je het ook probeert.
Knoopinvarianten werken helaas maar een kant op: als je van twee knopen de invarianten berekent en de uitkomsten zijn verschillend, dan weet je zeker dat beide knopen ook verschillend zijn. Vind je echter hetzelfde antwoord, dan zijn de twee knopen niet per se in elkaar om te vormen. Ze zouden hetzelfde kunnen zijn, maar ook verschillend: de knoopinvariant geeft je dan geen nieuwe informatie. Dit probleem geldt niet alleen voor het Jonespolynoom: tot nu toe is er nog geen enkele invariant gevonden die álle knopen van elkaar kan onderscheiden. Knopentheorie houdt zich daarom voornamelijk bezig met de zoektocht naar steeds betere knoopinvarianten, die steeds meer knopen uit elkaar kunnen houden.
Knopen in de quantumfysica
Tot eind jaren 80 was de knopentheorie een volledig wiskundige onderneming. In 1989 kwam hier verandering in: de natuurkundige Edward Witten veroorzaakte toen een revolutie binnen de knopentheorie. Hij liet zien dat de natuurkunde – in het bijzonder de quantumfysica – vol zit met knoopinvarianten. De samenwerking tussen knopentheorie en quantumfysica bleek een van de meest onverwachte en succesvolle verbanden tussen wiskunde en natuurkunde. Grof gezegd is de intuïtie voor dit verband als volgt. Een centraal idee in de quantumfysica is dat je ‘alle geschiedenissen moet optellen’. Als een klassiek deeltje, bijvoorbeeld een tennisbal, van punt A naar punt B wordt afgeschoten wordt zijn baan vastgelegd door de wetten van Newton. Je kunt precies berekenen hoe dit pad eruitziet. In de quantumfysica werkt alles net even anders.
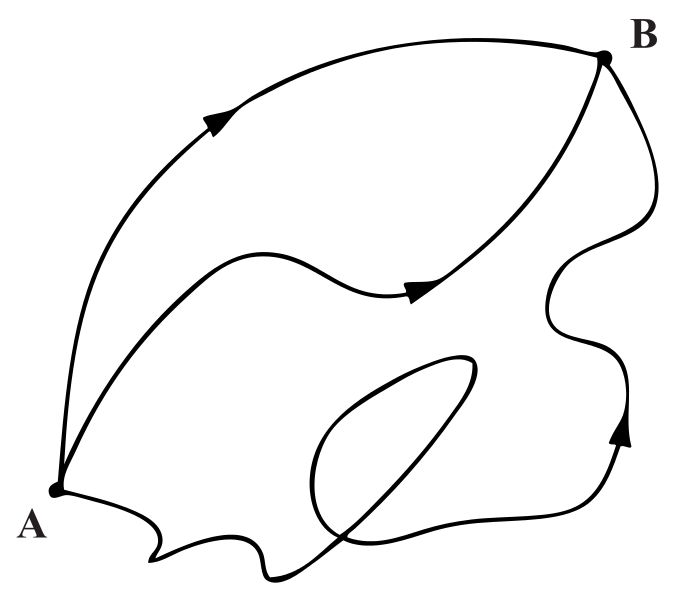
Om de baan van een quantumdeeltje van punt A naar punt B te berekenen doe je iets heel geks: in tegenstelling tot de klassieke berekening reken je in de quantumfysica alle mogelijke banen van A naar B mee, elk met een bepaalde kans. Dit is wat we bedoelen met het ‘optellen van geschiedenissen’. Hoewel het klassieke pad nog steeds de grootste kans heeft, is het in theorie mogelijk dat het deeltje een heel ander pad neemt. In bepaalde gevallen kan het pad van zo’n quantumdeeltje zelfs in de knoop zitten (zelfs in een ‘wiskundige knoop’, wanneer de punten A en B hetzelfde zijn).
Witten was geïnteresseerd in een specifieke quantumtheorie, de Chern-Simonstheorie. Chern-Simonstheorie is een voorbeeld van een ijktheorie, en lijkt daarmee erg op de theorie voor elektrische en magnetische krachten. De Chern-Simonstheorie hangt af van een keuze van ijkgroep die de symmetrieën van de theorie beschrijft. De precieze manier waarop dit werkt is niet heel belangrijk, maar het is goed om te weten dat de ijkgroep een bepaalde wiskundige structuur is waarvoor je verschillende keuzes kunt maken. Daarnaast wordt de kans op ieder quantumpad in deze theorie berekend met behulp van een zogeheten Wilsonoperator. In 1989 liet Witten zien dat de waarde van de Wilsonoperator in Chern-Simonstheorie met een specifieke keuze van de ijkgroep precies overeenkomt met het Jonespolynoom uit knopentheorie. De variabele x in het polynoom is direct gerelateerd aan de sterkte van de ‘elektrische’ kracht in Chern-Simonstheorie. Dit alles gaf een interessante interpretatie van het Jonespolynoom in de natuurkunde. En een vervolgvraag dringt zichzelf gelijk aan: wat gebeurt er als we de keuze van de ijkgroep van de Chern-Simonstheorie veranderen?
Het A-polynoom
Het bestuderen van Chern-Simonstheorie met verschillende ijkgroepen heeft tot een heleboel (nieuwe) knoopinvarianten geleid. Eén daarvan is in het bijzonder interessant om te bespreken, omdat deze invariant pas recent met de natuurkunde in verband is gebracht. Die invariant is het zogenaamde A-polynoom. In tegenstelling tot het Jonespolynoom, dat één variabele x heeft, is het A-polynoom een veelterm in twee variabelen, die vaak l en m worden genoemd. De berekening van het A-polynoom is heel anders dan die van het Jonespolynoom: het idee is dat je niet de knopen zelf, maar de complementen van de knopen met elkaar vergelijkt. Met het complement van een knoop bedoelen we het volgende: je blaast de knoop een beetje op tot een gevulde (zwem)band en vervolgens snijd je die uit de ruimte. Wat je overhoudt is precies het knoopcomplement. Er is dus een ruimte ontstaan met een knoopvormig gat, waar je niet doorheen kunt bewegen. In afbeelding 7 is bijvoorbeeld het complement van de niet-knoop weergeven, een driedimensionale ruimte waar een gevulde donut is uitgehaald.
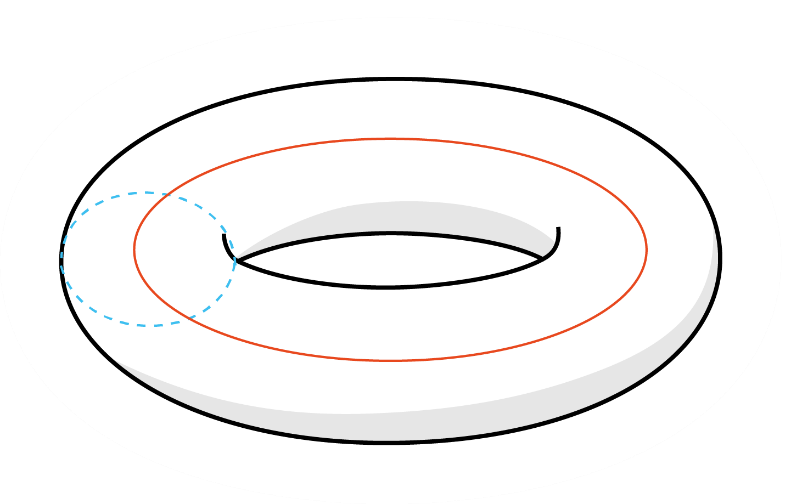
Verrassend genoeg blijken de knoopcomplementen – dus de hele ruimtes minus de knoop –gemakkelijker te classificeren dan de knopen zelf. Dit komt doordat je gebruik kunt maken van belangrijke concepten uit de topologie, de wiskunde van vormen. Zie bijvoorbeeld dit artikel voor meer toepassingen van topologie in de natuurkunde. In het algemeen heeft de rand van het knoopcomplement de vorm van een donut die in de knoop zit. Er liggen twee bijzondere lussen op deze rand, namelijk de meridiaan en longitudinaal (dat wil zeggen: de ‘breedte- en lengtegraden’). Deze lussen zijn in afbeelding 7 met rood en blauw weergeven. Er is een groot verschil tussen beide lussen: de blauwe lus gaat precies om het gat in de ruimte heen, terwijl de rode lus er als het ware op ligt. Je kunt nu proberen om de lussen als een elastiekje samen te trekken, waarbij je ze van het oppervlak af mag bewegen, maar niet de donut in (omdat daar het gat zit in het knoopcomplement). Met wat hersengymnastiek kom je er dan achter dat je de rode lus tot een punt kunt samentrekken, maar dat dit voor de blauwe niet kan.
Het A-polynoom vertelt je precies op welke manier de twee `speciale’ lussen op de donut van het knoopcomplement samentrekbaar zijn of niet. De letters l en m verwijzen hier precies naar de longitudinaal en de meridiaan. Voor de niet-knoop hebben we gezien dat de longitudinaal l samentrekbaar is in het knoopcomplement, wat in de formules wordt aangegeven met l = 1. Daarom is het A-polynoom van de niet-knoop gelijk aan
\(A(l,m)=l-1\).
wat precies nul oplevert als l = 1.
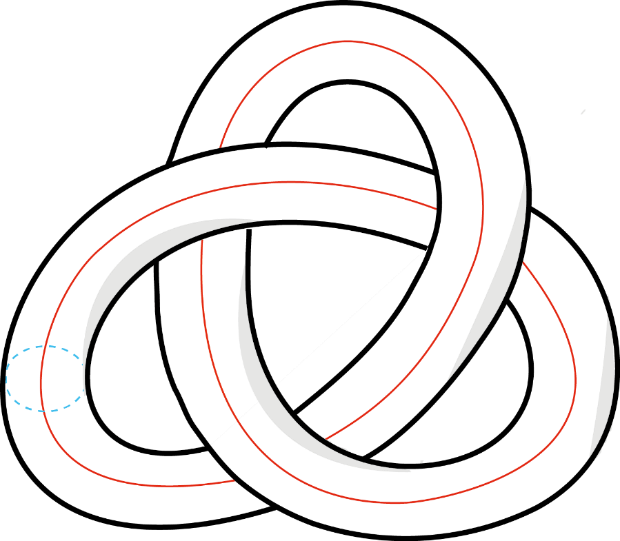
In afbeelding 8 is het knoopcomplement van de klaverbladknoop weergeven. Om het A-polynoom te berekenen moet je opnieuw kijken of de rode en blauwe lusjes samentrekbaar zijn. In tegenstelling tot de niet-knoop, zijn in dit geval zowel de blauwe als de rode lus niet samentrekbaar in het complement. Het A-polynoom blijkt daarom ingewikkelder te zijn dan bij de niet-knoop. We doen de ingewikkelde berekening hier niet, maar het resultaat ziet eruit als
\(A(l,m)=m^6 l + 1\).
Door beide A-polynomen met elkaar te vergelijken zien we direct dat de niet-knoop en de klaverbladknoop echt verschillend zijn.
De berekening van het A-polynoom en het Jonespolynoom gaan op een heel andere manier. Toch zijn wiskundigen erachter gekomen dat A-polynoom en het Jonespolynoom (gecombineerd met zijn generalisaties) heel vaak dezelfde knopen van elkaar kunnen onderscheiden. Daarom lijkt er een soort verborgen connectie tussen beide invarianten te bestaan. Opnieuw biedt de natuurkunde uitkomst! Ondanks de fundamentele verschillen in hoe je de invarianten berekent, blijkt het A-polynoom namelijk eenzelfde soort natuurkundige interpretatie te hebben als het Jonespolynoom: in termen van een Chern-Simonstheorie, maar dan met een andere ijkgroep. Vanuit de natuurkunde gezien is het dus helemaal niet zo gek dat beide polynomen veel informatie met elkaar delen.
In dit artikel hebben we gezien dat er een verborgen wereld schuil gaat achter alledaagse knopen, eentje waarin de wiskunde en de natuurkunde op een mooie manier samenkomen. De vraag of twee knopen hetzelfde zijn, blijkt veel lastiger dan je op het eerste gezicht zou denken, en om die reden hebben wiskundigen knoopinvarianten bedacht. Verrassend genoeg blijkt de quantumfysica vol te zitten met zulke knoopinvarianten: het Jonespolynoom en het A-polynoom zijn hiervan twee belangrijke voorbeelden. De innige samenwerking tussen natuur- en wiskundigen heeft op deze manier tot veel nieuwe inzichten geleid in een vakgebied dat vaak met zichzelf in de knoop zit.
[1] Dit is toch echt de niet-knoop in vermomming! Deze voorstelling van de niet-knoop is door Ochiai bedacht en is niet makkelijk om ‘in je hoofd’ los te halen. Als je hem in het echt van een touwtje maakt, wordt het een stuk makkelijker.
[2] Een polynoom of veelterm is een uitdrukking in een variabele die we vaak x noemen, bijvoorbeeld x2+3x+1.