Storingsrekening (6): Het geheel als som der delen?

Solitonen in de lucht.Dit wolkenpatroon wordt ‘stratocumulus’ of ‘Morning Glorywolk’ genoemd. Het golfvormige wolkenpatroon is een voorbeeld van een soliton. Foto: Kent Wien.

In dit artikel:

• Taylorreeksen
• Solitonen en instantonen
• Resurgence revisited

Taylorreeksen

In deze serie artikelen hebben we onszelf tot nu toe vooral de volgende vraag gesteld: als een slimme wiskundige ons een oneindige storingsreeks geeft, als oplossing van een bepaald probleem, hoe kunnen we de termen van die reeks dan optellen om het juiste natuurkundige antwoord te vinden?

We kunnen de vraag echter ook omdraaien. Stel dat het natuurkundige probleem waar we in geïnteresseerd zijn afhangt van een bepaalde parameter, x – bijvoorbeeld de grootte van een bepaalde kracht, de waarde van een elektrisch veld, of de hoogte waarop we een bal loslaten. Stel dat we bovendien de uitkomst van het probleem – de tijd die het proces duurt, de energie die erbij vrijkomt, of de temperatuur die ervoor nodig is – als functie van de parameter x, al exact kennen. Laten we die uitkomst schrijven als f(x). Kunnen we dan ook een storingsreeks vinden, natuurlijk ook afhankelijk van x, die die uitkomst beschrijft?

Afbeelding 2. Brook Taylor.De Engelse wiskundige Brook Taylor (1685-1731).

Het antwoord op deze vraag is al sinds de vroege 18e eeuw bekend, en werd voor het eerst formeel uitgeschreven door Engelse wiskundige Brook Taylor. Het idee van Taylor begint met de volgende eenvoudige observatie: als de waarde van x heel klein is, wordt f(x) vaak heel goed benaderd door f(0). Het verschil tussen f(x) en f(0) wordt groter naarmate x groter wordt, en in eerste instantie is die toename proportioneel met x zelf. De proportionaliteitsconstante heet de afgeleide van f(x) in het punt x=0; een hele mond vol, die meestal wordt afgekort tot f'(0). Een betere benadering van f(x) is daarmee dus

f(x) ≈ f(0) + x f'(0)

Deze redenering kan herhaald worden: het verschil tussen de exacte waarde van f(x) en de benadering die hierboven rechts van het ≈-teken staat, blijkt proportioneel te zijn met het kwadraat van x. De proportionaliteitsconstante (op een conventionele factor 1/2 na) heet de tweede afgeleide, en wordt ook wel geschreven als f”(0). Ook die benadering is weer niet perfect: de volgende correctieterm is proportioneel met de derde macht van x, enzovoort. De volledige uitdrukking die Taylor opschreef was daarmee:

f(x) ≈ f(0) + x f'(0) + x² f”(0) / 2 + x³ f”'(0) / 6 + …

De getallen onder de deelstrepen zijn weer de faculteiten die we ook in het vorige artikel tekenkwamen: 1, 1 × 2, 1 × 2 × 3, enzovoort.

Naar boven

Solitonen en instantonen

De oplettende lezer is het misschien opgevallen dat in de laatste uitdrukking hierboven nog altijd een ‘ongeveer gelijk’-teken (≈) staat. Betekent dat dat zelfs de oneindige Taylorreeks aan de rechterkant de functiewaarde f(x) niet altijd perfect benadert? Dat blijkt soms inderdaad het geval te zijn! Een voorbeeld van een functie die dit probleem vertoont zijn we in afbeelding 3 hieronder.

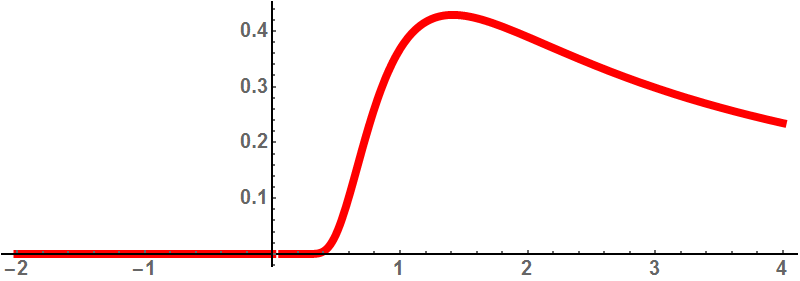
Afbeelding 3. Een soliton.Van de hierboven getekende functie zijn alle afgeleides in het punt x=0 gelijk aan 0. Toch is de functie zelf voor geen enkele x > 0 gelijk aan 0!

Op de horizontale as staat de waarde van x uitgezet; op de verticale as de waarde van f(x). (Voor de wiskundeliefhebbers: de functie die we hier gekozen hebben voor x > 0 is f(x) = exp(-1/x²) / x.) Voor waarden van x kleiner dan 0 is de functie exact gelijk aan 0. Vanaf x=0 begint de functie te groeien, al is dat in eerste instantie nog niet heel goed te zien. Pas vanaf ongeveer x=0,2 neemt de functie zichtbaar toe, maar ook voor kleinere waarden van x is f(x) een fractiegroter dan 0. De functie stijgt daar echter zó langzaam dan niet alleen de functiewaarde in x = 0 gelijk is aan 0, maar ook de afgeleide, de tweede afgeleide, enzovoort! Met andere woorden: de Taylor-reeks voor de functie is

0 + 0 x + 0 x² + 0 x³ + …

en is dus exact gelijk aan 0! Voor waarden van x die groter zijn dan nul, geeft de Taylor-benadering dus duidelijk niet het juiste antwoord. Het geheel lijkt in zekere zin méér te zijn dan de som der delen…

Een functie zoals die hierboven, die door de Taylor-reeks ‘niet gezien’ wordt, wordt een soliton genoemd. Zulke solitonen komen in de natuurkunde veelvuldig voor. Soms gaat het daarbij om abstracte functies f van ingewikkelde variabelen x, maar soms kan de hierboven getekende ‘golf’ ook heel letterlijk genomen worden. Zo bestudeerden de Nederlandse wiskundigen Diederik Korteweg en Gustav de Vries aan het einde van de 19e eeuw een wiskundig model dat watergolven in een ondiep water beschrijft. De vergelijking waarmee ze die golven beschreven, staat tegenwoordig dan ook bekend als de Korteweg-de Vriesvergelijking. Een studie van deze vergelijking toonde aan dat watergolven in ondiep water exact het hierboven beschreven gedrag vertonen: er zijn soliton-vormige golven die vanaf een afstand vrijwel onmeetbaar zijn, net zoals vanaf een punt x<0 in de grafiek hierboven de ‘golf’ rechts niet zichtbaar is in de afgeleiden van de functie.

Afbeelding 4. Solitonen in ondiep water.Foto: Michel Griffon.

Overigens kan de parameter x ook bijvoorbeeld de tijd zijn. In dat geval moeten we een verschijnsel als hierboven letterlijk zien als iets wat we niet kunnen zien aankomen: op tijdstippen voor x=0 is de functie onveranderlijk, waarna er plotseling – instantaan – een bepaalde fluctuatie optreedt. In dit geval wordt een dergelijk verschijnsel ook wel een instanton genoemd.

Naar boven

Resurgence revisited

We lijken daarmee op een tweede grote probleem rond storingsreeksen te zijn gestuit: bepaalde verschijnselen lijken met behulp van zulke storingsreeksen niet ‘zichtbaar’ te zijn, omdat de Taylorreeks geen informatie erover bevat.

Verrassend genoeg blijkt ook hier het idee van resurgence dat we in het vorige artikel tegenkwamen, een oplossing te bieden. We zagen daar dat sommige storingsreeksen een heel ander probleem hebben: ze benaderen de gewenste uitkomst in eerste instantie goed, maar als nog meer termen meegerekend worden uiteindelijk weer slechter. We zagen ook hoe dit probleem uiteindelijk, met behulp van technieken ontdekt door de Franse wiskundige Émile Borel, opgelost kon worden, en hoe zo’n storingsreeks omgezet kan worden in een voorschrift om tóch de juiste uitkomst te vinden.

Wat Borel nog niet wist, maar wat bijna een eeuw later door de Franse wiskundige Jean Écalle ontdekt zou worden, is dat met exact diezelfde technieken nog veel meer informatie over functies f(x) beschikbaar komt. Na Borelsommatie blijkt namelijk niet alleen dat de storingsreeks tot een goedgedefinieerd antwoord leidt: dat antwoord bevat óók eventueel aanwezige solitonen en instantonen. Sterker nog: als in een proces een soliton blijkt voor te komen, kunnen we zo’n soliton zélf beter onderzoeken door ook in de buurt daarvan weer een storingsreeks op te stellen, en ook de informatie over díe storingsreeks blijkt na Borelsommatie bevat te zijn in de oorspronkelijke storingsreeks. Dit is de eigenlijke achtergrond van de naam resurgence, of ‘herrijzenis’: de informatie over solitonen, en de storingsrekening rónd die solitonen, blijkt uiteindelijk exact gecodeerd te zijn in de oorspronkelijke storingsreeks. Kortom: het geheel is nog altijd de som der delen, alleen moeten die delen wel eerst op de juiste manier bestudeerd worden.

Daarmee blijkt storingsrekening nog een veel krachtiger middel dan altijd gedacht werd. Het onderzoek naar ‘resurgente eigenschappen’ van allerlei storingsreeksen die in de natuurkunde voorkomen staat de laatste tijd sterk in de belangstelling. Juist omdat we in de natuurkunde problemen vaak niet exact op kunnen lossen, is de storingsrekening een veelgebruikt gereedschap – en het lijkt erop dat dit gereedschap nog veelzijdiger is dan we dachten!

Naar boven

Het volgende artikel in deze reeks verschijnt op vrijdag 29 januari. In dit voorlopig laatste artikel over dit onderwerp zullen we een heel belangrijke natuurkundige toepassing van al het voorgaande bespreken: storingsreeksen in de quantumveldentheorie.