
Getaltheorie is dus de studie van eigenschappen van gehele getallen: 1, 2, 3, enzovoort – en eventueel ook 0 en de negatieve gehele getallen. De eigenschap die we in dit artikel bestuderen is als volgt. Voor een geheel getal n, laten we zeggen groter dan 0, is de vraag op hoeveel manieren we dat getal als som van andere positieve gehele getallen kunnen schrijven. Met andere woorden: hoeveel partities heeft een positief geheel getal? Voor kleine getallen is dat vrij simpel:
1: 1
2: 2, 1+1
3: 3, 2+1, 1+1+1
4: 4, 3+1, 2+2, 2+1+1, 1+1+1+1
We kunnen een functie p(n) definiëren die voor een getal n het aantal partities van n als functiewaarde heeft. De eerste paar waarden van deze functie zijn zoals je hierboven kunt natellen, dus p(1)=1, p(2)=2, p(3)=3 en p(4)=5. Je kan al snel zien dat p(n) snel groeit als n toeneemt. Maar kunnen we kwantificeren hoe snel?
Een manier om zo’n vraag te beantwoorden is door te kijken naar de genererende functie van p(n). Dat betekent dat we op zoek gaan naar een functie f(x) zodat
\( f(x) = \sum_{n=0}^\infty p(n) x^n = p(0) + p(1) x + p(2) x^2 + p(3) x^3 + \ldots \)
Om de functie f te vinden gebruiken we een Taylorreeks, een wiskundig hulpmiddel dat al eerder besproken werd in dit artikel. Als x kleiner is dan 1 hebben we de volgende gelijkheid:
\( \frac{1}{1-x} = \sum_{n=0}^\infty x^n = 1 + x + x^2 + \ldots \)
Probeer dat bijvoorbeeld zelf te controleren door x = ½ in te vullen en in te zien dat je zowel links als rechts van het gelijkteken het antwoord 2 krijgt. Door in bovenstaande vergelijking x te vervangen door een macht van x vinden we ook:
\( \frac{1}{1-x^j} = \sum_{n=0}^\infty x^{nj} = 1 + x^j + x^{2j} + \ldots \)
We kunnen nu deze gelijkheden gebruiken om de genererende functie voor p bepalen. Bekijk de functie g(x) die is gegeven door
\( g(x) = \prod_{j=1}^\infty \frac{1}{1-x^j} = \frac{1}{(1-x)(1-x^2)(1-x^3)(1-x^4)\cdots} \)
Door gebruik te maken van de Taylorreeksen voor elk van de factoren in bovenstaand product kunnen we zien dat deze functie g precies de genererende functie voor p(n) is! De functie die we hierboven g noemen, is dus precies de functie f die we zochten. Voor kleine getallen kunnen we expliciet zien dat die bewering waar is. Voor machten van x tot en met 4, hebben we bijvoorbeeld alleen de eerste vier factoren van g nodig, aangezien de Taylorreeksen behorende bij die factoren als enige machten van x kleiner of gelijk aan 4 bevatten. We zien dan door alle haakjes uit te werken dat
\( \begin{eqnarray} && \frac{1}{(1-x)(1-x^2)(1-x^3)(1-x^4)\cdots} \\ && \quad = (1+x+x^2+x^3+x^4+\ldots) (1+x^2+x^4+\ldots) (1+x^3+\ldots) (1+x^4+\ldots) \cdots \\ && \quad = 1 + x + 2 x^2 + 3 x^3 + 5 x^4 + \ldots \end{eqnarray} \)
Reken het vooral zelf na! De Taylorreeksen genereren zo precies de partities van de gehele getallen die we eerder hebben bepaald. De intuïtie achter dit verrassende resultaat is als volgt: de eerste factor \( \frac{1}{1-x} \) telt het aantal enen in de partitie, \( \frac{1}{1-x^2} \) telt het aantal tweeën, en \( \frac{1}{1-x^j} \) telt het aantal j’s in de partitie. Laten we als voorbeeld p(4) bepalen op deze manier. We zoeken daarvoor de coëfficiënt in de totale uitdrukking van g die vermenigvuldigt. De verschillende manieren om te krijgen zijn
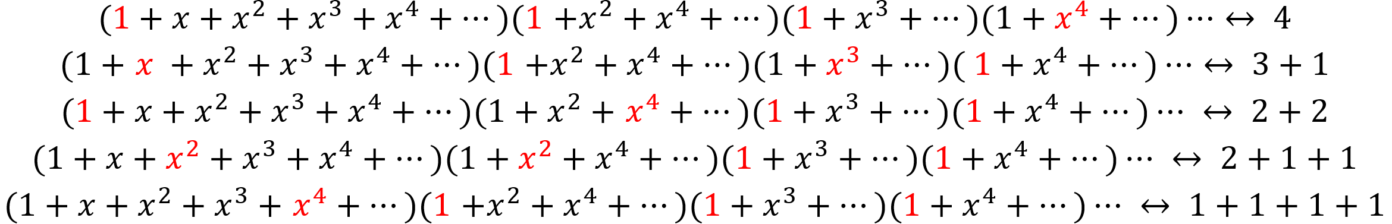
Merk op dat de factoren 1 in de vermenigvuldiging helemaal niets tellen – 1 kun je namelijk schrijven als x0. De overige factoren in elke manier corresponderen precies met de verschillende partities van 4.
We hebben nu dus de genererende functie f gevonden, en om het aantal partities van een getal n te vinden hoeven we alleen de coëfficiënt die \( x^n \) vermenigvuldigt in f te bepalen. Voor lage waarden van n is dit simpel en kan het met de hand, zoals we hierboven deden. Voor grotere waardes kunnen computers helpen, maar voor de limiet \( n \to \infty \) bieden zelfs computers geen soelaas. Om deze limiet te begrijpen kan de kracht van getaltheorie ons helpen.
Eerst definiëren we nóg een functie die gerelateerd is aan de partities. Dit is de Dedekind-eta-functie:
\( \eta(\tau) = q^\frac{1}{24} \prod_{n=1}^\infty (1-q^n), \qquad \mbox{waar} \; \; q = e^{2\pi i \tau} \).
De Dedekind-eta-functie is vernoemd naar de Duitse wiskundige Richard Dedekind. Het is een zogenaamde modulaire vorm met gewicht ½. Dat is een mondvol, maar het betekent dat de functie simpele eigenschappen heeft onder bepaalde transformaties:
\( \eta(\tau+1) = e^\frac{\pi i}{12} \eta(\tau) \qquad \mbox{en} \qquad \eta(-1/\tau) = \sqrt{-i \tau} \; \eta(\tau) \).
Bewijzen dat deze eigenschappen gelden – zeker de tweede – is overigens nog niet zo eenvoudig! Wat voor dit verhaal van belang is: de Dedekind-eta-functie blijkt gerelateerd te zijn aan de genererende functie voor de partities, f, volgens
\( f(q) = \frac{q^{1/24}}{\eta(\tau)} \).
Nu denk je misschien: mooi, nog een functie, deze keer met handige eigenschappen, maar wat zijn we hier nou mee opgeschoten? Een heleboel! We kunnen deze eigenschappen namelijk gebruiken om het gedrag van p(n) in de limiet \( n \to \infty \) te bepalen. Dit gedrag is op een simpele manier gerelateerd aan het gewicht van de modulaire vorm \( \eta \). Op de precieze wiskunde daarachter komen we misschien in een vervolgartikel nog eens terug, maar als je gebruikt dat de eta-functie gewicht ½ heeft en de technieken uit de getaltheorie omtrent dit soort modulaire vormen volgt, vind je dat
\( p(n) \sim \frac{1}{n} e^{\sqrt{n}}, \qquad \mbox{als} \; \; n \to \infty \).
Dit is een interessant antwoord op een vraag die erg simpel lijkt, maar waarvoor zoals je ziet ingewikkelde technieken nodig zijn om hem te beantwoorden. Er schuilen echter meer geheimen achter dit soort simpele vragen – en daarbij komt naast de wiskunde ook de natuurkunde om de hoek kijken. Op deze site schreven we bijvoorbeeld eerder over het aantal mogelijke toestanden van zwarte gaten, en hoe we die kunnen tellen: zie bijvoorbeeld dit artikel en het vervolgartikel daarop. Daar wordt beschreven hoe het aantal mogelijke toestanden van een zwart gat geteld kan worden aan de hand van het oppervlak van het zwarte gat. Het is echter onduidelijk wat precies de microscopische toestanden zijn die worden geteld door het oppervlak – welke bouwstenen er dus überhaupt geteld worden. Wat blijkt nu: in de snaartheorie kun je wel bedenken wat die bouwstenen zijn – het zijn de zogeheten D-branen – en wordt het aantal microscopische toestanden vaak beschreven door een modulaire vorm, zoals bijvoorbeeld \( \eta \). Als we p(n) ‘vertalen’ naar natuurkundetaal, vinden we zo in de asymptotische expansie van p precies de formule voor de entropie van een zwart gat. Zo kun je bijvoorbeeld ontdekken dat de wortel van n die je in bovenstaande formule ziet staan, vertaald kan worden naar de oppervlakte van een zwart gat!
De voorbeelden uit dit artikel – hoewel die al flink ingewikkeld zijn – zijn nog maar het topje van de ijsberg. Resultaten uit de getaltheorie geven in de moderne natuurkunde allerlei inzichten in de microscopische toestanden die tot de thermodynamische eigenschappen van zwarte gaten leiden.