
Die vraag is zonder twijfel te ingewikkeld om een eenvoudig antwoord te hebben. Het is desondanks opmerkelijk dat kriticiteit, een begrip waar natuurkundigen uitgebreid kennis mee hebben gemaakt, telkens weer verschijnt in verschillende biologische systemen. Waarom dit überhaupt zou gebeuren, blijft vooralsnog vaak geheimzinnig, maar wordt langzaam verduidelijkt door zowel natuurkundigen als biologen.
Kriticiteit1 is het idee dat een theorie onder bijzondere omstandigheden bestudeerd wordt — waarbij de parameters heel specifieke waarden nemen. Vaak betekent dit dat het beschreven systeem tussen twee verschillende regimes in zit — denk voor een eenvoudig voorbeeld aan water tussen zijn vloeibare vorm en zijn vaste vorm. In een iets diepere zin betekent zo’n kritiek punt dat de theorie van orde naar wanorde gaat — bijvoorbeeld in het voorbeeld van de spins van het Isingmodel, waar kriticiteit precies gebeurt tussen het regime waar de spins in grote gebieden — van een bepaalde schaal — in dezelfde richting wijzen, en het regime waar de spins fluctueren over een karakteristieke eindige lengte. Precies óp het kritieke punt komen juist correlaties voor op alle verschillende afstandsschalen. Zo vernietigt kriticiteit het idee van de karakteristieke lengte in de theorie die anders wel altijd bestaat. Je zou ook kunnen zeggen dat die karakteristieke lengte naar oneindig gaat.2
Ik besprak hierboven voorbeelden waar je op de kriticiteit terecht kunt komen door het veranderen van een parameter — bijvoorbeeld, in het Isingmodel, de sterkte van het magnetische veld. Wat in de biologie opvalt, is dat systemen zelf vaak zulke kritieke punten lijken te bereiken. We noemen dit zelfgeorganiseerde kriticiteit.
In het klimaat verschijnt zelfgeorganiseerde kriticiteit overal. Verdelingen van bosbranden volgen bijvoorbeeld de regel dat, hoe groter het vuur is, hoe minder vaak zo’n bosbrand voorkomt. Preciezer: de frequentie neemt af met de grootte volgens een machtswet.3 Dit laatste betekent dat er geen enkele karakteristieke lengte is — je kunt wiskundig laten zien dat je dan een ander verband anders zou verwachten, namelijk een exponentiële relatie. Inderdaad is zo’n machtswetrelatie het belangrijkste teken van kriticiteit, en natuurkundigen maken er dus graag gebruik van om de gegevens te ontleden. Soortgelijke verhoudingen kan je bijvoorbeeld ook terugvinden in de verdelingen van lawines en aardverschuivingen. In de biologische wereld verschijnen ze in de verdelingen van de neurale activiteit in de hersenen.
Wat hier ook belangrijk is, is de macht zelf — het getal dat in de machtswetrelatie verschijnt. Aangezien dat getal met geen enkele lengteschaal geassocieerd is, is het in die zin universeel en heeft het niets te maken met bijzondere omstandigheden of systemen. De macht die voorkomt in de relatie voor bosbranden is gewoon een kenmerk van die branden zelf en zegt iets dieps over het verschijnsel. In de natuurkunde noemen we deze getallen kritische exponenten.
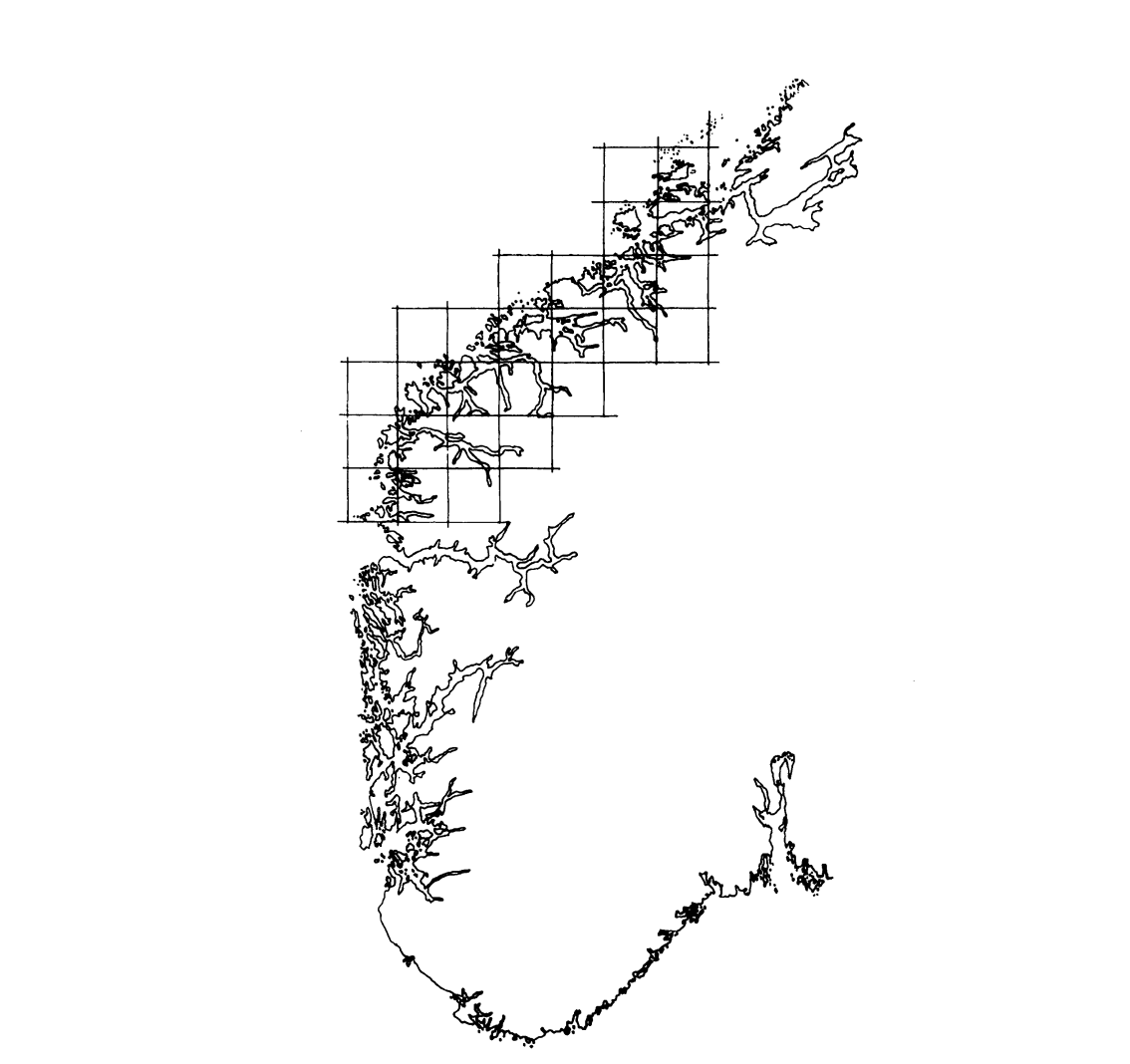
Schaalinvariantie heeft niet alleen met de frequentie van gebeurtenissen te maken, maar bijvoorbeeld ook met het uiterlijk van objecten in de natuur. Als je op de vorm van de kust van een land als Noorwegen inzoomt, krijg je schijnbaar hetzelfde beeld — niet letterlijk, natuurlijk, maar de structuur verandert niet of nauwelijks. Van dit verschijnsel uit de wiskunde heb je misschien wel eens gehoord: zo’n structuur heet een fractal. Ze vormen ook in de natuur belangrijke voorbeelden van kritische punten. Zulke fractalen zie je ook in rivierbeddingen, waarvan de vormen vaak bepaald worden door twee gerelateerde processen: de vloeistofstroom en de sedimentatie. Als de fractal niet in de ruimte zelf hoeft voor te komen, maar in plaats daarvan in bijvoorbeeld een grafiek van de frequentie van ruis, kan je nog meer voorbeelden van kriticiteit ontdekken — in dit voorbeeld verzameld onder de naam 1/f noise. We zien in de natuur heel vaak dat de zogeheten spectrale dichtheid van de ruis omgekeerd evenredig is met de frequentie, maar in de meeste gevallen hebben we daar nog steeds geen verklaring voor!
Het is dus opvallend hoeveel systemen in de natuur kriticiteit vertonen — maar er bestaat nog discussie over hóé zulke systemen zelfgeorganiseerd worden. Enerzijds is duidelijk dat de biologische wereld meestal geen ‘beheerder’ heeft die parameters kan selecteren en zo kriticiteit kan bereiken. Wat er gebeurt, is dus het gevolg van natuurlijke processen, en niets meer.
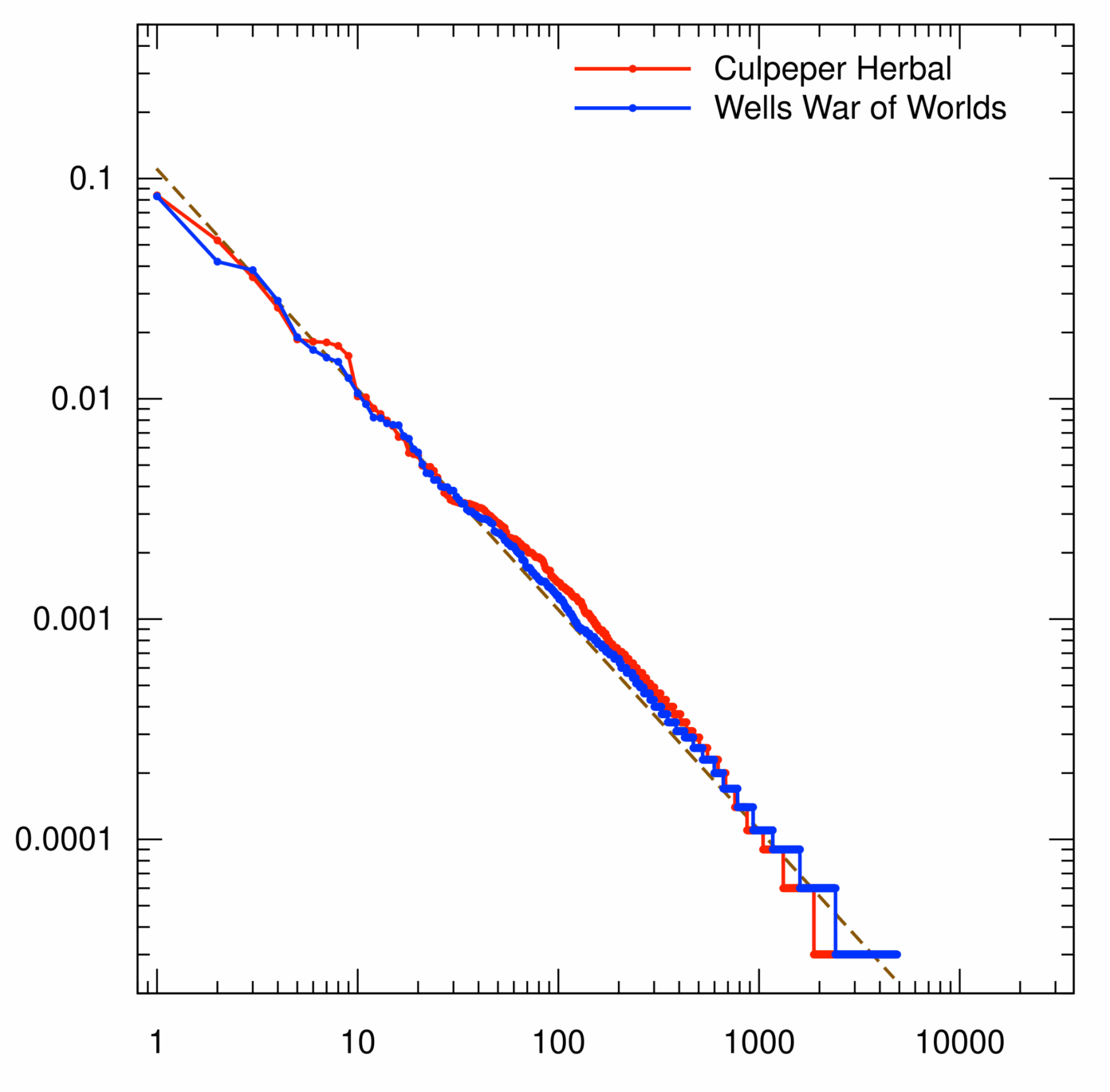
Is zelforganisatie echter anderzijds ook alleen maar een gevolg van kansprocessen? Hier blijkt het antwoord af te hangen van het specifieke geval. De frequentie waarmee woorden in een taal worden gebruikt is een alledaags voorbeeld: die blijkt geheimzinnig af te nemen in omgekeerd evenredige verhouding met de positie op een meestgebruikte-woordenlijst. Dit wordt de wet van Zipf genoemd, en wordt in diverse andere contexten ook waargenomen. Als dat je niet verrast, besef dan dat er geen enkele reden bestaat waarom zo’n verband in het algemeen zo zou bestaan! Het tweede woord op de lijst hoeft niet (bijna altijd) precies twee keer minder voor te komen dan het eerste — het had ook vier keer minder kunnen zijn, bijvoorbeeld — noch het derde drie keer minder, enzovoort. Hier zien we weer het idee van 1/f-ruis. Sommige wetenschappers, zoals Zipf zelf, hebben voorgesteld dat de wet volkomen verklaarbaar is op basis van gewone willekeurigheid, plus een aantal aannames over de verdeling van woorden, maar andere wetenschappers zijn het daar in verschillende gevallen niet mee eens.
Natuurkundigen zijn vooral geïnteresseerd in een mechanisme dat de veelvoorkomende zelforganisatie kan verklaren, en ontwikkelen nu theorieën die dat kunnen. Een mogelijke benadering is om een eenvoudiger model op te stellen dat zijn eigen overgang naar kriticiteit duidelijk laat zien, zonder het besturen van parameters. Zoiets werd al met het zandstapelmodel gedaan, waar zanddeeltjes volgens bepaalde wetten bewegen en stapels kunnen instorten. In dit model konden natuurkundigen zien dat kriticiteit ontstond, en bovendien het mechanisme waardóór het ontstond. Ze noemden dat een cascade, een situatie waarbij een kleine gebeurtenis een grote kettingreactie veroorzaakt waarbij energie zich op alle lengteschalen verplaatst. Soortgelijke ideeën werden vervolgens beter begrepen en ook op onze eerdere voorbeelden van lawines en bosbranden toegepast, waarvoor ze ook natuurlijk geschikt bleken.

We leren elke dag meer over het onderwerp van zelfgeorganiseerde kriticiteit, maar er blijven nog vele raadselen in dit onderwerp, dat uitzonderlijk verschillende vakgebieden samenbrengt en gaat over de geheimen van zowel alledaagse als exotische verschijnselen.
[1] Er is geen heel gangbare term voor het verschijnsel in het Nederlands; in het Engels wordt meestal criticality gebruikt.
[2] Hieraan kan je ook zien dat kriticiteit met symmetrieën te maken heeft — in het voorbeeld met de spins is het kritieke punt het punt waarop de zogenoemde Z₂-symmetrie (die zegt dat ‘up’ en ‘down’ even vaak voorkomen) ontstaat of juist gebroken wordt.
[3] Een machtwet betekent dat het ene verschijnsel bijvoorbeeld schaalt als het kwadraat, de derde macht, of een andere macht van het andere verschijnsel.