
Evolution has also done something else to humans; it has programmed us to be very good at recognizing patterns. The epitome of recognizing patterns is our preference for and affinity towards ‘symmetry’. Symmetry can be audio-visual, like in music or painting, as well as more abstract and mathematical. It is the more abstract and mathematical form of symmetry that physicists and mathematicians are trained to identify and analyse. In fact, the quest for symmetry has driven most of modern physics in the past century. When applied to the context of gravitational systems, the concept of symmetry comes alive in a specific incarnation which we call ‘asymptotic symmetries’. The rest of this article is a conceptual overview of what ‘symmetry’ means in physics, and specifically what ‘asymptotic symmetries’ are. Since no physicist wastes their time on things that they believe aren’t useful in understanding some aspect of the world, this article will also describe the importance of asymptotic symmetries in understanding the universe at a deeper level.
What is ‘symmetry’? How would you define it and describe it precisely? The reader might complain at this point, saying to themselves “Symmetry is symmetry! You know it when you see it. You see a symmetric object and you just know. There’s no use in being pedantic about what symmetry is more abstractly.” But, as you know, in physics and mathematics, if you wish to make unambiguous statements about the world, you have to be very precise about the concepts you use. Thus, here is what physicists mean by symmetry: an object has a symmetry if you do something specific to it and some aspect of the object does not change.
Now, for a reader for whom this is the first exposure to symmetries, the above statement might look absolutely redundant. It turns out, however, that it is a powerful definition of the idea of symmetry and proves to be very useful in physics. Let’s start with a simple example. Consider an ice crystal, as shown in the image. Now, in the spirit of the definition above, we decide to do something specific to the crystal, namely rotate it around its centre, by \( 60^{\circ} \). After being rotated (and the crystal is really being rotated, as you can tell from the rotation of the rectangular shape of the photo), you will notice that the crystal still looks the same. Its appearance is constant despite rotations. In the spirit of the above definition, this crystal therefore has a rotational symmetry.
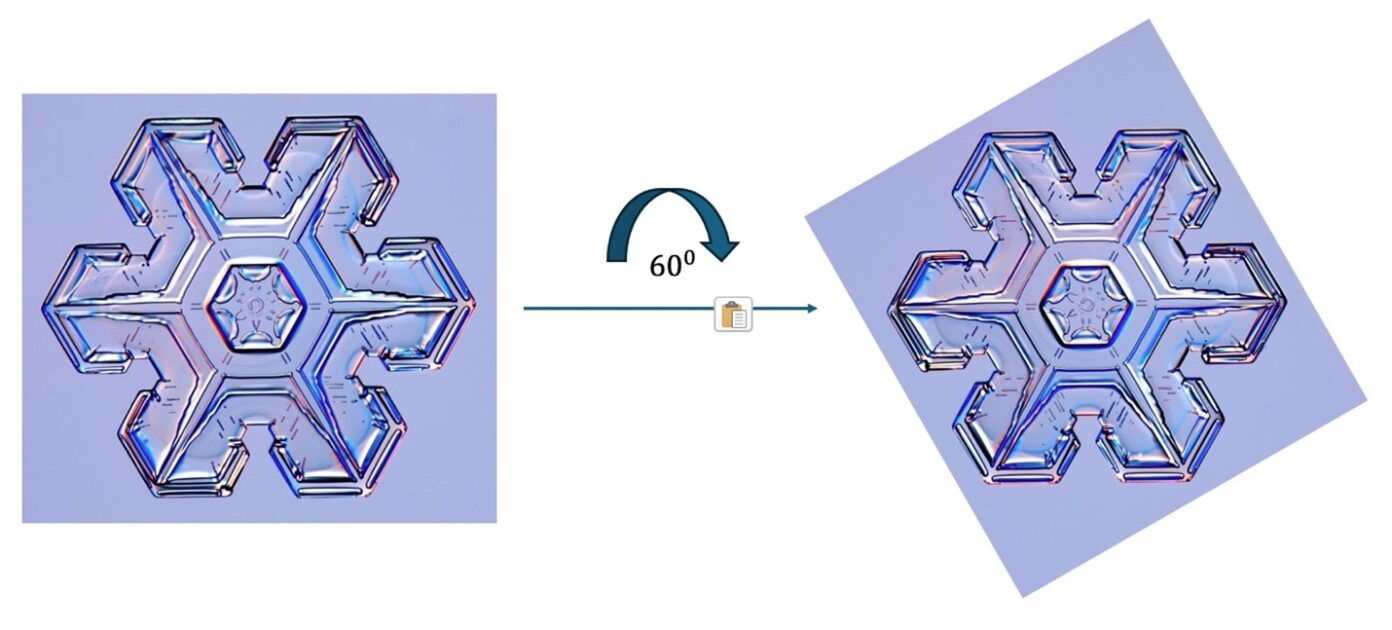
Now comes a creative step which makes the whole field of symmetries more mathematical and slightly more abstract than visual rotations of images. There is an equivalent way to describe the rotational symmetry of a crystal. Since the crystal is a 2D object, you impose an X-Y grid on the crystal, with the origin of the X-Y coordinate system coinciding with the center of the crystal. Then, all statements about the rotational properties of the crystal have a rhyme in the rotational properties of the X-Y plane imposed upon it. Specifically, you can rotate the axes of the grid by \( 60^{0} \) in either direction about the origin. With respect to these new axes, the crystal will look exactly the same as it looked with respect to the unrotated axes.
Therefore, in the spirit of our definition of symmetry, the rotational symmetry of the crystal emerged as an answer to the following question: ‘In which ways can I change the coordinate system imposed upon the crystal such that the crystal looks the same?’ One answer is: ‘you can rotate it about its center by \( 60^{0} \).’ Collect all possible answers to the question, and you know exactly what the symmetry of a crystal is!
The ideas of symmetry do not just apply to objects inside the universe. These ideas can also be applied to the universe itself. Next question: what symmetry properties does the universe have? What does that even mean? Let’s take a look. You have no doubt read that Albert Einstein famously modelled the universe which we live in as a four-dimensional geometric object called ‘spacetime’. Before we embark on the description of the symmetries of a universe with gravity in it, let us first tackle a slightly easier problem. What about the symmetry properties of a world with no gravity in it? This is a world governed by Einstein’s theory of special relativity. In this scenario, the world which we live in is modelled as nothing but the usual three-dimensional space that we know from Newton, plus an extra direction of time. Imagine such a universe to be completely empty, i.e. no galaxies, no comets, no asteroids, no black holes, etc.
Now, let us impose a coordinate system on such a spacetime: \( \left(t,x,y,z\right) \). The principles of special relativity imply that given any two points (or really: events, since these ‘points’ also have a time coordinate) in this four-dimensional world, the four-dimensional distance between any of these events should be something that all valid coordinate systems agree on. Our definition of symmetry then makes us ask the following question : What are the possible transformations that we can perform on the coordinates \( \left(t,x,y,z\right) \) such that we do not change the way in which we compute the four-dimensional length between any two events? Setting up this problem mathematically and carefully solving it gives us the answer. It turns out that there are three types of transformations that we can do to the coordinate system:
(A) Choose a direction, be it a direction in space or time. We can shift our coordinates (called ‘translation’) by any fixed amount \( a \). There four such independent translations that we can perform. Written mathematically:
\( \begin{align} \left(t,x,y,z\right)&\mapsto \left(t+a,x,y,z\right). \label{t-translation} \\ \left(t,x,y,z\right)&\mapsto \left(t,x+a,y,z\right). \label{x-translation} \\ \left(t,x,y,z\right)&\mapsto \left(t,x,y+a,z\right). \label{y-translations} \\ \left(t,x,y,z\right)&\mapsto \left(t,x,y,z+a\right). \label{z-translations} \end{align} \)
Obviously, in a universe which is infinitely big and empty, moving in any direction does not change how it looks, and in particular distances between ‘points’ will remain the same.
(B) We can rotate our spatial coordinates by any amount we wish. Any such rotation can be constructed out of the following three:
\( \begin{align} \left(t,x,y,z\right)&\mapsto\left(t,x\text{cos}(\theta)+y\text{sin}(\theta),-x\text{sin}(\theta)+y\text{cos}(\theta),z\right). \\ \left(t,x,y,z\right)&\mapsto\left(t,x,y\text{cos}(\theta)+z\text{sin}(\theta),-y\text{sin}(\theta)+z\text{cos}(\theta)\right). \\ \left(t,x,y,z\right)&\mapsto\left(t,-x\text{sin}(\theta)+z\text{cos}(\theta),y,z\text{cos}(\theta)+x\text{sin}(\theta) \right). \end{align} \)
Naturally, a universe which is empty and infinitely big, no matter what direction you look at, it will still look like an empty and infinitely big universe with the same concept of ‘distance’.
(C) We can choose a spatial direction and move along it at a constant velocity \( v \). It turns out this has the following mathematical formulation:
\( \begin{align} \left(t,x,y,z\right) & \mapsto \left( \gamma \left( t+\frac{vx}{c^{2}} \right), \gamma (x+vt), y, z \right). \\ \left(t,x,y,z\right) & \mapsto \left( \gamma \left( t+\frac{vy}{c^{2}} \right), x, \gamma (y+vt), z \right). \\ \left(t,x,y,z\right) & \mapsto \left( \gamma \left( t+\frac{vz}{c^{2}} \right), x, y, \gamma (z+vt) \right). \end{align} \)
where
\( \gamma = \frac{1}{\sqrt{1-v^{2}/c^{2}}}\).
The final three transformations come from something called the principle of relativity, which states that the laws of physics are the same in all inertial reference frames (which just means that whether you stand still or move at a constant velocity with respect to a certain experiment, the physics does not change). The appearance of \( c \) (the speed of light) is a special quirk of relativity; its presence in the formula has the consequence that one cannot exceed the speed of light.
This collection of 10 possible coordinate transformations which do not change the four-dimensional distance (called invariant length), plus all possible ways to combine them, form a group in the mathematical sense, a group called the Poincaré group. The specific universe which we considered here, the one governed purely by the special theory of relativity, is called Minkowski spacetime. Mathematically, what we just described can be stated as follows: ‘The Poincaré group is the isometry group of Minkowski spacetime’. (An isometry is just a symmetry that preserves the notion of distances and angles in spacetime).. This sentence provides the entire mathematical content of Einstein’s special theory of relativity.
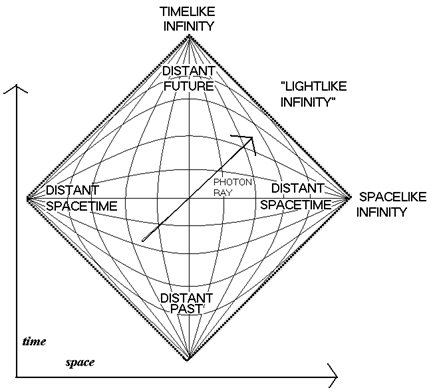
Physicists have a very useful way of representing all of Minkowski space in a single diagram, called the Penrose diagram. This diagram works by compressing infinity into a finitely small area (the diagram) using the mathematics of ‘conformal compactifications’. An important property of such a diagram is that light rays in it travel at \( 45^{\circ} \) angles. This diagram will prove to be helpful later on.
Ten years after coming up with the special theory of relativity, Einstein created the general theory of relativity (or ‘GR’ for short). The whole point of GR is that in the presence of gravity, spacetime is no longer Minkowski. In fact, in GR, gravity is identified with curvature of spacetime (while Minkowski spacetime has zero curvature). According to GR, whenever you add matter to the universe, this matter curves spacetime around it. Motion through this curvature is what we perceive as gravity. In such curved spacetimes, there is no a priori reason for the 10 symmetries of the Poincaré group to hold. In fact, in general, curved spacetimes have no symmetries at all. Mathematically speaking, curved spacetimes in general have no isometries.
So, if we define symmetry transformations as those coordinate transformations that leave lengths and angles invariant in spacetime, then it seems that in the presence of gravity, there are no symmetries. (As an aside: the statement here is that spacetime in these cases has no symmetries. In Silvester Borsboom’s recent article, you can read that the underlying theory still has many interesting symmetries.) What now? Do we abandon the notion of spacetime symmetries in the context of gravity? In physics, we have learned that symmetries greatly help organize our problems and even help us find the answers. So we wish to retain the notion of symmetry as much as possible, even if it is a slightly different notion than the one considered before.
To help us in developing a useful notion of gravitational symmetries, we make the following useful observation: Gravity is a force which weakens with distance. This is something that GR has in common with Newtonian gravity. Just like in Newton’s description of gravity the force weakens as an inverse power of distance, in GR going away from gravitating matter weakens the curvature of spacetime. So, as long as all the matter in the universe is localized to some finite region, it is possible to go far away from that matter such that there is no detectable force of gravity. At such a faraway distance, spacetime looks more and more like Minkowski space. Any universe where going far away from matter makes things seem more like Minkowski spacetime is called an ‘asymptotically flat spacetime’ (AFS). And we surely know how to analyse Minkowski spacetime. This allows us to come up with a new notion of symmetries, to be applied whenever you have gravity in the game. Here is the recipe:
(1) Take a universe with gravity and choose coordinates on such a spacetime.
(2) Write down the GR description of such a spacetime. This includes writing down what we mean by distances and angles on this space (mathematically, this is encapsulated by something called the ‘metric tensor’) and how the values for these things change as matter-induced curvature changes. The job of describing all this is the job of Einstein’s equations of GR.
(3) Move as far possible from all matter. Mathematically, this means approaching the ‘boundary’ of spacetime. In actual spacetime, this ‘boundary’ is infinitely far away, but in terms of the Penrose diagram given above, it actually means going to the diagonal borders of the diagram. As one approaches such a boundary, the universe starts looking more and more like Minkowski space.
(4) Then, consider all possible coordinate transformations which do not affect lengths and angles.
Before we go on to describe this group of transformations associated with asymptotically flat spacetimes, we must first face an issue that exists in following this procedure. The issue comes in the last step where we analyse all possible coordinate transformations. This is a tricky thing to do in GR. The foundational principle of GR is that physics is unchanged under change of coordinates. Everything is written down in a language where coordinate changes become redundant. Mathematically, we say that changes of coordinates act like ‘gauge transformations’ of gravity. Being physics enthusiasts, the readers probably know that gauge transformations are by definition, redundancies of the description of a system – see another recent article, by Pim van den Heuvel, for more details on this. To provide an analogy, these coordinate transformations of GR are analogous to the local phase transformations of an electromagnetic gauge theory.
Now we have a problem. If changes of coordinates are gauge transformations, nothing more than mere redundancies of description, then how do we interpret them as symmetries? The answer is a bit subtle. It turns out that not all transformations which look like gauge transformations are redundancies. It is possible to have symmetry transformations which have the mathematical form of gauge transformations but are in no way redundancies of the system. Understanding this takes one to the study of dynamical systems and the very definition of what dynamics consist of. This is perhaps a matter for another article. But, for now, all we need to know is the following fact: if a change of coordinates survives the journey to the boundary of spacetime, it has the potential to become an actual symmetry of the universe. Mathematically, this means that the function(s) that describe the change of coordinates must not go to zero at infinitely large distances.
Thus, we are given an updated recipe to come up with the symmetry of such a spacetime. We should follow steps 1 – 4 as outlined above, but we must add an extra 5th step at the end:
(5) Out of all these transformations, restrict attention to those which survive at the boundary of spacetime. The collection of all such transformations comprise a group which is called the ‘Asymptotic Symmetry Group’ (ASG) of the spacetime under consideration.
One possible criticism of this definition of symmetries might be as follows: if these symmetries are evaluated far, far away from all gravitating bodies, how do they help us in learning about those gravitating bodies? Actually, this is exactly where the advantage of using the notion of asymptotic symmetries lies. We can flip the question and realize the following fact: the gravitating system in the center of the universe can have an arbitrarily complex evolution through time. There can be coalescing black holes, exploding supernovae, orbiting planets etc. But far, far away from the system, the environment will still be gravity-less and therefore the asymptotic symmetries will remain the same.
Thus, these asymptotic symmetries, unchanging through the evolution of the gravitating system, can be used to impose order on the chaos of gravitational dynamics.
So, what are the asymptotic symmetries of asymptotically flat space? It turns out that if you go through the five-point process, you find that the group describing asymptotic symmetries is an infinitely big group called the ‘BMS group’. It contains the following transformations:
(A) It contains everything that the Poincaré group contains. Mathematically, the Poincaré group is a subgroup of the BMS group.
(B) It contains angle-dependent translations. Recall that in the Poincaré group, one translates everything in the universe by the same amount (an amount that was called ‘\( a \)’ in the equations above). In the BMS group, one is allowed to translate different points in spacetime by different amounts, with the differences captured by any arbitrary function of angles. Mathematically, the constant ‘\( a \)’ now becomes a function ‘\( a(\theta, \phi) \)’. These angle-dependent translations are described diagrammatically in the diagram below. In this Penrose diagram, you see how at the boundary of spacetime, different points can be translated by different amounts to the future.
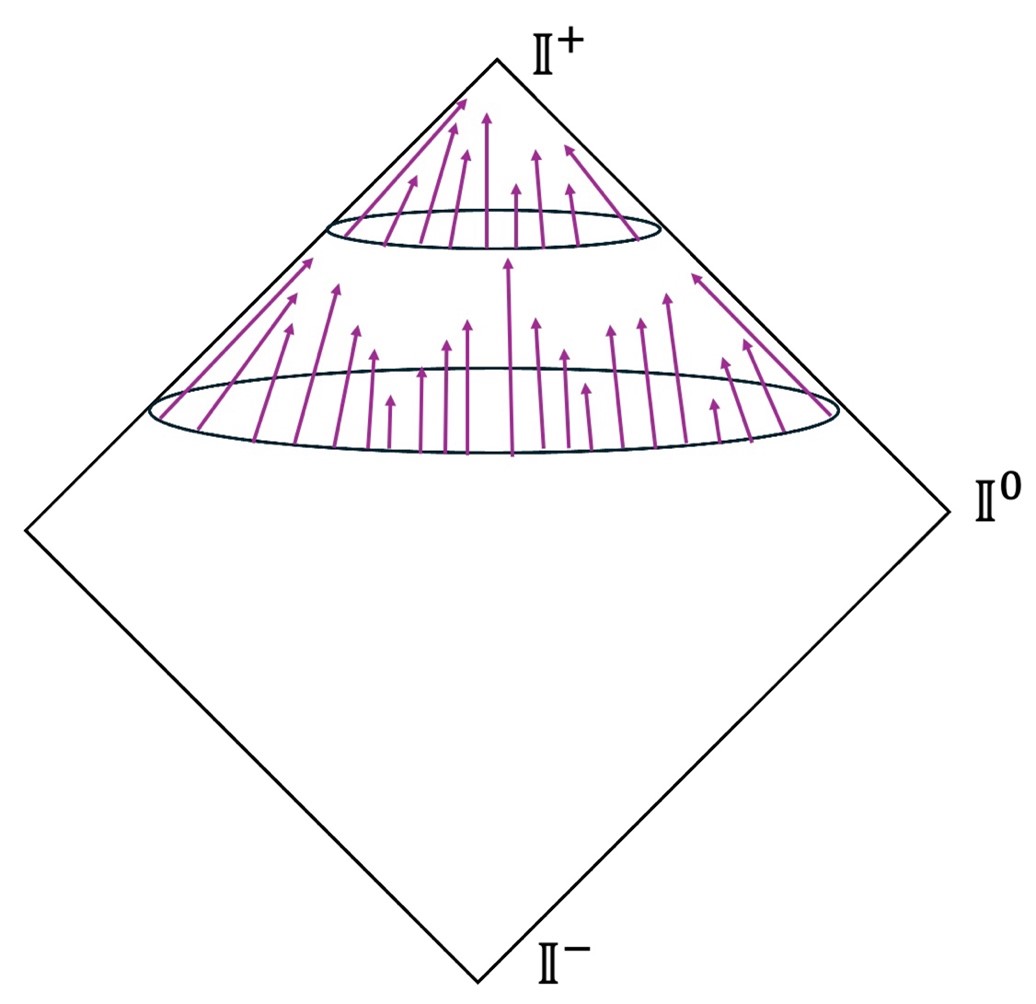
A fun fact: the name BMS comes from the initials of three physicists who initially worked on the subject of asymptotic symmetries: Bondi, Metzner and Sachs. However, there was a fourth physicist, a Dutch physicist with last name Van der Burg, who worked on the same subject and collaborated with some of the other authors. Still, for some reason, his name has not come to be associated with that of the group.
Now you know what asymptotic symmetries are. But what are they useful for? In recent years, asymptotic symmetries have proven useful in unearthing very deep relations between fields of physics which were previously thought to be unrelated. For example, asymptotic symmetries have allowed us to understand certain aspects of quantum field theory called ‘soft theorems’. This is because, by their very nature, asymptotic symmetries encode information about the universe on very large distances. In physics, large distances are naturally tied to small energies. Soft theorems form the aspect of quantum field theory which deals with very small energies. Previously, these soft theorems were thought of as just a fancy quirk of quantum field theories, while now we understand them on a much deeper level, due to asymptotic symmetries. A whole new field of quantum gravity called ‘Celestial Holography’ has developed over the last decade from the study of the BMS group and its relation to fields like quantum field theory, gravitational waves, etc. Moreover, asymptotic symmetries also seem to have strong implications for certain issues related to the black hole information paradox. Everything mentioned here is at the forefront of modern research!
Therefore, the concept of asymptotic symmetries not only allows us to describe classical gravity more elegantly, but it also allows us to tap into the quantum nature of our universe.